【信号分离】重叠非平稳信号的信号分解（Matlab实现）

原创已于 2024-11-01 09:14:41 修改 · 838 阅读

8 ·

CC 4.0 BY-SA版权

文章标签：

#matlab #开发语言

于 2024-11-01 09:03:39 首次发布

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

💥1 概述

一、背景与意义：在信号处理领域，常常会遇到重叠的非平稳信号。非平稳信号是指其统计特性随时间变化的信号，例如语音信号、生物医学信号、机械振动信号等。当多个非平稳信号重叠在一起时，直接分析这些信号变得非常困难。因此，对重叠非平稳信号进行信号分解具有重要的现实意义。信号分解可以将复杂的重叠信号分离成多个相对简单的成分，有助于更好地理解信号的本质特征、提取有用信息、进行故障诊断、模式识别等任务。

二、主要方法：1. 小波变换：小波变换是一种常用的信号分解方法，它能够在不同尺度上对信号进行分析。对于非平稳信号，小波变换可以有效地捕捉信号的时频特性，将信号分解为不同频率和时间分辨率的子信号。 2. 经验模态分解（EMD）及变体：EMD 方法可以自适应地将信号分解为一系列固有模态函数（IMF）。这些 IMF 反映了信号在不同时间尺度上的局部特征。变体如集合经验模态分解（EEMD）等在一定程度上改善了 EMD 的一些局限性。 3. 变分模态分解（VMD）：VMD 是一种新的信号分解方法，它通过构建和求解变分问题，将信号分解为多个具有特定中心频率和有限带宽的模态分量。

三、挑战与难点： 1. 模态混叠：在一些信号分解方法中，可能会出现模态混叠现象，即不同的信号成分被错误地分配到同一个分解分量中，或者同一个信号成分被分配到多个分解分量中。 2. 噪声影响：实际信号中往往存在噪声，噪声会干扰信号分解的结果，使得分解后的信号难以准确反映原始信号的特征。 3. 计算复杂度：一些信号分解方法的计算复杂度较高，尤其是对于大规模数据或高维信号，可能需要较长的计算时间和较大的计算资源。

四、应用领域：1. 故障诊断：在机械工程中，通过对设备运行产生的振动信号进行分解，可以提取出故障特征，实现对设备故障的早期诊断。 2. 语音处理：对于重叠的语音信号，可以进行分解以分离不同说话人的声音，或者提取特定的语音特征用于语音识别等任务。 3. 生物医学信号处理：如对心电图、脑电图等生物医学信号进行分解，有助于分析生理状态、检测异常情况等。

📚2 运行结果

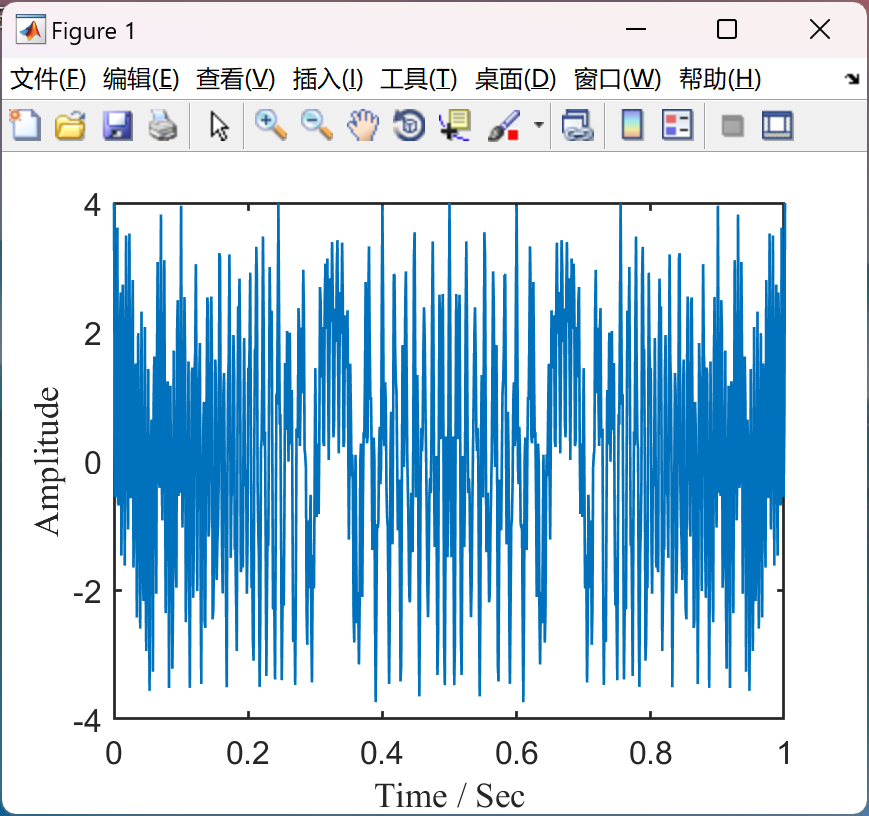
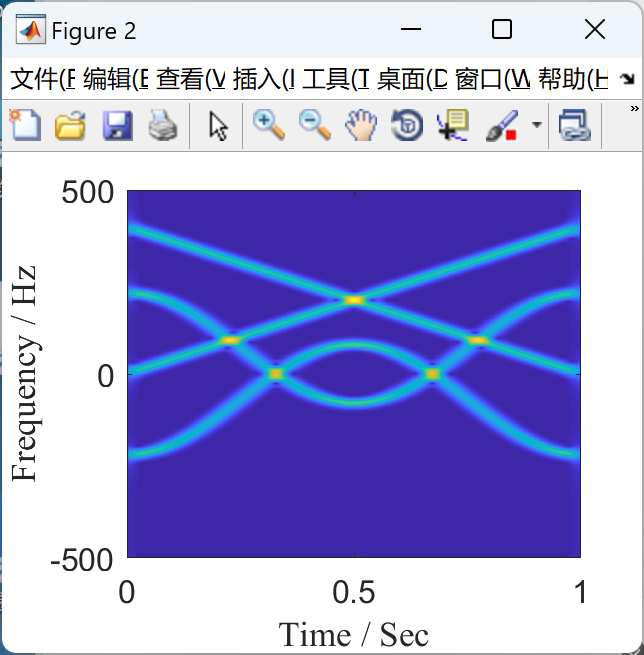
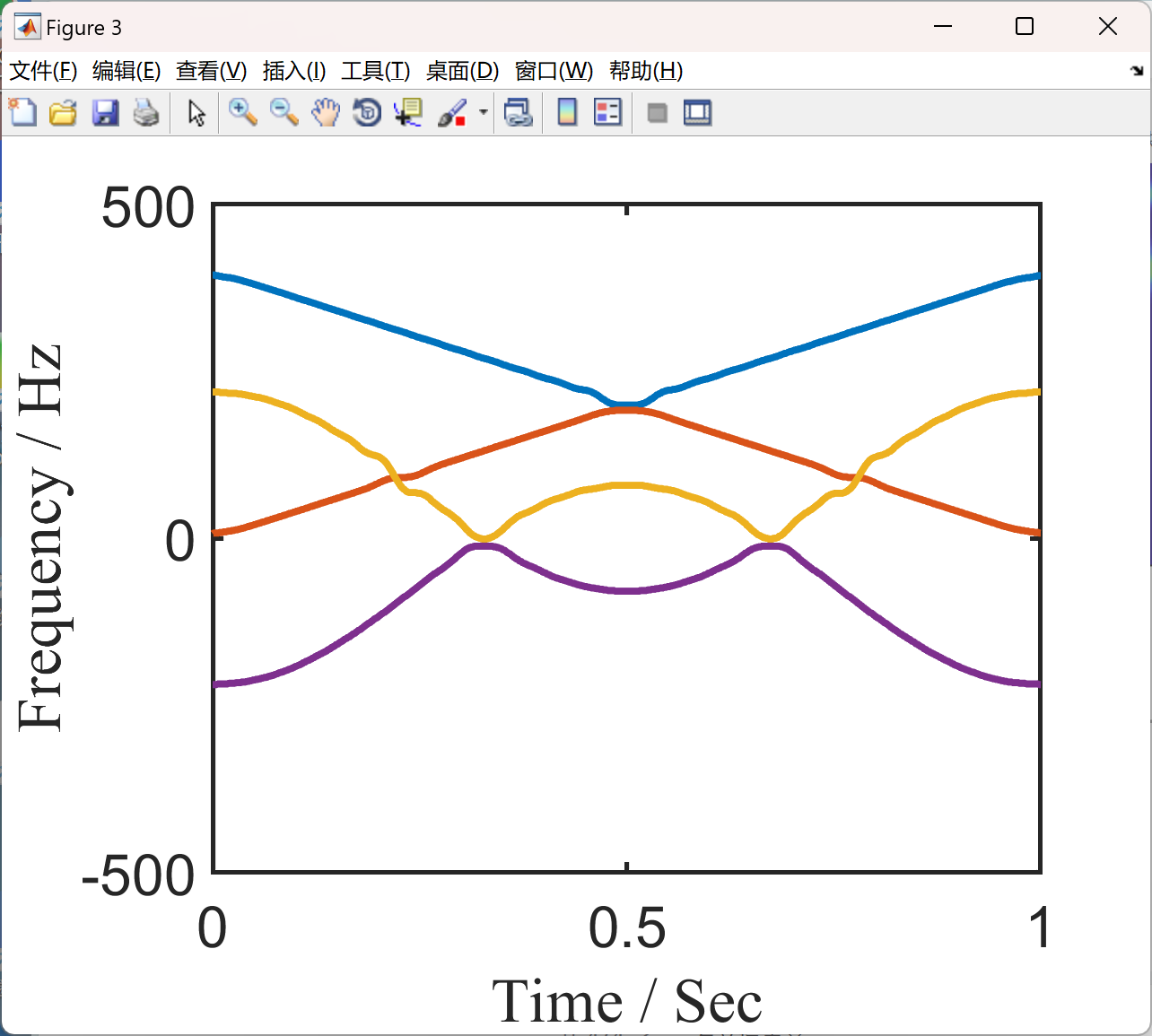
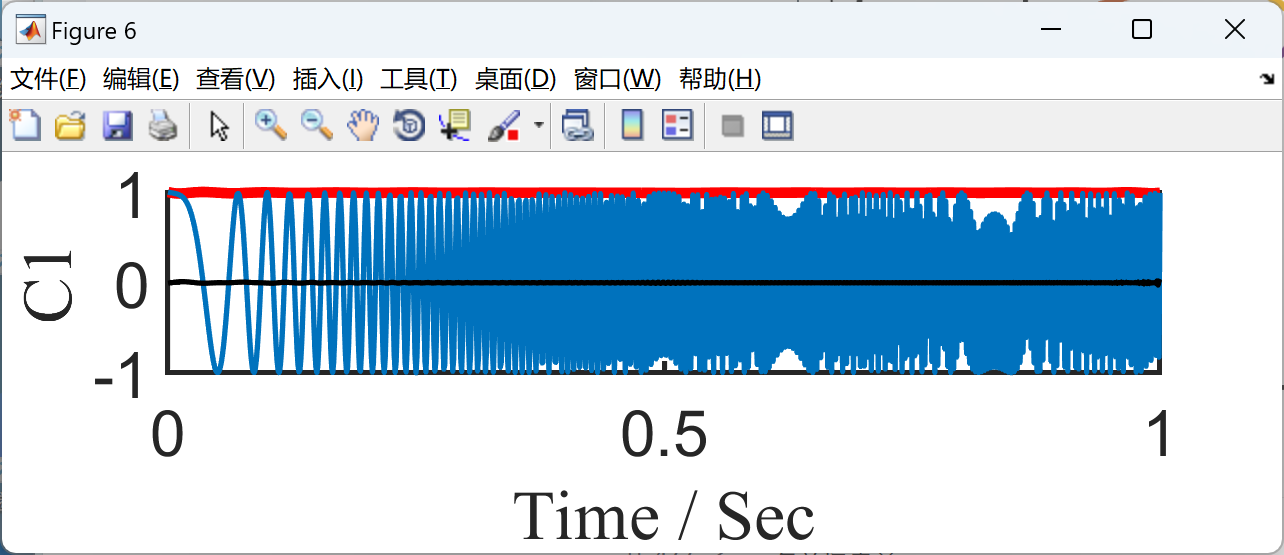
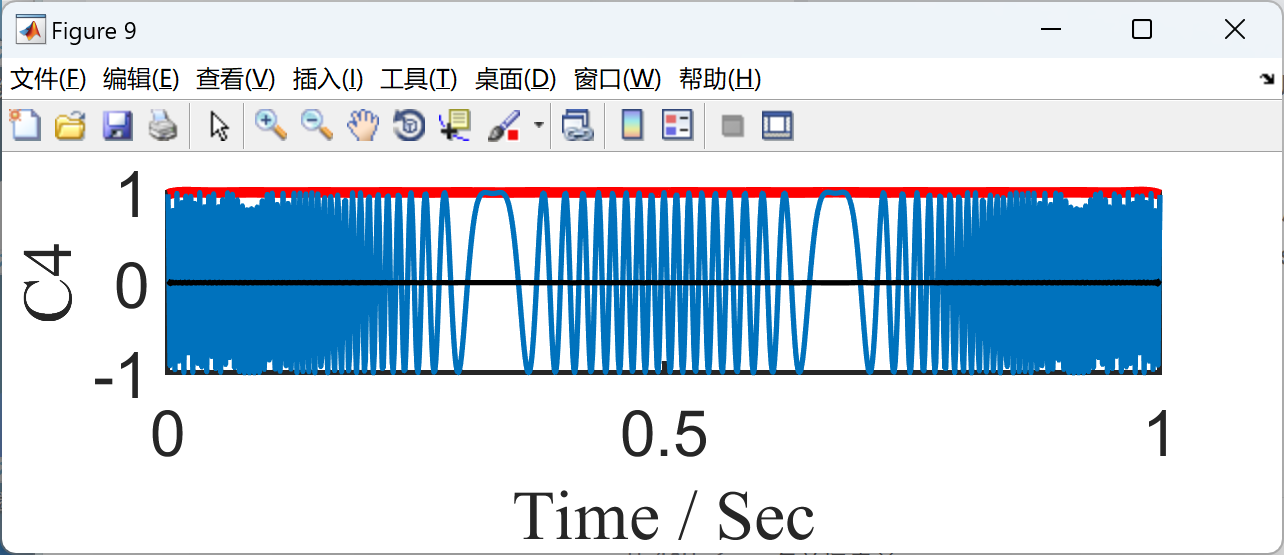
部分代码：

function [Spec,f] = STFT(Sig,SampFreq,N,WinLen);

if (isreal(Sig))
Sig = hilbert(Sig);
end

SigLen = length(Sig);


WinLen = ceil(WinLen / 2) * 2;%对窗函数长度圆整变为偶数
t = linspace(-1,1,WinLen)';%窗函数时间是在正负1s之间，
sigma = 0.28;
WinFun = (pi*sigma^2)^(-1/4)*exp((-t.^2)/2/(sigma^2));

Lh = (WinLen - 1)/2; %取窗宽的一半

Spec = zeros(N,SigLen) ;  

for iLoop = 1:SigLen,
    
    tau = -min([round(N/2)-1,Lh,iLoop-1]):min([round(N/2)-1,Lh,SigLen-iLoop]);
    temp = floor(iLoop + tau);
    temp1 = floor(Lh+1+tau);
    rSig = Sig(temp);

    rSig = rSig .* conj(WinFun(temp1));
    Spec(1:length(rSig),iLoop) = rSig;
end;

Spec = fftshift(fft(Spec),1); %计算矩阵的傅里叶变换，并用fftshift

[nLevel, SigLen] = size(Spec);

f = linspace(-SampFreq/2,SampFreq/2,nLevel);
t = (0: SigLen-1)/SampFreq;