【信号分离】用维纳滤波进行信号分离（Matlab实现）

荧光Matlab

已于 2024-11-02 21:30:52 修改

阅读量823

点赞数 22

CC 4.0 BY-SA版权

文章标签： matlab 开发语言

于 2024-11-01 09:18:37 首次发布

本文链接：https://blog.youkuaiyun.com/Matlab88888/article/details/143423192

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

💥1 概述

一、背景与意义：在信号处理中，常常需要从复杂的混合信号中分离出特定的信号成分。维纳滤波作为一种经典的信号处理方法，在信号分离方面发挥着重要作用。它可以有效地从被噪声污染的信号中恢复出原始信号，或者将多个混合的信号分离成各自独立的成分，这对于提高信号的质量、提取有用信息以及解决实际应用中的诸多问题具有重大意义。

二、基本原理：维纳滤波基于最小均方误差准则。它通过对输入信号的统计特性进行分析，设计一个滤波器，使得滤波后的输出信号与期望信号之间的均方误差最小。在信号分离的应用中，通常假设混合信号是由多个独立的源信号经过线性混合得到的，并且已知或可以估计出混合系统的某些统计特性。维纳滤波利用这些信息来构建一个逆滤波器，以尽可能地恢复出原始的源信号。

三、主要步骤：1. 信号建模：确定混合信号的生成模型，例如线性混合模型。明确源信号的特性以及混合过程的方式。 2. 统计特性估计：估计混合信号的自相关函数、互相关函数等统计特性。这些统计信息对于设计维纳滤波器至关重要。 3. 滤波器设计：根据估计的统计特性，设计维纳滤波器。确定滤波器的参数，使得滤波器能够在最小均方误差意义下实现信号分离。 4. 信号分离：将混合信号输入到设计好的维纳滤波器中，得到分离后的信号估计。

四、应用领域： 1. 通信系统：在无线通信中，用于分离多径传播引起的混合信号，提高通信质量。 2. 音频处理：分离语音信号和背景噪声，改善语音的清晰度和可懂度。 3. 图像恢复：从模糊或噪声污染的图像中分离出原始图像，提高图像质量。 4. 生物医学信号处理：分离生物医学信号中的不同成分，如心电图中的不同波形等。

📚2 运行结果

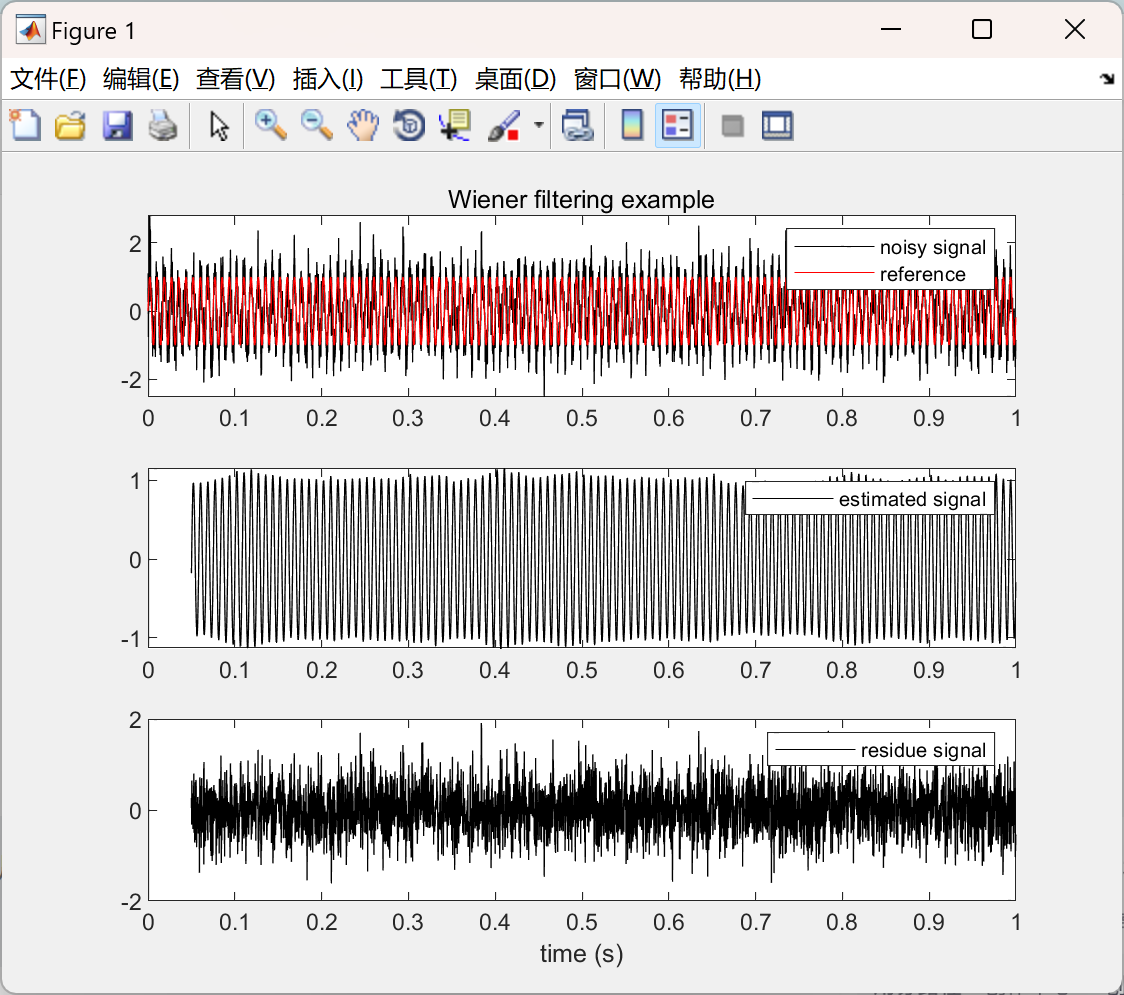
主函数部分代码：


clear
close all
clc
fs = 4000; % sampling frequency
T = 1;% total recording time
L = T .* fs; % signal length
tt = (0:L-1)/fs; % time vector
ff = (0:L-1)*fs/L;
y = sin(2*pi*120 .* tt); y = y(:); % reference sinusoid
x = 0.50*randn(L,1) + y; x = x(:); % sinusoiud with additive Gaussian noise
N = 200; % filter order
[xest,b,MSE] = wienerFilt(x,y,N);
% plot results
figure
subplot(311)
plot(tt,x,'k'), hold on, plot(tt,y,'r')
title('Wiener filtering example')
legend('noisy signal','reference')
subplot(312)
plot(tt(N+1:end),xest,'k')
legend('estimated signal')
subplot(313)
plot(tt(N+1:end),(x(N+1:end) - xest),'k')
legend('residue signal')