一种用于多层设施布局问题的混合式Dantzig-Wolfe分解算法（Matlab代码实现）

 💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

---

💥1 概述

文献

摘要：多层设施布局问题（MFLP）是最重要和复杂的设施布局问题之一，在制造和服务行业的设施设计中有许多应用。本研究首次提出了一种混合式Dantzig-Wolfe分解算法来解决MFLP问题。提出的解决方案分为两个步骤。在第一步中，应用数学公式将部门分配到不同楼层，使得物料流量较高的部门位于同一楼层或相邻楼层。在第二步中，考虑第一步的输出，将MFLP分解为一个主问题和一些子问题，形成Dantzig-Wolfe分解算法，分别找到每个楼层的最佳布局。然后轻松形成多个楼层的综合布局。提出的算法使用文献中的一些示例问题和一些新生成的测试问题进行评估。获得的结果显示，与文献中的方法相比，提出的算法具有更高的优越性。

关键词：多层设施布局问题、Dantzig-Wolfe分解算法、Bender分解算法、NP难问题

📚2 运行结果

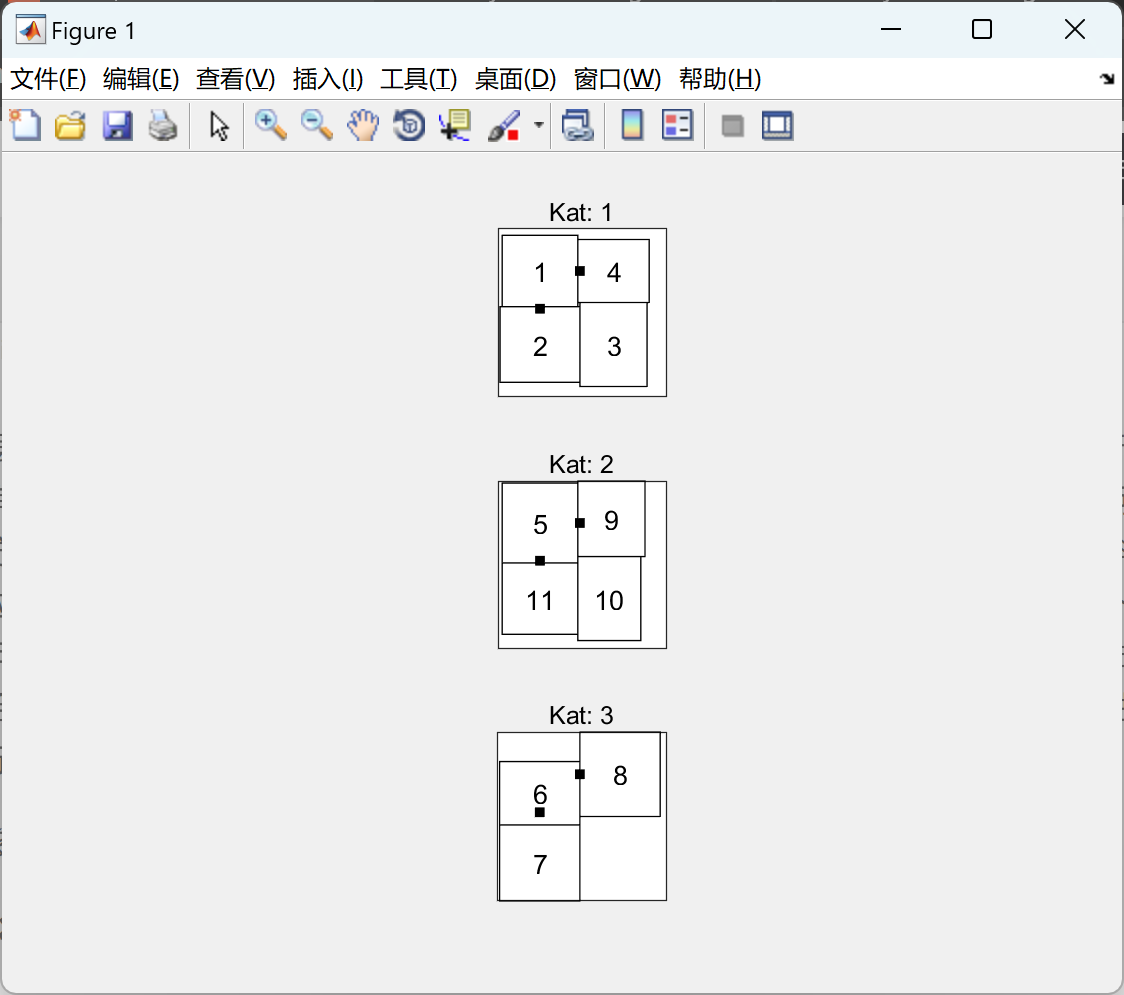
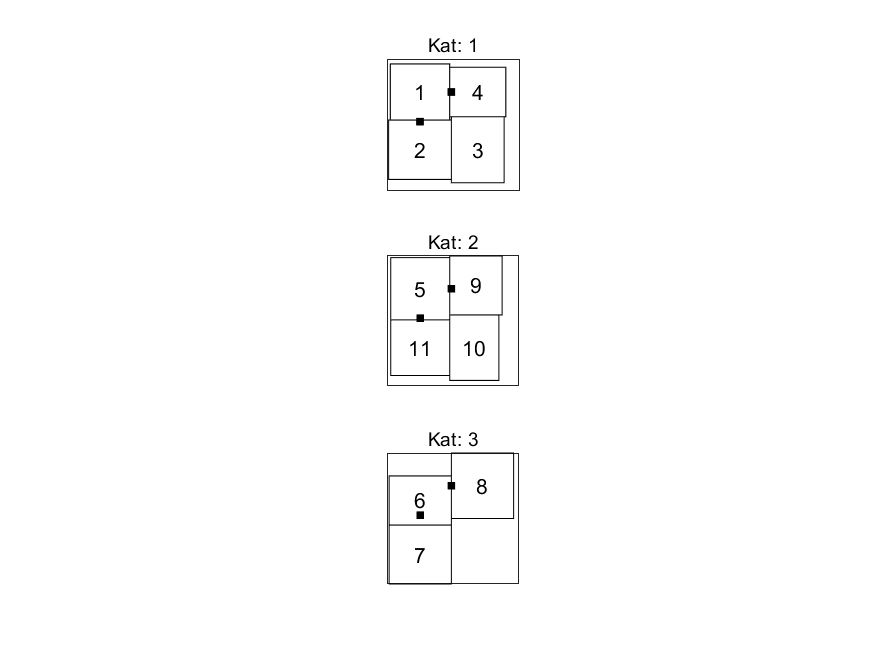
部分代码：

function [xdantzig,ydantzig] = plotAllFloors(x_DanWof,kat,lx,ly,Lx,Ly,xe,ye,K,Nk,Ne,ind,fval,p1,p2,reverse)
count = 0; xf=[]; yf=[]; kkk = [];
Le = min(Lx,Ly)/40;
figure;
for k = 1:K
    xxx = x_DanWof(count+[1:4*Nk(k)^2+2*(1+Ne)*Nk(k)]);
    
    count = count + 4*Nk(k)^2+(2+2*Ne)*Nk(k);
    lxk = lx(kat == k);
    lyk = ly(kat == k);
    xdantzig(kat==k) = xxx(1:Nk(k));
    ydantzig(kat==k) = xxx(1+Nk(k):2*Nk(k));
    
    subplot(p1,p2,k); xlim([0 Lx]); ylim([0 Ly]);
    title(['Kat: ' int2str(k)]); pbaspect([Lx Ly 1]);
    for i = 1:Nk(k)
        rectangle('position',[xxx(i)-lxk(i) xxx(Nk(k)+i)-lyk(i) 2*lxk(i) 2*lyk(i)]);
        text(xxx(i),xxx(Nk(k)+i),num2str(ind{k}(i)),'HorizontalAlignment','center');
    end
    for i = 1:Ne
        rectangle('position',[xe(i)-Le ye(i)-Le 2*Le 2*Le],'FaceColor',[0 0 0]);
    end
    set(gca,'YTick',[],'XTick',[],'Box','on')
    if reverse
        set(gca,'YDir','reverse');
    end
end
try
    sgtitle({'Dantzig-Wolfe Optimization',['fval = ' num2str(fval)]});
    disp(['Dantzig-Wolfe Optimization: fval = ' num2str(fval)])
catch
    disp(['Dantzig-Wolfe Optimization: fval = ' num2str(fval)])
end
end

🎉3 参考文献

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。

🌈4 Matlab代码实现