不确定性感知轨迹规划：利用不确定性量化和传播在移动机器人可穿越性预测中的应用研究（Matlab代码实现）

 💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码、数据

---

💥1 概述

文献来源：

Uncertainty-Aware Trajectory Planning: Using Uncertainty Quantification and Propagation in Traversability Prediction of Planetary Rovers | IEEE Journals & Magazine | IEEE Xplore

Uncertainty-Aware Trajectory Planning: Using Uncertainty Quantification and Propagation in Traversability Prediction of Planetary Rovers - 百度学术

摘要：在极端环境中，如火星或火山地区，移动机器人已被用于科学任务，或作为未来载人任务的前导。这种名为a的机器人由航天合格、辐射硬化和低时钟的机载计算机管理，并自主地在具有挑战性的地形上行驶。

关键词：不确定性 预测模型 机器人 轨迹规划 轮子 反应动力

📚2 运行结果

 

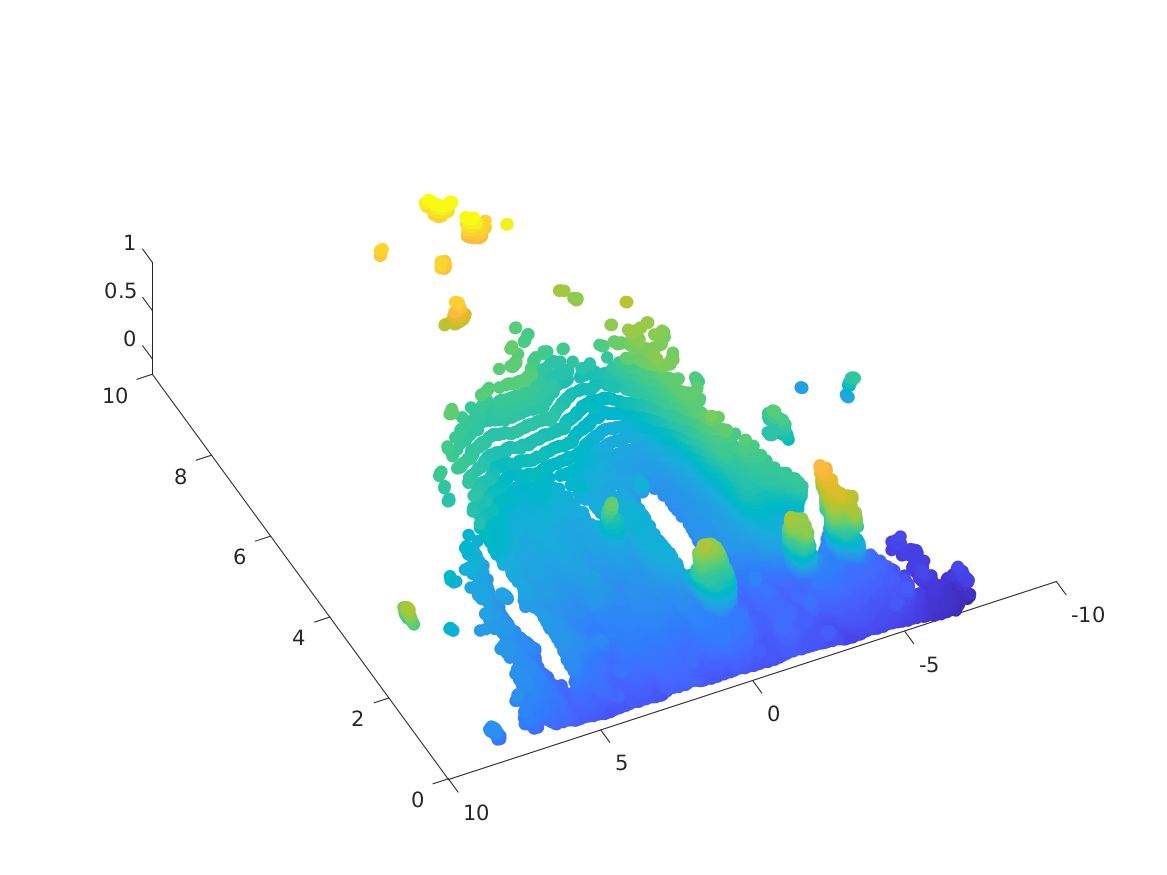
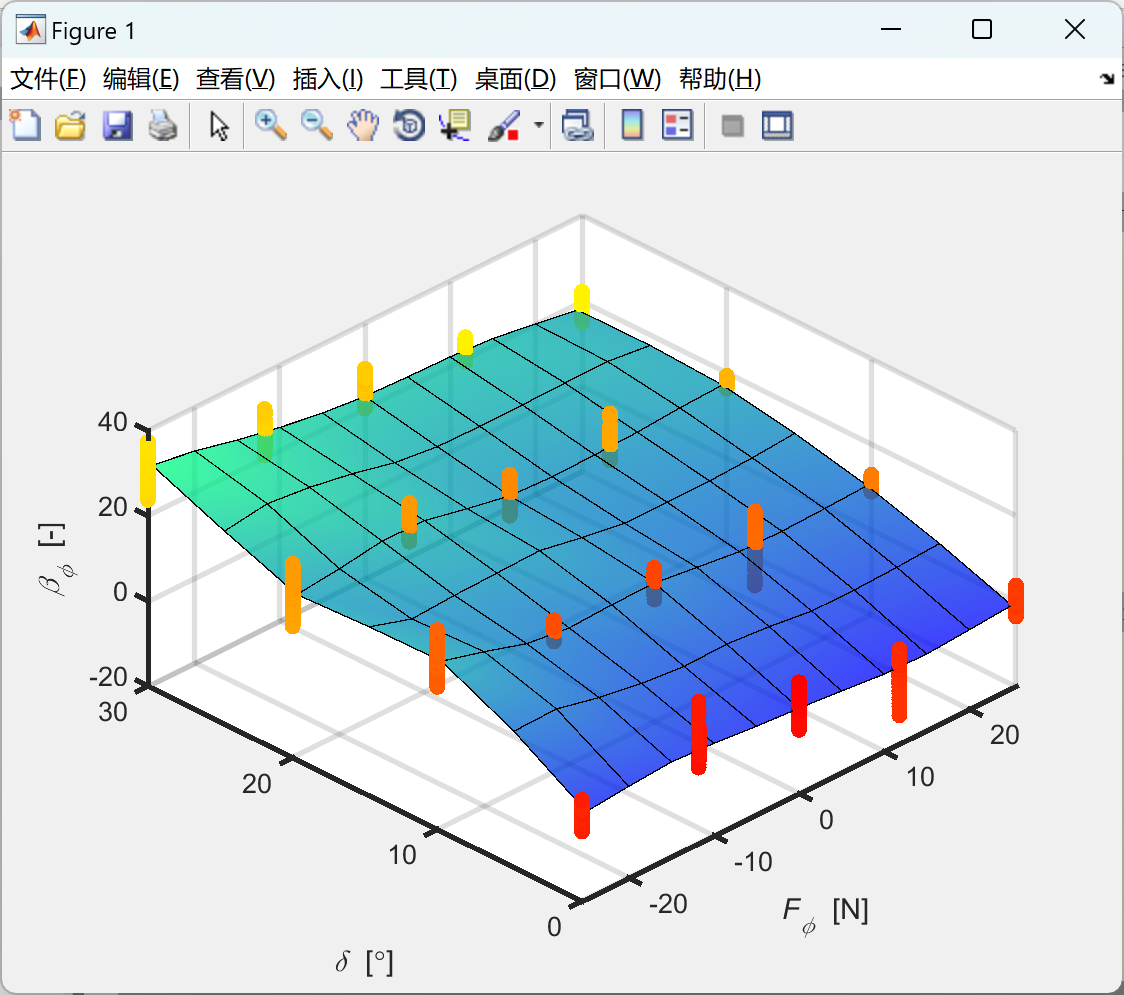
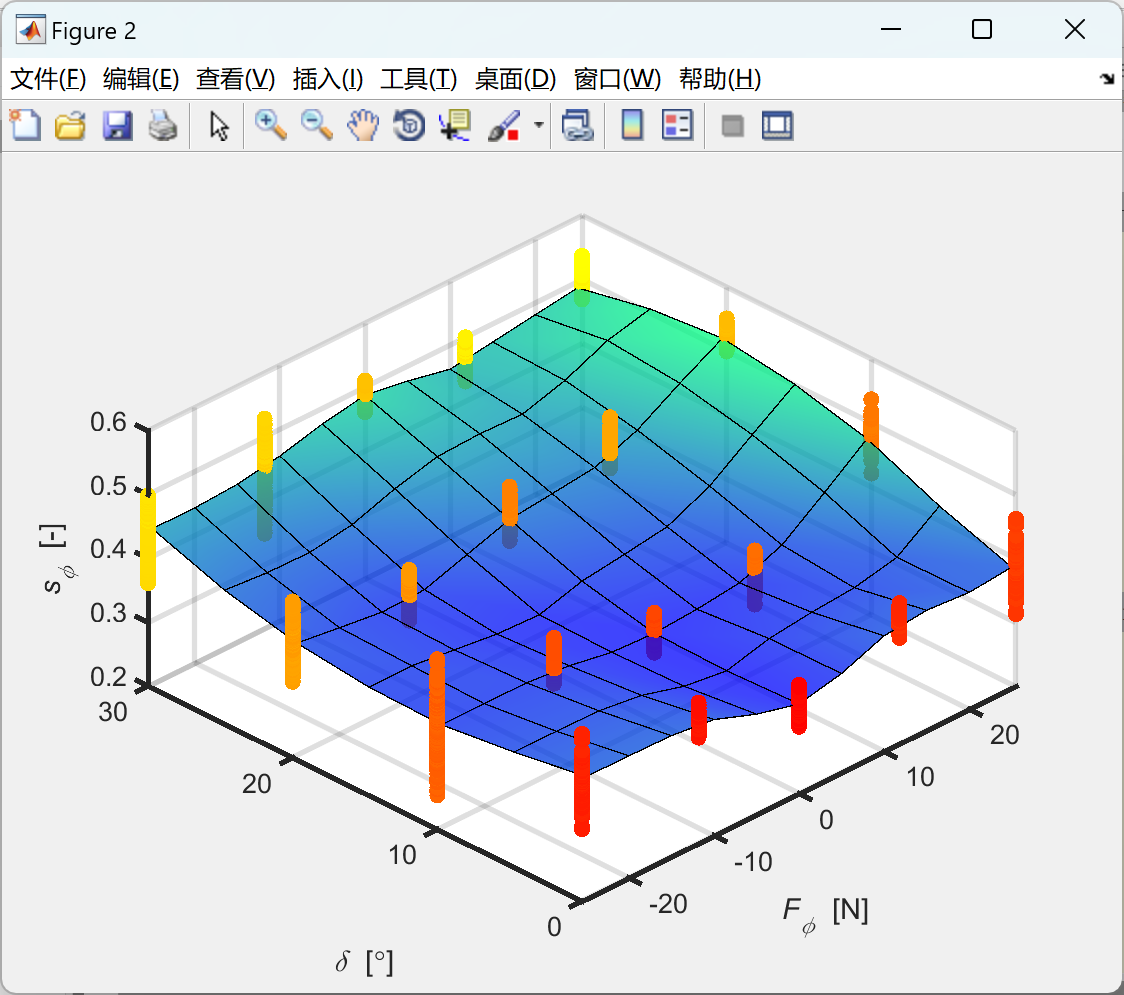
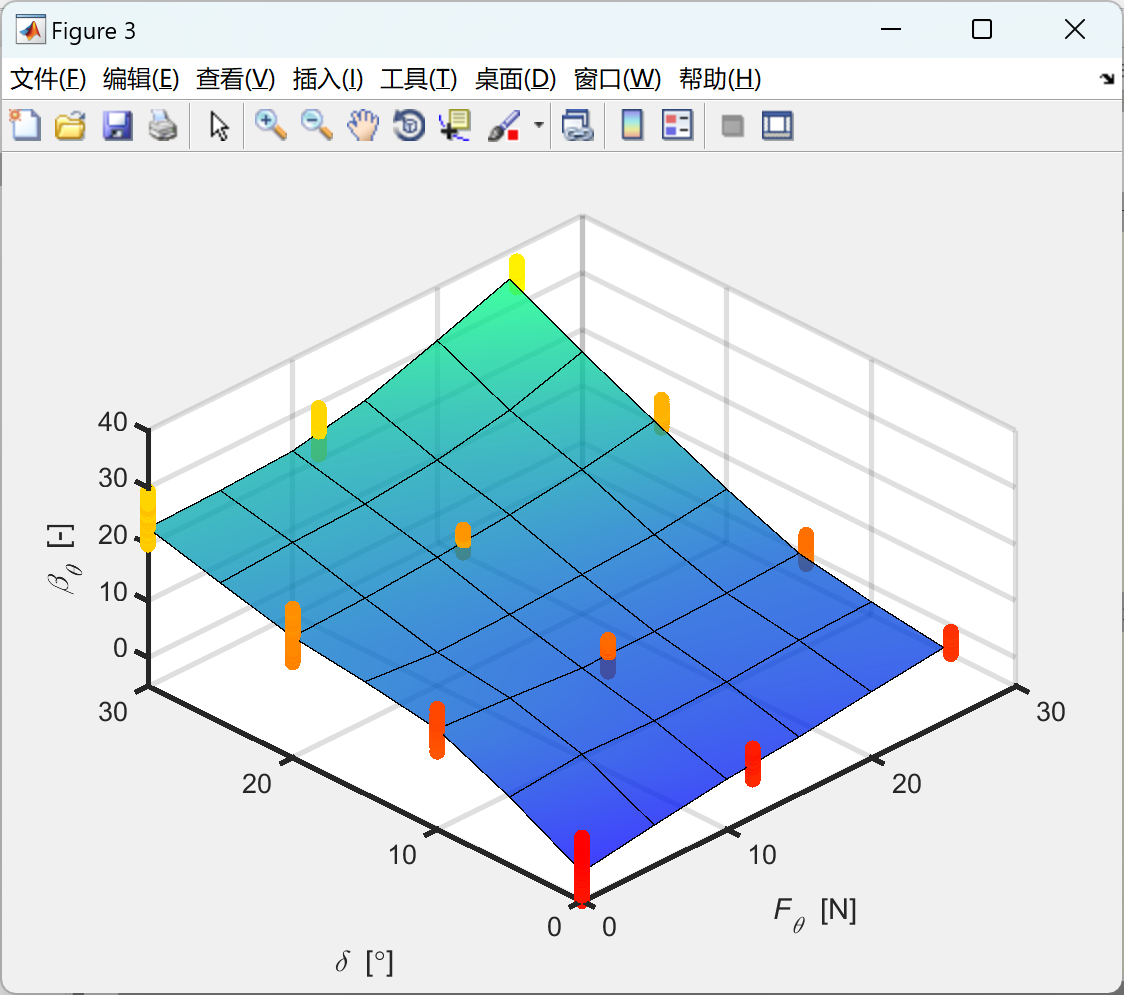
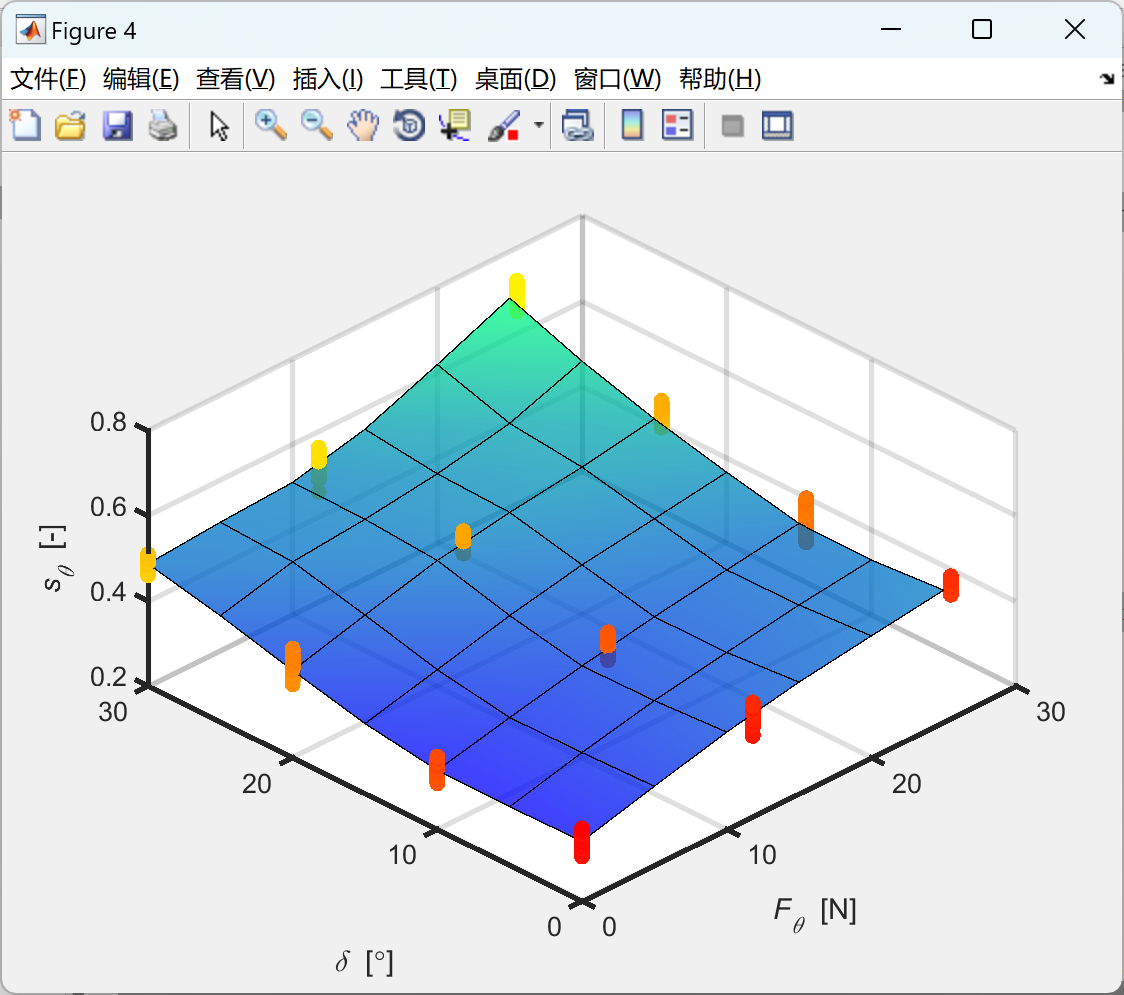
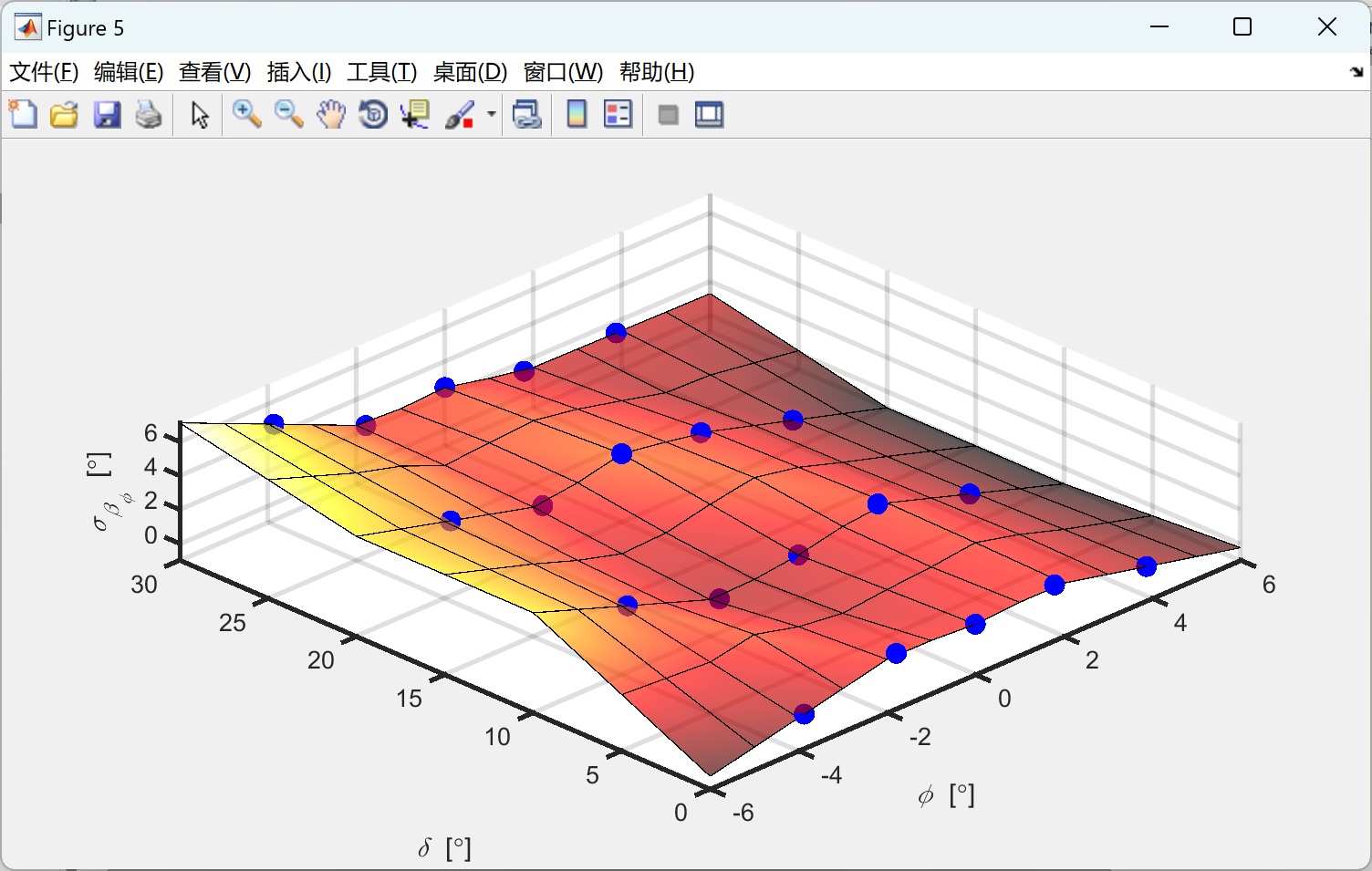
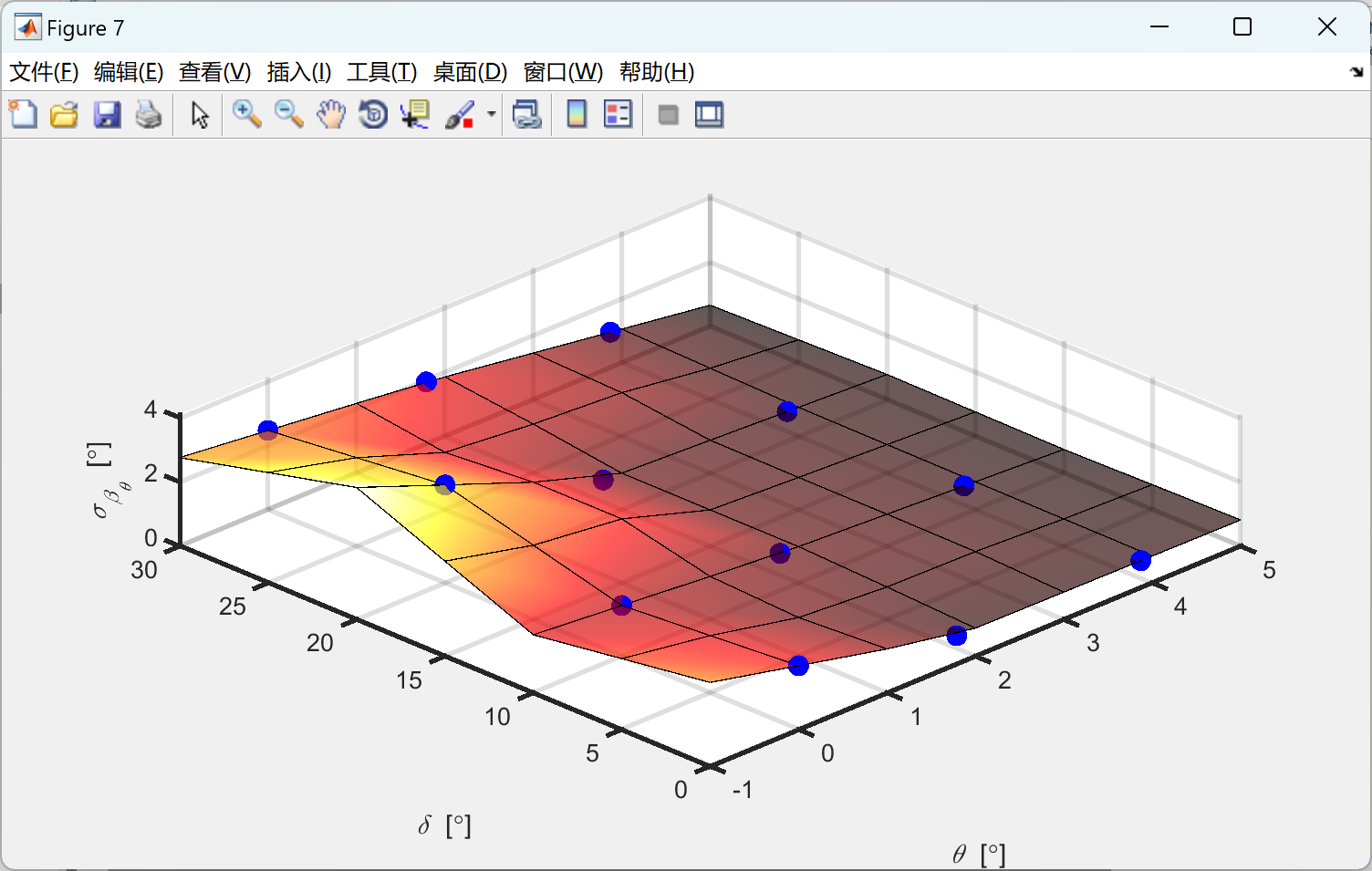
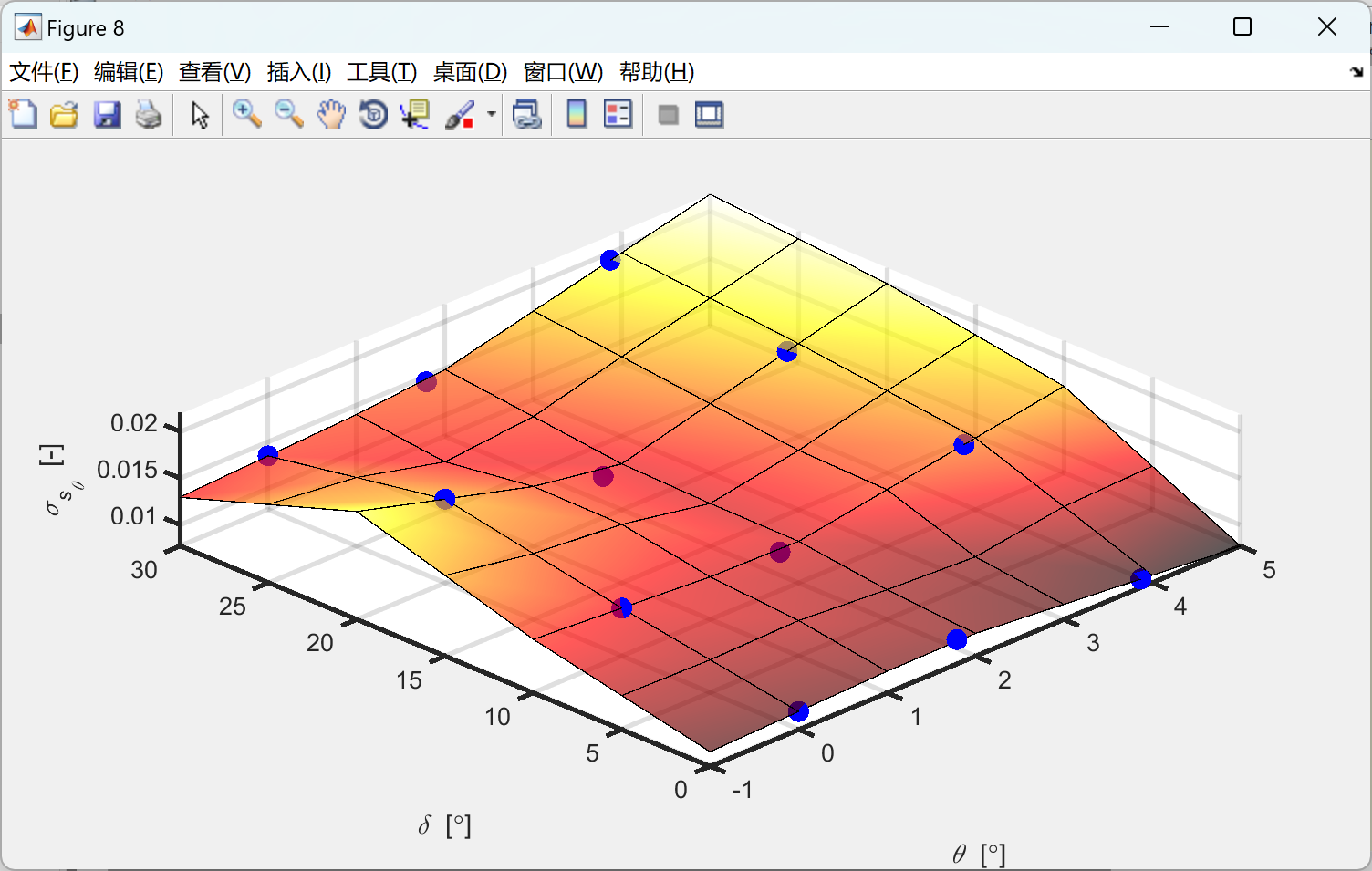
部分代码：

% plot and interpolate
F_phi_range = -25:5:25;
F_theta_range = 0:5:25;
plot_slip_data(delta_phi, F_phi, s_phi, '\it F_\phi \rm [N]', '\it{s_\phi} \rm [-]', F_phi_range, 'Fphi_vs_s');
plot_slip_data(delta_theta, F_theta, s_theta, '\it F_\theta \rm [N]', '\it{s_\theta} \rm [-]', F_theta_range, 'Ftheta_vs_s');
plot_slip_data(delta_phi, F_phi, beta_phi, '\it F_\phi \rm [N]', '\it{\beta_\phi} \rm [-]', F_phi_range, 'Fphi_vs_beta');
plot_slip_data(delta_theta, F_theta, beta_theta, '\it F_\theta \rm [N]', '\it{\beta_\theta} \rm [-]', F_theta_range, 'Ftheta_vs_beta');

% sigma calculation
sigma_s_phi = [];
sigma_s_theta = [];
sigma_b_phi = [];
sigma_b_theta = [];

data_size = 500;

for i=1:1:size(F_phi, 2)/data_size
    
    sigma_s_phi = horzcat(sigma_s_phi, std(s_phi(1+(i-1)*data_size:i*data_size)));
    sigma_b_phi = horzcat(sigma_b_phi, std(beta_phi(1+(i-1)*data_size:i*data_size)));
    
end

for i=1:1:size(F_theta, 2)/data_size
    
    sigma_s_theta = horzcat(sigma_s_theta, std(s_theta(1+(i-1)*data_size:i*data_size)));
    sigma_b_theta = horzcat(sigma_b_theta, std(beta_theta(1+(i-1)*data_size:i*data_size)));
    
end

sigma_s_phi
sigma_b_phi
sigma_s_theta
sigma_b_theta

function plot_slip_data(data_x, data_y, data_z, label_y, label_z, F_range, fig_name)
    delta_range = 0:5:30;
    
    figure()

    hold on;
    S = scatter3(data_x, data_y, data_z,'filled');

    C = autumn(numel(data_y));
    S.CData = C;
    hold on;

🎉3 参考文献

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。

[1] Takemura R , Ishigami G .Uncertainty-Aware Trajectory Planning: Using Uncertainty Quantification and Propagation in Traversability Prediction of Planetary Rovers[J].IEEE Robotics & Automation Magazine, PP[2024-01-28].DOI:10.1109/MRA.2023.3341289.

🌈4 Matlab代码、数据