【WFR滤波器】在时空频率域中的波场重建滤波的分析方法研究（Matlab代码实现）

 💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码及文章

---

💥1 概述

在大范围内传输物理声场时，需要将麦克风阵列接收的信号转换为扬声器阵列的驱动信号，以再现声场。我们提出了一种利用平面或线性麦克风和扬声器阵列进行信号转换的方法。基于时空频率域中波传播的物理方程，我们从理论上推导了连续变换方程。通过引入空间采样，得到了独特确定的变换滤波器，称为波场重建滤波器（WFR滤波器）。数值模拟表明，WFR滤波器可以实现与传统最小二乘（LS）方法获得的性能相同。然而，由于所提出的WFR滤波器被表示为空间卷积，它在滤波器设计、滤波器大小、计算成本和滤波器稳定性方面具有许多优势，胜过LS方法设计的变换滤波器。

声音的录制、传输和再现方式一直以来都是声学信号处理中的一个基本问题。为了在大范围内传输物理声场，录制和再现信号需要使用许多麦克风和扬声器，以及对这些信号进行转换。作者们专注于将麦克风接收的信号转换成扬声器的驱动信号，以便在麦克风和扬声器的排列是平面或线性时再现声场。已经提出了许多声场再现方法，可以计算扬声器的驱动信号，以再现所需的声场。为了实现使用麦克风和扬声器阵列的实时录制和再现系统，例如，电信系统，最好使用麦克风阵列获得的声压分布来计算驱动信号。这是因为除了声压之外，所需声场的任何参数，例如声源位置、方向和原始信号，都是未知的且难以获得。因此，直接将声压转换成驱动信号的方法是必要的。我们将这种类型的转换称为声压到驱动信号（SP-DS）转换。

基于球谐展开的方法，例如全方位声场（Ambisonics）[1]，可以通过编码和解码过程[2]–[6]来看作是SP-DS转换方法。然而，这些方法不能用于麦克风和扬声器的平面或线性阵列。

波场合成（WFS）[7]是一种基于Kirchhoff-Helmholtz积分或Rayleigh积分的声场再现方法，这是声波传播的物理方程。尽管提出了几种WFS的公式，但大多数不能用于SP-DS转换。WFS的原始公式将静态相位近似引入Rayleigh I积分[8]–[10]。因此，要再现的声源的参数被包括在驱动信号的函数中。Spors等人提出的另一种公式[11]包括声压梯度的平面或线性分布在驱动信号的函数中。由于普通麦克风阵列难以获取这些参数，这种方法不能用于SP-DS转换。Ahrens和Spors提出了用于平面或线性扬声器阵列的频谱分割方法[12]。详细讨论了本节中讨论的原因，这种方法不适合SP-DS转换。Ahrens和Spors提出的另一种方法[13]可以用作SP-DS转换的手段，当可以估计所需声场的球谐展开时。虽然基于波场分析的方法[14]或作者先前提出的方法[15]可以作为通过扩展WFS导出的SP-DS转换方法来应用，但必须引入自由场假设下的声场外推。详细文章见第4部分。

📚2 运行结果

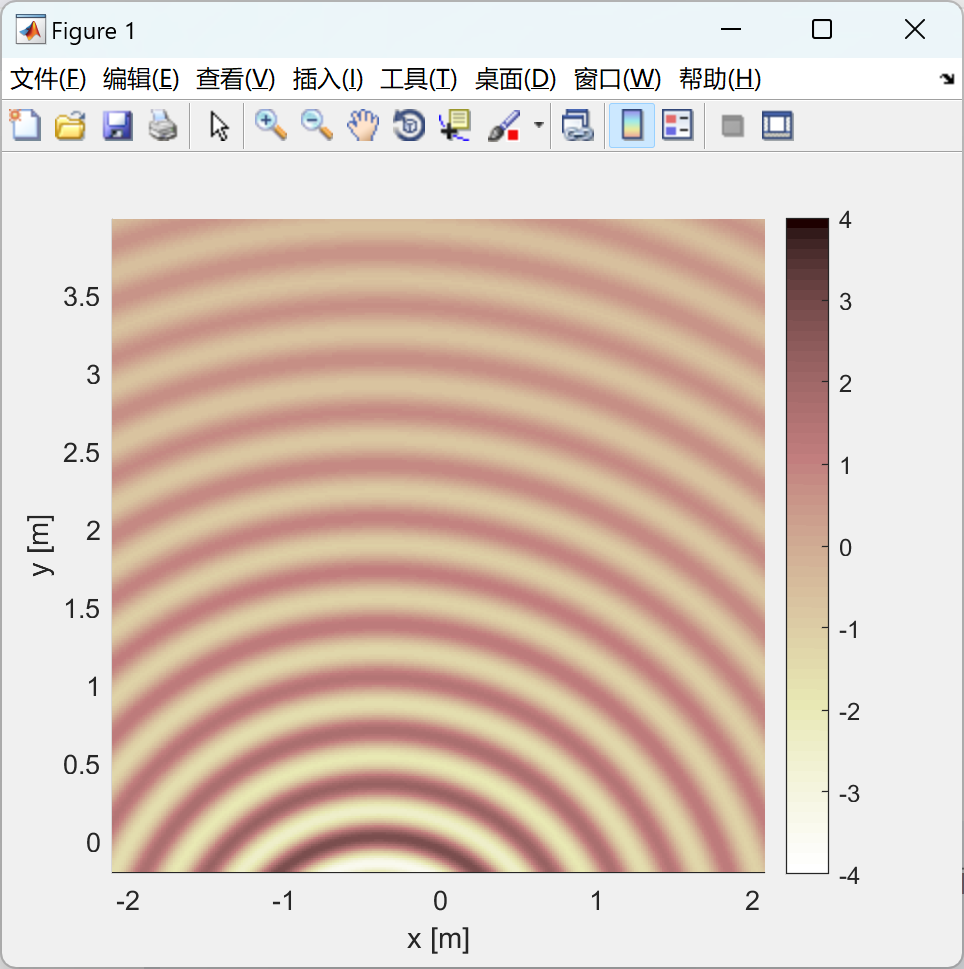
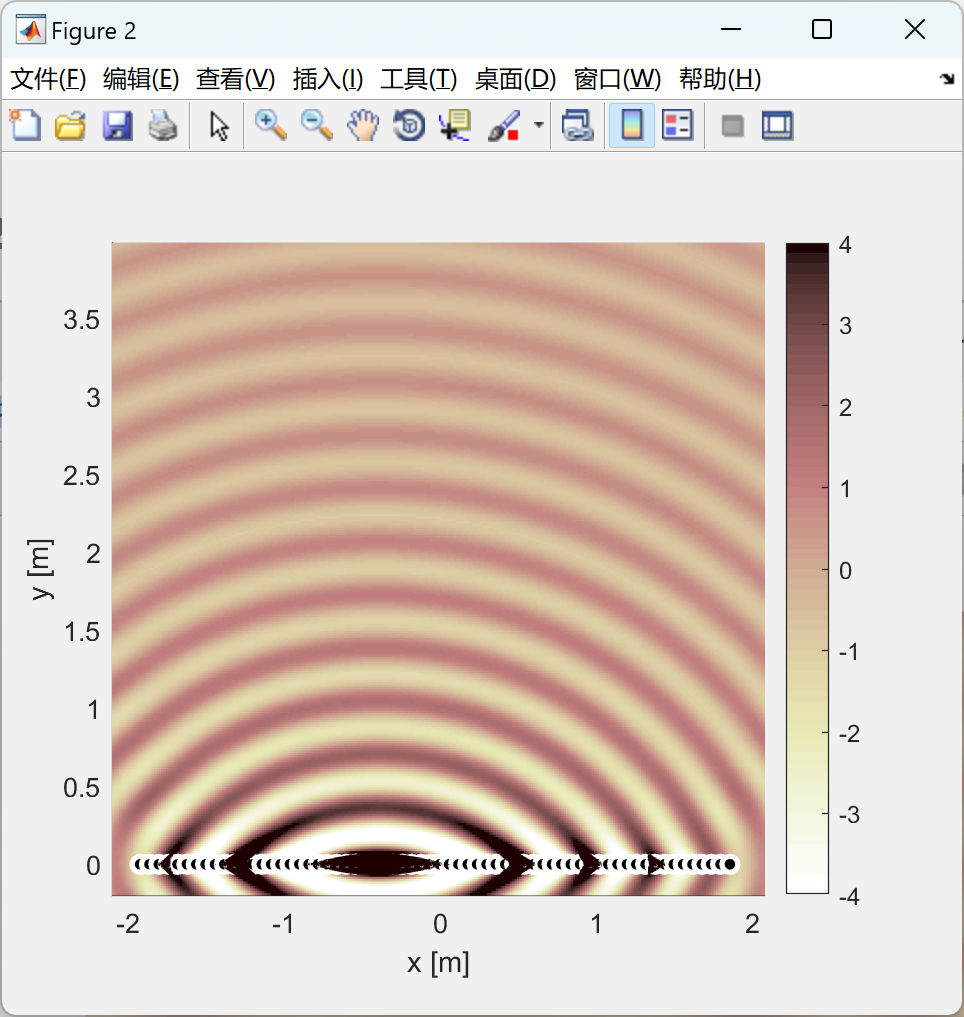
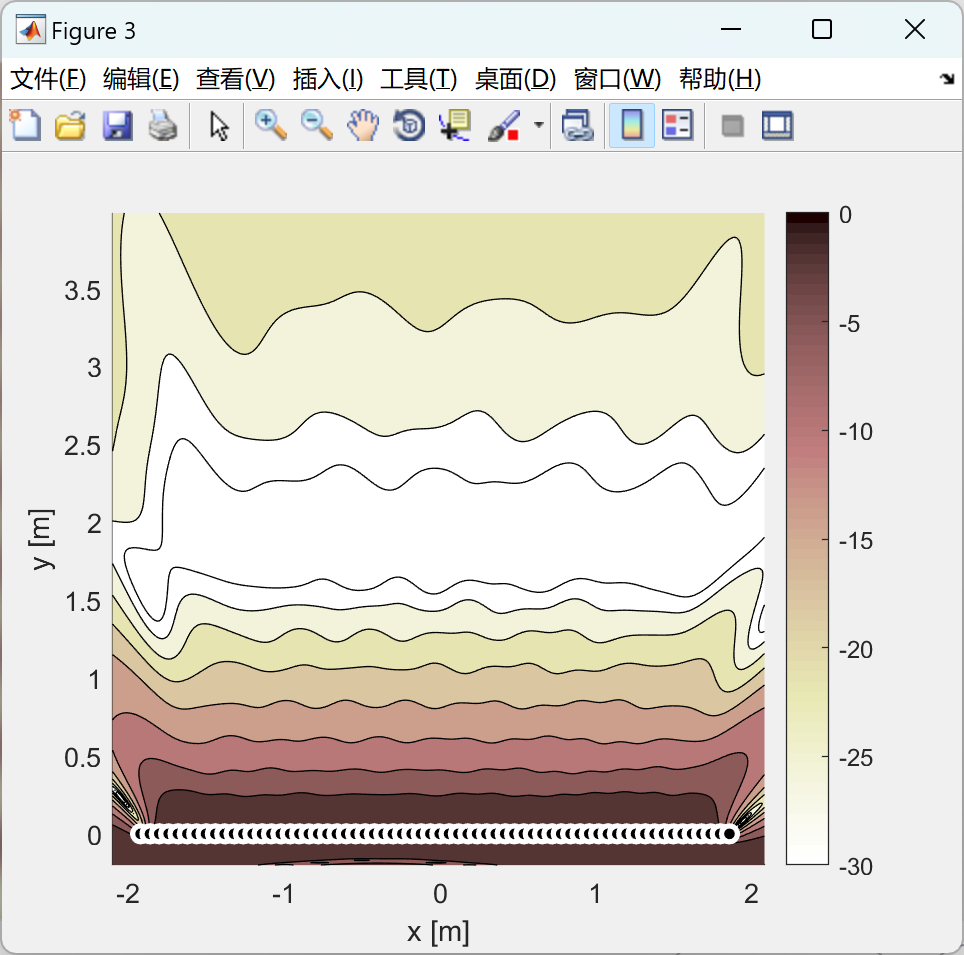
部分代码：

%% Parameters

WindowLocation;

%Sound velocity [m/s]
c=340.29;

%% Parameters: Reproduced area

%Size of reproduced area [m]
lenX=4.2;
lenY=4.2;

%Interval of reproduced area [m]
dx=0.015;
dy=0.015;

%Number of samples
Nx=round(lenX/dx);
Ny=round(lenY/dy);

%Positions
xr = (((0:Nx-1)-Nx/2).*dx)';
yr = ((0:Ny-1).*dy-0.2)';
zr = 0;

%% Parameters: Loudspeaker array

%Number of loudspeakers
Nsp = 64;

%Loudspeaker interval [m]
d_sp = 0.06;

%Array size [m]
len_sp = Nsp*d_sp;

%Positions
if mod(Nsp,2)==0
    x_sp = (((0:Nsp-1)-Nsp/2+0.005).*d_sp)';
else
    x_sp = (((0:Nsp-1)-(Nsp-1)/2).*d_sp)';
end
y_sp = zeros(Nsp,1);
z_sp = zeros(Nsp,1);

%% Parameters: Microphone array

%Number of microphones
Nm = Nsp;

%Microphone interval [m]
d_m = d_sp;

%Array size [m]
len_m = len_sp;

%Positions
x_m = x_sp;
y_m = y_sp;
z_m = z_sp;

%% Sound sources

%Number of sources
Nsrc = 1;

%Source type ('ps': point source, 'pw': plane wave)
src_type = 'ps';

%Source position [m]
xs = -0.4;
ys = -1.0;
zs = 0.0;

%Plane wave angle [rad]
theta_pw = 5/180*pi;

%Amplitude
amp = 10.0;

%Frequency
freq=1000;

%Wave number
k=2*pi*freq/c;

%% Spatial window function

win_sp=ones(Nsp,1);

taper_point=ceil(Nsp*0.10);
taper_vec=0.5-0.5.*cos(pi.*(1:taper_point)./taper_point);

win_sp(1:taper_point)=taper_vec;
win_sp(Nsp-taper_point+1:Nsp)=taper_vec(taper_point:-1:1);

%% Received signals of microphone array

sig = zeros(Nm,1);

%Point source
if strcmp(src_type,'ps')==1
    for iis=1:Nsrc
        H_s2m = green3d(x_m,y_m,z_m,xs(iis),ys(iis),zs(iis),k);
        sig = sig + amp(iis).*H_s2m;
    end
end
%Plane wave
if strcmp(src_type,'pw')==1
    for iis=1:Nsrc
        sig = sig + amp(iis).*exp(1i*(k*sin(theta_pw(iis))*x_m+k*cos(theta_pw(iis))*y_m));
    end
end

%% WFR filtering

%Spatial filter length
wfr_filter_len = 128;

%Spatial DFT length
Nf = 256;

%Reference line [m]
y_ref = 2.0;

%Shift [m]
shift.x = 0.0;
shift.y = 0.0;

%Spatial frequency
if mod(Nf,2)==0
    kx = (2*pi*([0:Nf/2-1, -Nf/2:-1]/Nf)/d_m)';
else
    kx = (2*pi*([0:(Nf-1)/2, -(Nf-1)/2:-1]/Nf)/d_m)';
end

%Spatial frequency window function
kx_c = k;
win_kx = (abs(kx)<kx_c);

%WFR filter
ky=sqrt(k^2-kx.^2);
Fwfr_spec=-4i.*exp(1i.*ky.*y_ref)./besselh(0,1,ky.*y_ref).*exp(-1i.*(kx.*shift.x+ky.*shift.y));

%Windowing in spatio-temporal frequency domain
Fwfr_spec = Fwfr_spec.*win_kx;

%Padding zero
Fwfr = fft(Fwfr_spec,Nf);

🎉3 参考文献

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。

Authors：Shoichi Koyama, Ken'ichi Furuya, Yusuke Hiwasaki & Yoichi Haneda

🌈4 Matlab代码及文章