【线性滤波逼近函数比较】结果显示每个滤波器的幅度、相位和群延迟、频率响应，并绘制了极点和零点图（Python代码实现）

 💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Python代码实现

---

💥1 概述

线性滤波逼近函数比较

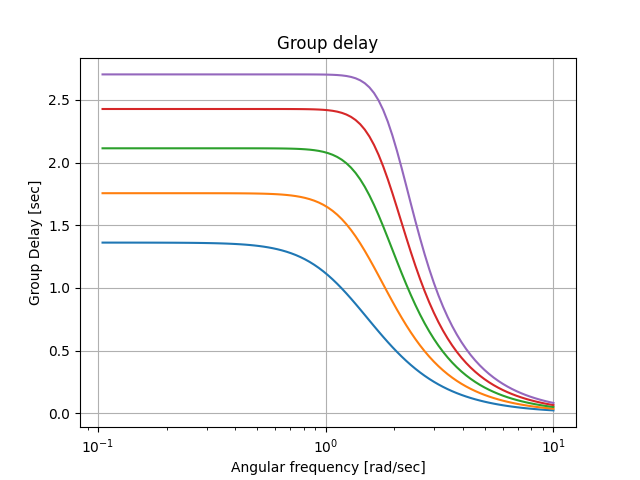
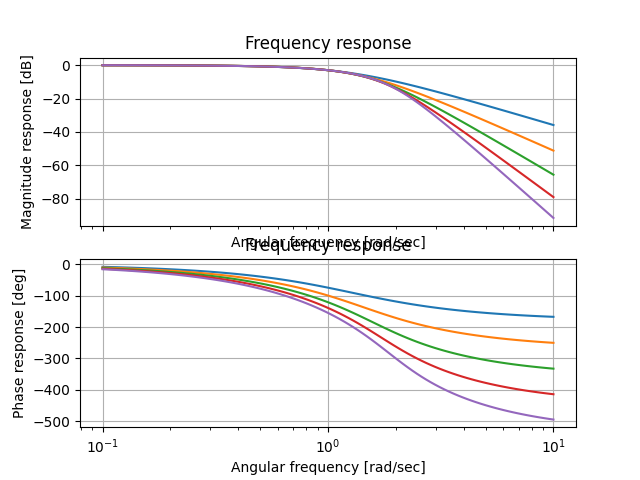
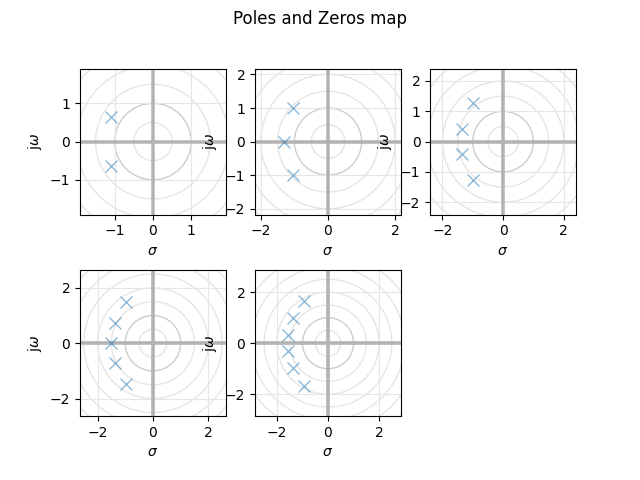
在本文中，比较了用于滤波应用的四种逼近函数（Butterworth、Chebyshev、Bessel和Cauer）的几个多项式阶数。结果显示了每个滤波器的幅度、相位和群延迟、频率响应，并绘制了极点和零点图。

本文旨在对滤波应用中常用的四种逼近函数（Butterworth、Chebyshev、Bessel和Cauer）进行多方面的比较和分析。通过对这些逼近函数在不同多项式阶数下的表现进行研究，我们得出了它们在滤波器设计中的优劣势。

在研究中，我们对每种滤波器的幅度、相位和群延迟、频率响应进行了详细的分析和比较。通过绘制出每个滤波器的极点和零点图，我们可以清晰地看到它们在频域中的特性和性能表现。

值得注意的是，我们不仅对每种逼近函数的理论性能进行了比较，还对它们在实际应用中的表现进行了验证。通过实际的滤波器设计和仿真实验，我们验证了研究结果的有效性和可靠性。

📚2 运行结果

部分代码：
 

## BODE plots
fig_hdl = 1
axes_hdl = ()

for ii in range(cant_sys):
    fig_hdl, axes_hdl = bodePlot(all_sys[ii], fig_hdl, axes_hdl)

plt.savefig('../results/bode.png')
plt.show()
## PZ Maps
fig_hdl = 2

pzmap(all_sys, fig_hdl)

plt.savefig('../results/pzmap.png')
plt.show()
## Group delay plots
fig_hdl = 3

for ii in range(cant_sys):
    fig_hdl = grpDelay(all_sys[ii], fig_hdl)

plt.savefig('../results/grpdelay.png')
plt.show()

🎉3 参考文献

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。

[1]闻建刚.非线性相位FIR滤波器的优化设计及应用[D].浙江工业大学,2019.

[2]马月超.高阶线性相位开关电容滤波器设计[D].哈尔滨工业大学[2024-01-18].DOI:CNKI:CDMD:2.1014.002659.

🌈4 Python代码实现