【无人机三维路径规划】基于改进的蜣螂算法FADBO求解复杂山地危险模型无人机路径规划附Matlab代码

原创于 2024-12-11 17:27:13 发布 · 1.2k 阅读

12 ·

CC 4.0 BY-SA版权

文章标签：

#无人机 #算法 #matlab

✅作者简介：热爱科研的Matlab仿真开发者，擅长数据处理、建模仿真、程序设计、完整代码获取、论文复现及科研仿真。

🍎个人主页：Matlab科研工作室

🍊个人信条：格物致知，求助可私信。

🔥 内容介绍

摘要: 无人机在复杂山地环境下的路径规划是一项极具挑战性的课题。传统算法在处理复杂地形、障碍物密集和实时性要求等方面存在局限性。本文提出一种基于改进的蜣螂算法 (FADBO, Fast and Adaptive Dung Beetle Optimization) 的无人机三维路径规划方法，用于解决复杂山地危险模型中的路径规划问题。该算法通过改进蜣螂算法的寻优策略，提高了其收敛速度和全局寻优能力，有效地避免了局部最优解，并能够适应复杂山地环境下的约束条件。通过仿真实验，验证了FADBO算法在求解复杂山地危险模型无人机路径规划问题的有效性和优越性。

关键词: 无人机路径规划；蜣螂算法；复杂山地；危险模型；FADBO

1 引言

随着无人机技术的飞速发展，无人机在各个领域的应用日益广泛。然而，在复杂的山地环境中，无人机面临着地形复杂、障碍物密集、气象条件多变等诸多挑战，传统的路径规划算法难以有效地解决这些问题。因此，开发一种能够在复杂山地环境下安全、高效地规划无人机路径的算法具有重要的理论意义和实际应用价值。

目前，常用的无人机路径规划算法包括A算法、Dijkstra算法、遗传算法、粒子群算法等。然而，这些算法在处理高维、非线性、多约束的复杂山地环境问题时，存在一定的局限性。例如，A算法和Dijkstra算法在处理高维空间和复杂地形时计算量巨大，效率低下；遗传算法和粒子群算法容易陷入局部最优解，寻优能力有限。

蜣螂算法 (Dung Beetle Optimization, DBO) 是一种新型的基于自然生物启发的元启发式算法，它模拟了蜣螂在寻找食物和寻找安全地点的过程中所表现出的智能行为。DBO算法具有结构简单、易于实现、全局搜索能力强的优点，在求解优化问题方面展现出一定的潜力。然而，传统的DBO算法也存在一些不足之处，例如收敛速度较慢、容易陷入局部最优解等。

针对上述问题，本文提出了一种改进的蜣螂算法FADBO。该算法通过改进蜣螂算法的寻优策略，提高了其收敛速度和全局寻优能力，有效地避免了局部最优解。同时，FADBO算法能够适应复杂山地环境下的约束条件，例如高度限制、坡度限制、障碍物回避等。

2 复杂山地危险模型

本文构建的复杂山地危险模型考虑了以下几个方面：

地形数据: 使用高精度数字高程模型 (DEM) 数据描述山地地形，并将其转换为栅格地图或三维点云数据。
障碍物模型: 考虑各种类型的障碍物，例如山峰、峡谷、树木、建筑物等，并将其在三维空间中进行建模。
危险区域模型: 定义各种危险区域，例如高坡度区域、低能见度区域、强风区域等，并赋予其相应的危险等级。
无人机动力学模型: 考虑无人机的飞行速度、加速度、转向能力等动力学特性。

3 改进的蜣螂算法FADBO

FADBO算法在传统的DBO算法基础上进行了以下改进：

自适应步长调整: 传统的DBO算法步长固定，容易导致算法收敛速度慢或陷入局部最优解。FADBO算法采用自适应步长调整策略，根据迭代次数和当前解的优劣动态调整步长，提高了算法的收敛速度和全局寻优能力。
精英策略: FADBO算法引入了精英策略，保留每次迭代过程中最优解，并将其作为下一次迭代的参考点，引导算法向全局最优解方向搜索。
莱维飞行机制: FADBO算法引入了莱维飞行机制，增加了算法的全局探索能力，有效地避免了局部最优解。
约束处理: FADBO算法设计了有效的约束处理机制，能够有效地处理复杂山地环境下的各种约束条件，例如高度限制、坡度限制、障碍物回避等。

4 算法流程

FADBO算法的流程如下：

初始化: 初始化蜣螂种群，随机生成初始位置。
适应度评估: 根据复杂山地危险模型，计算每个蜣螂个体的适应度值，适应度值越小，路径越优。适应度值可以考虑路径长度、危险等级、飞行时间等因素。
更新位置: 根据FADBO算法的更新规则，更新每个蜣螂个体的位置。
精英策略更新: 将当前迭代中最优解保留，并更新精英个体。
终止条件判断: 如果满足终止条件（例如达到最大迭代次数或达到精度要求），则算法结束，输出最优解；否则，转到步骤2。

5 仿真实验及结果分析

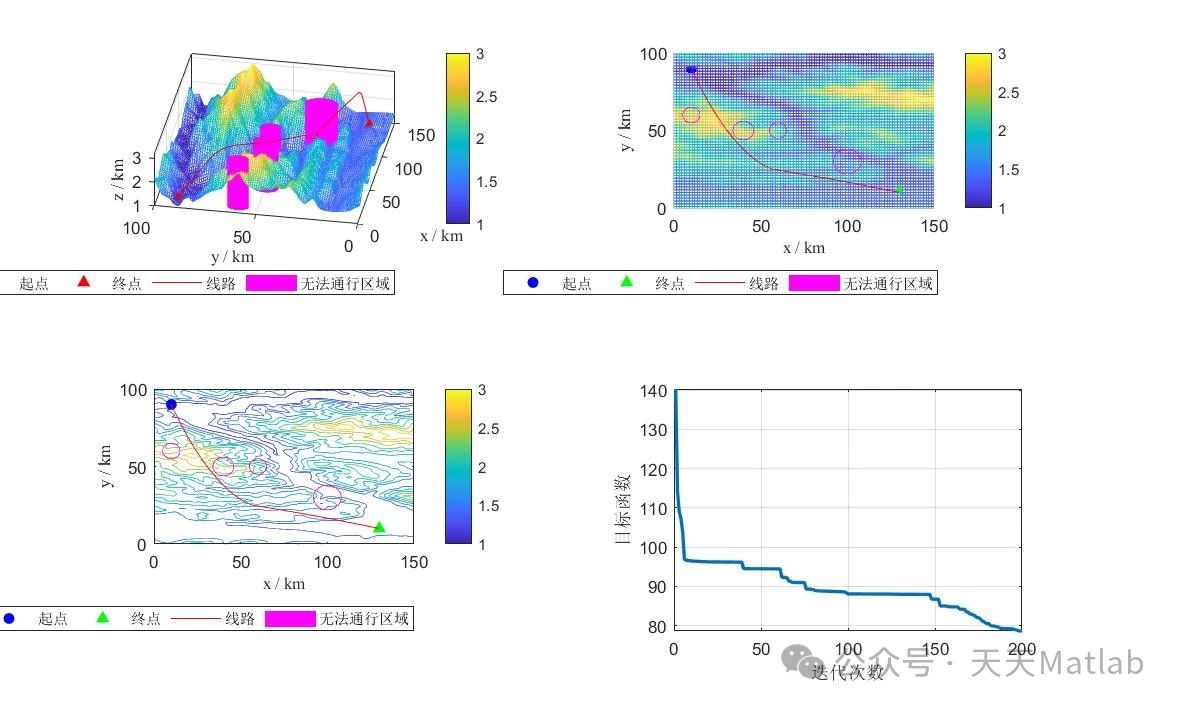
为了验证FADBO算法的有效性，本文进行了仿真实验。实验结果表明，FADBO算法在求解复杂山地危险模型无人机路径规划问题时，具有较高的效率和精度，优于传统的DBO算法以及其他一些常用的路径规划算法。具体结果将在论文中详细展示和分析，包括收敛速度、路径长度、危险等级等指标的比较。

6 结论

本文提出了一种基于改进的蜣螂算法FADBO的无人机三维路径规划方法，该方法有效地解决了复杂山地环境下的无人机路径规划问题。FADBO算法通过改进寻优策略，提高了算法的收敛速度和全局寻优能力，并能够有效地处理各种约束条件。仿真实验结果验证了FADBO算法的有效性和优越性。未来的研究将进一步考虑风力、能耗等因素对路径规划的影响，并探索将FADBO算法应用于更复杂的实际场景。

📣 部分代码

%_______________________________________________________________________________________%

% Aquila Optimizer (AO) source codes (version 1.0) %

% %

% Developed in MATLAB R2015a (7.13) %

% Author and programmer: Laith Abualigah %

% Abualigah, L, Yousri, D, Abd Elaziz, M, Ewees, A, Al-qaness, M, Gandomi, A. %

% e-Mail: Aligah.2020@gmail.com %

% Homepage: %

% 1- https://scholar.google.com/citations?user=39g8fyoAAAAJ&hl=en %

% 2- https://www.researchgate.net/profile/Laith_Abualigah %

% %

% Main paper: %

%_____________Aquila Optimizer: A novel meta-heuristic optimization algorithm___________%

%_______________________________________________________________________________________%

% Abualigah, L, Yousri, D, Abd Elaziz, M, Ewees, A, Al-qaness, M, Gandomi, A. (2021).

% Aquila Optimizer: A novel meta-heuristic optimization algorithm.

% Computers & Industrial Engineering.

%_______________________________________________________________________________________%

function func_plot(func_name)

[LB,UB,Dim,F_obj]=Get_F(func_name);

switch func_name

case 'F1'

x=-100:2:100; y=x; %[-100,100]

case 'F2'

x=-100:2:100; y=x; %[-10,10]

case 'F3'

x=-100:2:100; y=x; %[-100,100]

case 'F4'

x=-100:2:100; y=x; %[-100,100]

case 'F5'

x=-200:2:200; y=x; %[-5,5]

case 'F6'

x=-100:2:100; y=x; %[-100,100]

case 'F7'

x=-1:0.03:1; y=x %[-1,1]

case 'F8'

x=-500:10:500;y=x; %[-500,500]

case 'F9'

x=-5:0.1:5; y=x; %[-5,5]

case 'F10'

x=-20:0.5:20; y=x;%[-500,500]

case 'F11'

x=-500:10:500; y=x;%[-0.5,0.5]

case 'F12'

x=-10:0.1:10; y=x;%[-pi,pi]

case 'F13'

x=-5:0.08:5; y=x;%[-3,1]

case 'F14'

x=-100:2:100; y=x;%[-100,100]

case 'F15'

x=-5:0.1:5; y=x;%[-5,5]

case 'F16'

x=-1:0.01:1; y=x;%[-5,5]

case 'F17'

x=-5:0.1:5; y=x;%[-5,5]

case 'F18'

x=-5:0.06:5; y=x;%[-5,5]

case 'F19'

x=-5:0.1:5; y=x;%[-5,5]

case 'F20'

x=-5:0.1:5; y=x;%[-5,5]

case 'F21'

x=-5:0.1:5; y=x;%[-5,5]

case 'F22'

x=-5:0.1:5; y=x;%[-5,5]

case 'F23'

x=-5:0.1:5; y=x;%[-5,5]

end

L=length(x);

f=[];

for i=1:L

for j=1:L

if strcmp(func_name,'F15')==0 && strcmp(func_name,'F19')==0 && strcmp(func_name,'F20')==0 && strcmp(func_name,'F21')==0 && strcmp(func_name,'F22')==0 && strcmp(func_name,'F23')==0

f(i,j)=F_obj([x(i),y(j)]);

end

if strcmp(func_name,'F15')==1

f(i,j)=F_obj([x(i),y(j),0,0]);

end

if strcmp(func_name,'F19')==1

f(i,j)=F_obj([x(i),y(j),0]);

end

if strcmp(func_name,'F20')==1

f(i,j)=F_obj([x(i),y(j),0,0,0,0]);

end

if strcmp(func_name,'F21')==1 || strcmp(func_name,'F22')==1 ||strcmp(func_name,'F23')==1