最短路算法

已于 2024-03-06 09:50:53 修改
阅读量160 收藏
点赞数 1
文章标签： 算法
于 2023-04-03 19:58:03 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/Madtlg/article/details/129922910
版权
本文介绍了Dijkstra算法的原理、适用情况、步骤及伪代码实现，包括邻接表和邻接矩阵两种方法。接着讨论了Dijkstra算法无法处理负权边的原因，并展示了Bellman-Ford算法如何解决这一问题。此外，还介绍了SPFA算法的思路和过程，以及Floyd算法的初始化和应用。这些算法都是寻找图中节点间最短路径的关键工具。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

知识体系

朴素Dijkstra算法 

介绍：

Dijkstra算法是基于贪心的思想，每一步都找当前情况下的最优解，那么最后找出来的就是整体的最优解。

适用情况：

1.边权为正数

2.单源最短路

3.稠密图（n为点数，m为边数，n^2于m是一个级别，也就是边特别多）

图解步骤：

<1>用一个 dist 数组保存源点到其余各个节点的距离，dist[i] 表示源点到节点 i 的距离。初始时，dist 数组的各个元素为无穷大。
用一个状态数组 state 记录是否找到了源点到该节点的最短距离，state[i] 如果为真，则表示找到了源点到节点 i 的最短距离，state[i] 如果为假，则表示源点到节点 i 的最短距离还没有找到。初始时，state 各个元素为假。

<2>源点到源点的距离为 0。即dist[1] = 0。

<3>遍历 dist 数组，找到一个节点，这个节点是：没有确定最短路径的节点中距离源点最近的点。假设该节点编号为 i。此时就找到了源点到该节点的最短距离，state[i] 置为 1。

<4>遍历 i 所有可以到达的节点 j，如果 dist[j] 大于 dist[i] 加上 i -> j 的距离，即 dist[j] > dist[i] + w[i][j]（w[i][j] 为 i -> j 的距离） ，则更新 dist[j] = dist[i] + w[i][j]。

<5>重复 3 4 步骤，直到所有节点的状态都被置为 1。

<6>此时 dist 数组中，就保存了源点到其余各个节点的最短距离。

伪代码实现：

int dist[n],state[n];
dist[1] = 0, state[1] = 1;
for(i:1 ~ n)
{
    t <- 没有确定最短路径的节点中距离源点最近的点;
    state[t] = 1;
    更新 dist;
}

例题：

邻接表做法 ：

#include<iostream>
#include <cstring>
#include <algorithm>
using namespace std;

const int N = 510, M = 100010;

int h[N], e[M], ne[M], w[M], idx;//邻接表存储图
int state[N];//state 记录是否找到了源点到该节点的最短距离
int dist[N];//dist 数组保存源点到其余各个节点的距离
int n, m;//图的节点个数和边数

void add(int a, int b, int c)//插入边
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}

void Dijkstra()
{
    memset(dist, 0x3f, sizeof(dist));//dist 数组的各个元素为无穷大
    dist[1] = 0;//源点到源点的距离为置为 0
    for (int i = 0; i < n; i++)
    {
        int t = -1;
        for (int j = 1; j <= n; j++)//遍历 dist 数组，找到没有确定最短路径的节点中距离源点最近的点t
        {
            if (!state[j] && (t == -1 || dist[j] < dist[t]))
                t = j;
        }

        state[t] = 1;//state[i] 置为 1。

        for (int j = h[t]; j != -1; j = ne[j])//遍历 t 所有可以到达的节点 i
        {
            int i = e[j];
            dist[i] = min(dist[i], dist[t] + w[j]);//更新 dist[j]
        }


    }
}

int main()
{
    memset(h, -1, sizeof(h));//邻接表初始化

    cin >> n >> m;
    while (m--)//读入 m 条边
    {
        int a, b, w;
        cin >> a >> b >> w;
        add(a, b, w);
    }

    Dijkstra();
    if (dist[n] != 0x3f3f3f3f)//如果dist[n]被更新了，则存在路径
        cout << dist[n];
    else
        cout << "-1";
}

邻接矩阵做法：

#include<bits/stdc++.h>
using namespace std;

int dist[510];
int g[510][510];
int st[510];
int n,m;

int dijkstra()
{
    memset(dist,0x3f,sizeof(dist));
    dist[1]=0;
    
    for(int j=1;j<=n;j++)
    {
        int t=0;// dist[0]=0x3f3f3f3f
        for(int i=1;i<=n;i++)
        {
            if(st[i]==0&&dist[t]>dist[i])//找到1~n里没有确定的点中的最短路径点
            t=i;
        }
        st[t]=1;
        for(int i=1;i<=n;i++)
        dist[i]=min(dist[i],dist[t]+g[t][i]);
    }
    
    if(dist[n]==0x3f3f3f3f) return -1;  //如果第n个点路径为无穷大即不存在最低路径
    return dist[n];
}



int main()
{
    memset(g,0x3f,sizeof(g));
    
    cin>>n>>m;
    while(m--)
    {
        int a,b,z;
        cin>>a>>b>>z;
        g[a][b]=min(g[a][b],z);
    }
    
    cout<<dijkstra();
    return 0;
}

堆优化的Dijkstra

板子：

const int N = 2e5 + 10;
int key[N * 2], h[N * 2], ne[N * 2], idx, vue[N* 2], dist[N * 2], flag[N * 2];
void add(int u, int v, int x) {
	key[idx] = v;
	vue[idx] = x;
	ne[idx] = h[u];
	h[u] = idx++;
}

int dijkstra(int start, int n)//求start到n的最短路
{
    memset(dist, 0x3f, sizeof dist);//距离初始化为无穷大
    dist[start] = 0;
    std::priority_queue<std::pair<int, int>, std::vector<std::pair<int, int>>, std::greater<std::pair<int, int>>> heap;//小根堆
    heap.push({0, start});//插入距离和节点编号
 
    while (len(heap))
    {
        auto t = heap.top();//取距离源点最近的点
        heap.pop();
 
        int ver = t.second,distance = t.first;//ver:节点编号，distance:源点距离ver 的距离
 
        if (flag[ver]) continue;//如果距离已经确定，则跳过该点
        flag[ver] = 1;
 
        for (int i = h[ver]; i != -1; i = ne[i])//更新ver所指向的节点距离
        {
            int j = key[i];
            if (dist[j] > dist[ver] + vue[i])
            {
                dist[j] = distance+ vue[i];
                heap.push({dist[j], j});//距离变小，则入堆
            }
        }
    }
 
    if (dist[n] == 0x3f3f3f3f) return -1;
    return dist[n];
}

例题：

#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>//堆的头文件

using namespace std;

typedef pair<int, int> PII;//堆里存储距离和节点编号

const int N = 1e6 + 10;

int n, m;//节点数量和边数
int h[N], w[N], e[N], ne[N], idx;//邻接表存储图
int dist[N];//存储距离
bool st[N];//存储状态

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}

int dijkstra()
{
    memset(dist, 0x3f, sizeof dist);//距离初始化为无穷大
    dist[1] = 0;
    priority_queue<PII, vector<PII>, greater<PII>> heap;//小根堆
    heap.push({0, 1});//插入距离和节点编号

    while (heap.size())
    {
        auto t = heap.top();//取距离源点最近的点
        heap.pop();

        int ver = t.second,distance = t.first;//ver:节点编号，distance:源点距离ver 的距离

        if (st[ver]) continue;//如果距离已经确定，则跳过该点
        st[ver] = true;

        for (int i = h[ver]; i != -1; i = ne[i])//更新ver所指向的节点距离
        {
            int j = e[i];
            if (dist[j] > dist[ver] + w[i])
            {
                dist[j] = distance+ w[i];
                heap.push({dist[j], j});//距离变小，则入堆
            }
        }
    }

    if (dist[n] == 0x3f3f3f3f) return -1;
    return dist[n];
}

int main()
{
    scanf("%d%d", &n, &m);

    memset(h, -1, sizeof h);
    while (m -- )
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c);
    }

    cout << dijkstra() << endl;

    return 0;
}

 Bellman-frod

为什么Dijkstra不能解决含有负权边的问题？:

会发生串联

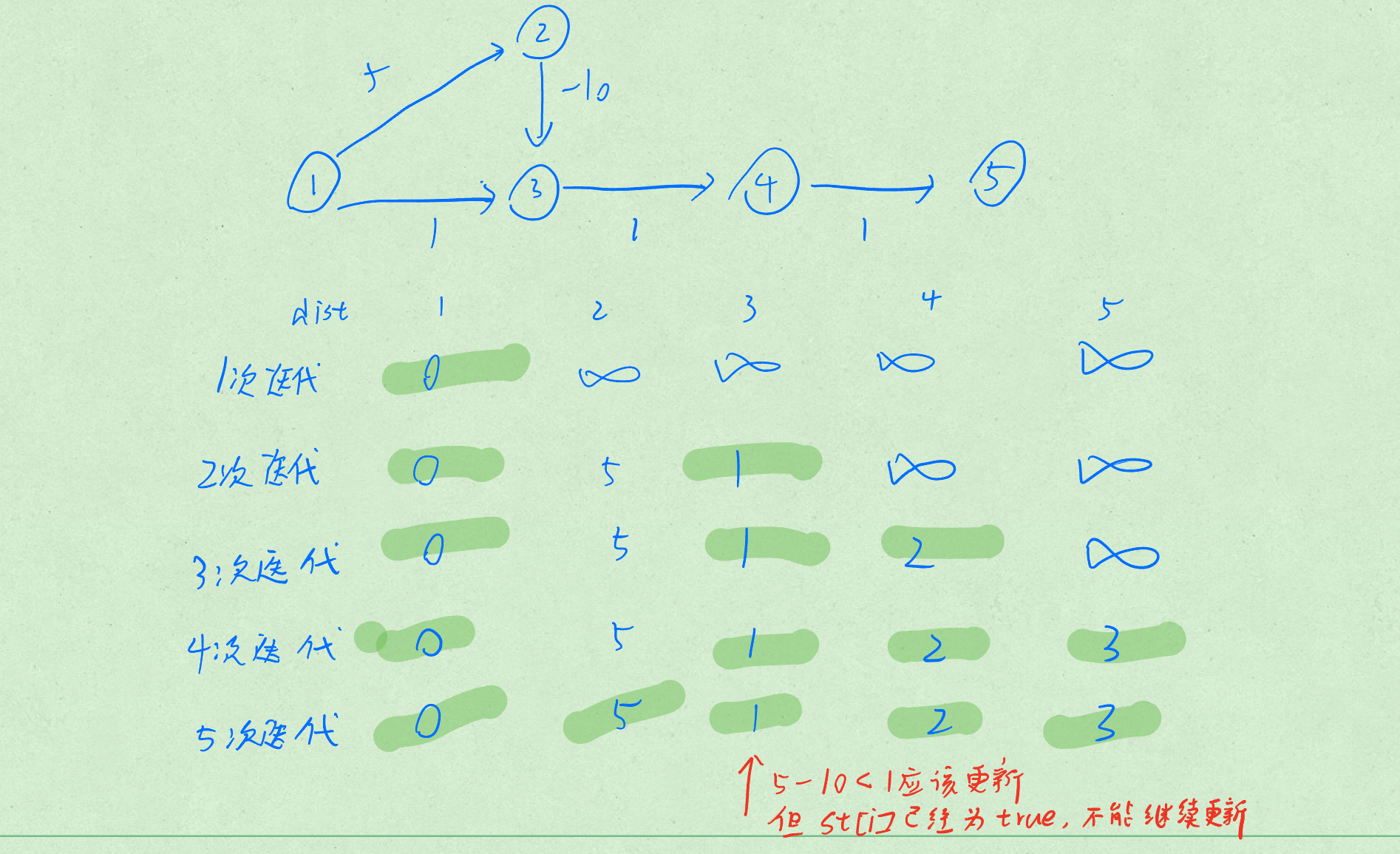
例题

#include <iostream>
#include <algorithm>
#include <cstring>


using namespace std;

const int N = 510,M = 10010;

struct Edge
{
    int a;//起点
    int b;//终点
    int w;//边的权重；
}e[M];
int dist[N];//存储当前点到起点的距离；
int back[N];//作为备份存储；
int n,m,k;//n个点，m条边，k为最大限制边数；

void bellman_ford()
{
    memset(dist ,0x3f, sizeof dist);//对距离数组初始化，所有边都为无穷大；
    dist[1] = 0;//起点到起点的距离为0;

    for(int i = 0;i < k;i++)//最大限制是k条边以内；
    {
        memcpy(back,dist,sizeof dist); //使用back 先将dist中的数据拷贝，防止出现串联更新；

        for(int j = 0;j < m; j++ )
        {
            int a = e[j].a;
            int b = e[j].b;
            int c = e[j].w;

            dist[b] = min(dist[b], back[a]+c);//每一条边都要比较更新，但是不会一直更新下去发生串联，而dijkstra算法则是一直会更新下去
        }
    }
}

int main()
{
    scanf("%d %d %d",&n,&m,&k);
    for(int i=0 ;i<m; i++)
    {
        int a,b,w;
        scanf("%d %d %d",&a,&b,&w);
        e[i] = {a,b,w};
    }
    bellman_ford(); 

    if(dist[n] > 0x3f3f3f/2) printf("impossible");
    else printf("%d",dist[n]);

    return 0;


}

spfa

求最短路：

思路过程：

1.建立一个队列，初始时队列里只有起始点。

2.再建立一个数组记录起始点到所有点的最短路径（该表格的初始值要赋为极大值，该点到他本身的路径赋为0）。

3.再建立一个数组，标记点是否在队列中。

4.队头不断出队，计算始点起点经过队头到其他点的距离是否变短，如果变短且被点不在队列中，则把该点加入到队尾。

5.重复执行直到队列为空。

6.在保存最短路径的数组中，就得到了最短路径

图解过程：

给定一个有向图，如下，求A~E的最短路。

源点A首先入队，然后A出队，计算出到BC的距离会变短，更新距离数组，BC没在队列中，BC入队

B出队，计算出到D的距离变短，更新距离数组，D没在队列中，D入队。然后C出队，无点可更新。

D出队，计算出到E的距离变短，更新距离数组，E没在队列中，E入队。

E出队，此时队列为空，源点到所有点的最短路已被找到，A->E的最短路即为8

例题

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;

const int N = 100010;
int h[N], e[N], w[N], ne[N], idx;//邻接表，存储图
int st[N];//标记顶点是不是在队列中
int dist[N];//保存最短路径的值
int q[N], hh, tt = -1;//队列

void add(int a, int b, int c){//图中添加边和边的端点
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}

void spfa(){
    q[++tt] = 1;//从1号顶点开始松弛，1号顶点入队
    dist[1] = 0;//1号到1号的距离为 0
    st[1] = 1;//1号顶点在队列中
    while(tt >= hh){//不断进行松弛
        int a = q[hh++];//取对头记作a，进行松弛
        st[a] = 0;//取完队头后，a不在队列中了
        for(int i = h[a]; i != -1; i = ne[i])//遍历所有和a相连的点
        {
            int b = e[i], c = w[i];//获得和a相连的点和边
            if(dist[b] > dist[a] + c){//如果可以距离变得更短，则更新距离

                dist[b] = dist[a] + c;//更新距离

                if(!st[b]){//如果没在队列中
                    q[++tt] = b;//入队
                    st[b] = 1;//打标记
                }
            }
        }
    }
}
int main(){
    memset(h, -1, sizeof h);//初始化邻接表
    memset(dist, 0x3f, sizeof dist);//初始化距离
    int n, m;//保存点的数量和边的数量
    cin >> n >> m;
    for(int i = 0; i < m; i++){//读入每条边和边的端点
        int a, b, w;
        cin >> a >> b >> w;
        add(a, b, w);//加入到邻接表
    }
    spfa();
    if(dist[n] == 0x3f3f3f3f )//如果到n点的距离是无穷，则不能到达 
        cout << "impossible";
    else cout << dist[n];//否则能到达，输出距离
    return 0;
}

练习：E-小红勇闯地下城_牛客周赛 Round 33 (nowcoder.com)

Floyd

初始化：
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= n; j ++ )
            if (i == j) d[i][j] = 0;
            else d[i][j] = INF;

// 算法结束后，d[a][b]表示a到b的最短距离
void floyd()
{
    for (int k = 1; k <= n; k ++ )
        for (int i = 1; i <= n; i ++ )
            for (int j = 1; j <= n; j ++ )
                d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}

独陷泥沼
关注
8.3.2 蓝桥杯图论之Johnson全源最短路
tang7mj的博客
01-31 496
Johnson算法结合了Bellman-Ford算法和Dijkstra算法的优点，能够在带有负权边的图中计算全源最短路径。其核心思想是先使用Bellman-Ford算法重新赋权，以消除负权边的影响，然后对每个顶点运行Dijkstra算法计算最短路径。Johnson算法通过巧妙地结合Bellman-Ford算法和Dijkstra算法，提供了一种在包含负权边的图中计算全源最短路径的有效方法。通过本文的介绍，您应该能够理解Johnson算法的原理和步骤，并知道如何在C++中实现它。
【论题选编】稠密图最短路
zqy1018的blog
08-21 424
有的最短路题目中，可能边的数目很大，朴素建图边的数目为 O(∣V∣2)O(|V|^2)O(∣V∣2)。这样很难直接应用 Dijkstra 算法等。 对付这种图，一般采用的策略是： 去除无用选项。有可能两点之间直接连接的路径长一定不是最短路径，这样就可以排除大多数路径，只构造那些有用的边。 构造等价选项。有可能两点之间的路径长完全等价于按照某种简单模式形成的路径长，这样就可以考虑这种简单的模式。 优化建图方式。例如建立虚拟点，以代替完全子图中各个点之间的相互连边。 例 1：最短路 1 题意：有 nnn 个
最短路问题（四种算法与路径还原算法）
ltrbless的博客
10-05 2167
1、Bellman-Ford算法： 用Bellman-Ford算法求解单源最短路径问题，单源最短路径是指固定一个起点，求它到其他所有点的最短路问题。 struct edge { int from, to, cost; //从顶点from指向顶点to的权值为cost的边 }; edge es[MAX_E]; //边 int d[MAX_V]; //到出发点的最短距离 int ...
最短路问题
m0_73612605的博客
03-10 1061
只介绍模板不介绍原理一.单源最短路（从一个点到其他所有点的最短距离）1.所有边权都是正数1）朴素Dijkstra算法 O（n^2） 稠密图//n为节点数，m为边数2）堆优化版Dijkstra算法 O（mlogn）稀疏图2.存在负权边（有负权回路时最短路可能不存在）1）Bellman-Ford O（nm）//擅长解决有边数限制的2）SPFA 一般：O（m） 最坏：O（nm）//Bellman-Ford的优化二.多源汇最短路（任意一点到所有点的最短距离）
Johnson全源最短路
Z7784562的博客
09-03 337
Johnson全源最短路 思路： 对于NNN个顶点MMM条边的图怎么求全源最短路？ Floyd，时间复杂度O(N3)O(N^3)O(N3)。 NNN次Bellman-Ford/SPFA,以每个顶点为源点跑一遍，时间复杂度O(N2M)O(N^2M)O(N2M),在稠密图中比Floyd还慢，即使尝试一些如SLF的玄学优化也会被特定数据卡掉。 NNN次Dijkstra，时间复杂度O(NMlog⁡M)O(NM\log M)O(NMlogM),弊端是无法处理负边权。 那么是不是可以考虑把所有边权变非负？ 考虑如果
最短路算法详解
qq_59539549的博客
06-25 2786
图的最短路算法
图论-最短路算法
weixin_57140993的博客
05-16 890
初始化邻接矩阵（有边直接连接的直接存，没有的存INF最大值，自己到自己的路径长度为0）遍历（k，i，j）更新i到j的最短路，通过k依据题意更新答案。
【算法】最短路算法
白晨的博客
02-25 3725
这次为大家分享的是图论中的最短路算法。考虑到最短路算法的复杂性以及本文新手向的教程，本次算法讲解列举了大量例子并且配上了大量动图。篇文章所有的代码实现都是算法向的，以快速实现和效率为主，如果出现算法向的代码实在看不懂，可以参考白晨的工程向实现的代码
最短路算法及其在物流管理中的应用 (2013年)
06-14
最短路算法是图论中的重要算法之一，广泛应用于网络优化、地图导航、交通规划等领域。在物流管理中，最短路算法能够帮助解决配送路径问题和配送中心选址问题，是物流系统规划的重要支持工具。 首先，Dijkstra算法是...
算法合集之《最短路算法及其应用》
02-26
最短路算法是图论中的一个核心问题，广泛应用于计算机科学、运筹学、网络优化等领域。本资源《最短路算法及其应用》主要探讨了如何寻找网络中两点间最短路径的方法，以及这些方法在实际问题中的应用，如交通路线规划...
基于Python实现的最短路算法水流动画设计源码
10-02
本项目是一个详细的Python实现的最短路算法水流动画设计源码，其内容丰富，包含了117个文件，分为多个类型，具有高度的专业性和研究价值。项目中包含的104个PNG图像文件，可以看作是算法过程的静态展示，每一个图像...
动态最短路_动态最短路算法程序_
10-03
动态最短路算法是图论中的一个重要概念，用于在带权重的有向或无向图中寻找从一个起点到其他所有节点的最短路径。在实际应用中，它广泛应用于网络设计、物流优化、交通路线规划等领域。在这个场景中，我们讨论的是...
蓝桥杯 19.合根植物
wuqingshun314159的博客
04-22 428
如果我们告诉你哪些小格子之间出现了合根现象，你能计算出这个园中一共有多少株合根植物吗？输出一个整数，表示最后园中合根植物的数量。每个格子里种了一株合根植物。，从而与另一个格子的植物合成为一体。这种植物有个特点，它的根可能会沿着。这个是非常简单纯粹的并查集题目。W 星球的一个种植园被分成。
LeetCode算法题(Go语言实现)_54
LuckyLay的博客
04-21 628
方法优势适用场景二分查找时间效率高静态数据查询线性扫描无需预处理小规模数据哈希预处理快速查询频繁重复查询。
【力扣刷题实战】找到字符串中所有字母异位词
knowledge_Cheese的博客
04-22 1093
这里的emplace_back 函数 是 std::vector 容器提供的成员函数。它的作用是在 vector 的尾部直接构造新元素，而不是像 push_back 那样先创建一个临时对象，再将其拷贝或移动到 vector 尾部。的 ASCII 值映射到 0 到 25 的索引范围，所以使用长度为 26 的向量来存储每个字母的计数。的异位词的起始索引。异位词指的是由相同字母重排列形成的字符串（包括相同的字符串）。中字符的频率，找出所有异位词的起始位置。如果相等，说明字符串。的函数，它的主要功能是在字符串。
算法之动态规划
qq_68194402的博客
04-21 1367
动态规划（Dynamic Programming, DP）是一种解决复杂问题的算法设计技术，适用于具有“重叠子问题”和“最优子结构”性质的问题。动态规划将问题分解成更小的子问题，通过解决这些子问题来解决原始问题。这种方法的关键在于避免重复计算。一旦解决了一个子问题，它的解就被存储起来，以便后续需要时直接使用，从而避免了重复计算。这种记忆化的技术称为“缓存”。
代码随想录算法训练营第60期第十七天打卡
最新发布
2401_83782806的博客
04-25 564
今天的题目还是挺有意思的，我们也接触了二叉搜索树，最大二叉树是一道不错的题目，我们学会了递归与分割数组，合并二叉树其实还是递归，随后的两道题我们接触了二叉搜索树，大家自己要去消化一下，我们明天再见！
[贪心_7] 最优除法 | 跳跃游戏 II | 加油站
一个人知道自己为什么而活，他就能够接收任何一种生活
04-25 656
对步数 实现双指针 区间的维护模拟，来看 要走多少步 利用单调性：i=i+step 发现有一个起点点都跑不到某个位置，那中间的都不用在考虑了，不用在枚举了。
最短路算法详解与应用
"最短路算法的PPT讲义，主要涵盖了如何详细描述和总结最短路算法。" 最短路算法是图论中的一个重要概念，用于寻找图中两个节点之间的最短路径。常见的最短路算法有Dijkstra算法、Floyd-Warshall算法和Bellman-Ford...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值