插入排序与希尔排序

1. 插入排序 O（n^2）

1. 思路：

把n个待排序的元素看成一个有序表和一个无序表，开始时有序表中只包含1个元素，

无序表中包含n-1个元素，排序过程中每次从无序表中取出第1个元素，将它插入到

有序表中的适合位置，使之成为新的有序表，重复n-1次可完成。

2. 图解过程：

以5、2、4、6、1、3为例。（升序）

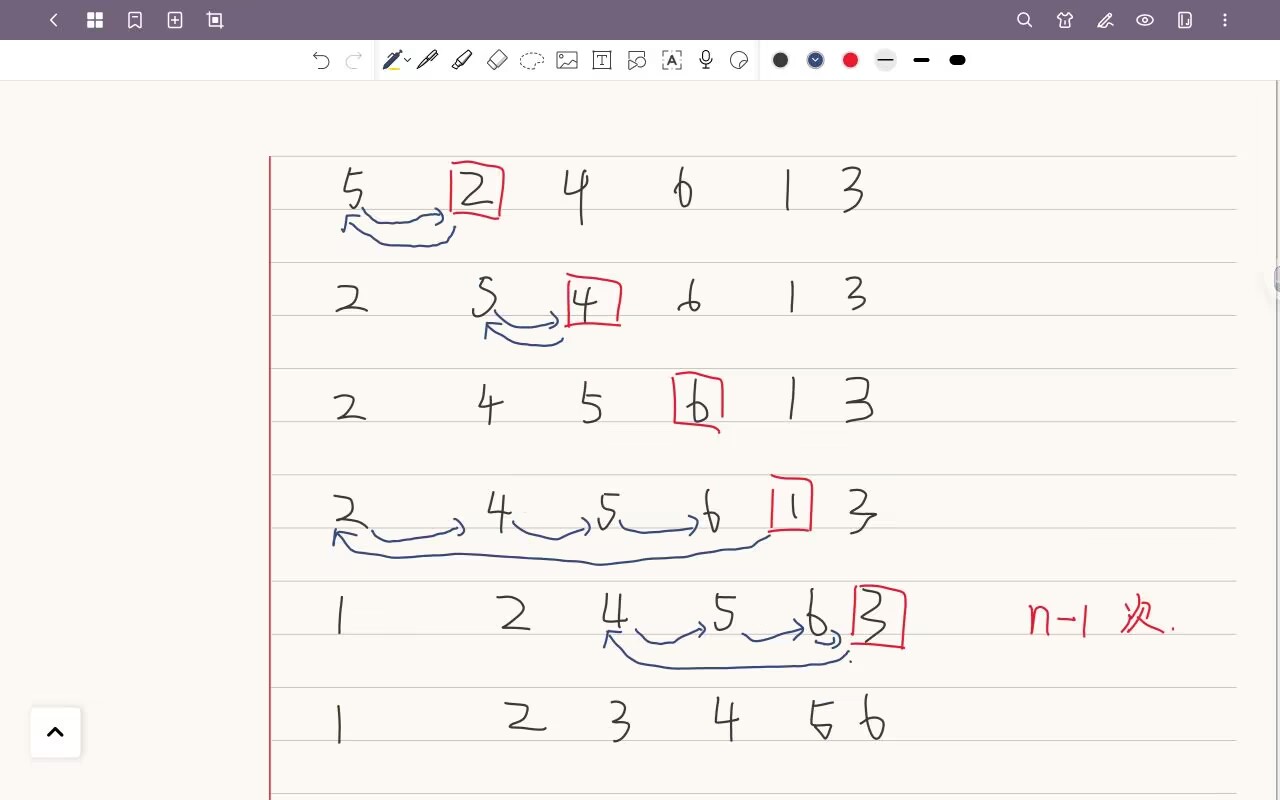
3. 代码实现：

将待排序数据保存在arr数组中。

for(int i=1;i<n;i++) //外层循环控制轮数，n-1轮
{
    for(int j=i;j>0;j--) //数组从下标为0开始保存数据
    {
        if(arr[j]<arr[j-1]) //如果当前位置比前一位置的数据小，就交换
        {
            swap(arr[j],arr[j-1]);
        }
        else break; //否则就说明 该数 已到达有序表的合适位置
    }               //（前面已经是有序表，前一个数比该数小,那么前面的所有数都比该数小）
}

2. 希尔排序 O(n-log n)-O(n^2)

1. 思路：

把记录按照下标的一定增量（gap）分组，对每组使用插入排序算法。随着增量逐渐减少，

每组包含的元素越来越多，当增量减至1时，整个数组被分为一组算法便终止。

2.图解过程：

以29、38、65、87、78、23、27、72、55、48为例

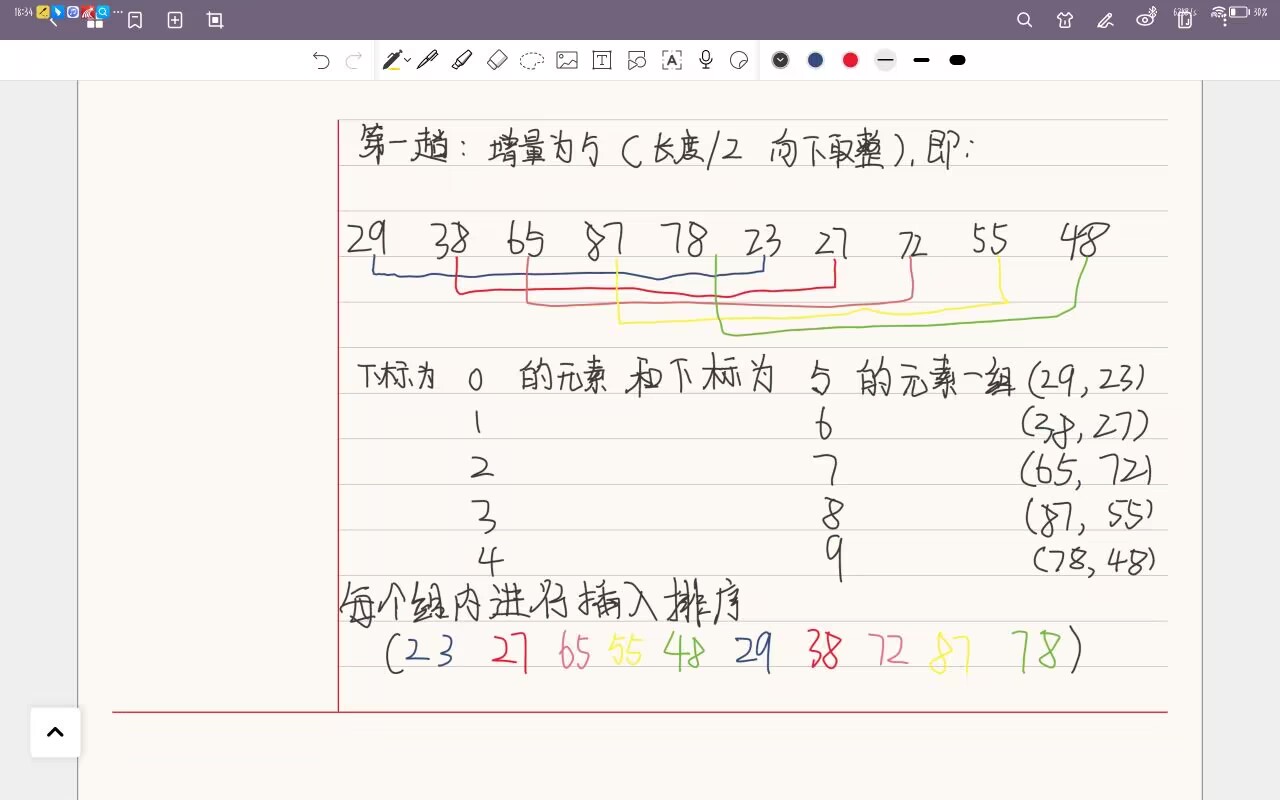
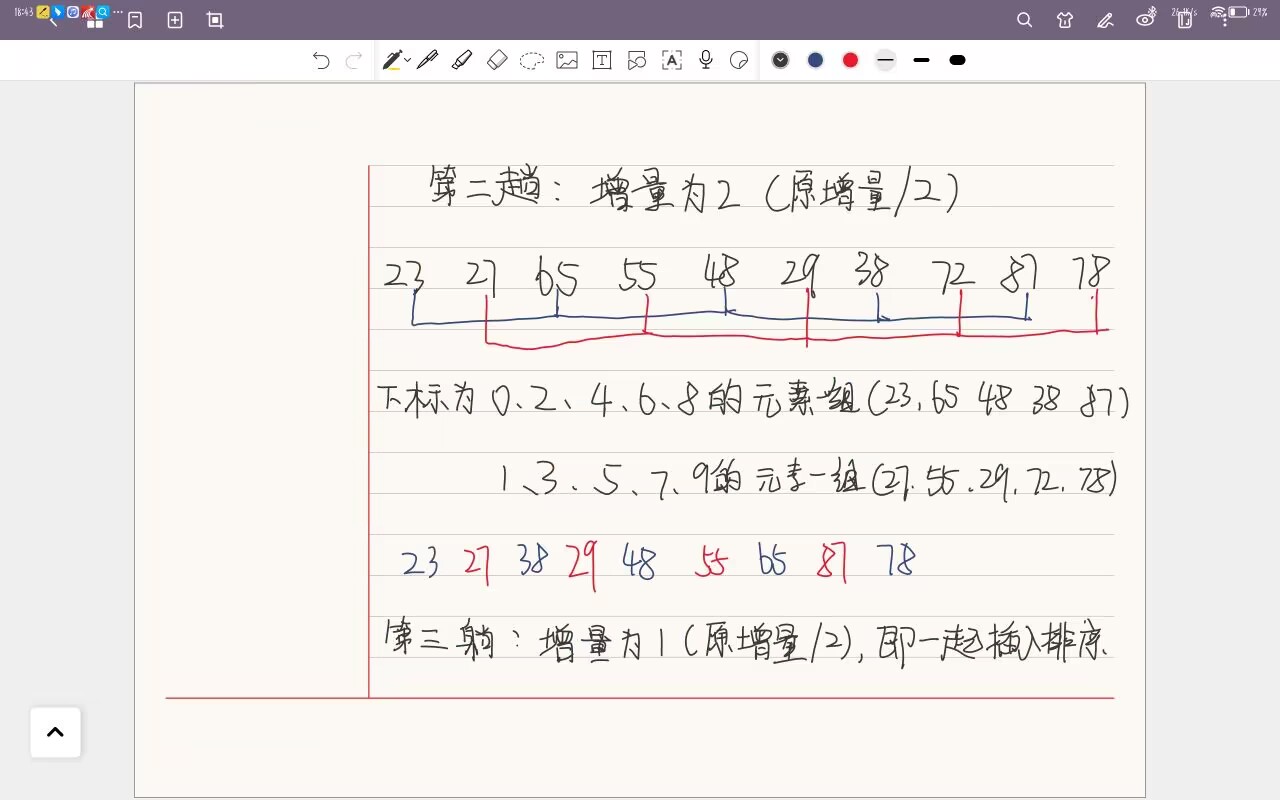
3.代码实现：

for(int gap=n/2;gap>0;gap/=2)
{
    for(int i=gap;i<n;i++)
    {
        for(int j=i;j>=gap;j-=gap)//同组比较，组内交换，注意边界
        {
            if(arr[j]<arr[j-gap])
            {
                swap(arr[j],arr[j-gap]);
            }
            else break;
        }
    }
}