并查集详解-优快云博客

本文链接：https://blog.youkuaiyun.com/Madtlg/article/details/129821600

并查集是一种用于处理不相交集合合并和查询的数据结构。文章详细介绍了其基本构成，包括find()函数（路径压缩优化）和join()函数（加权标记法优化）。初始化和合并策略是通过路径压缩提高效率，而加权标记法则通过比较节点的秩（高度）来优化合并过程，以空间换取时间。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

定义：

一种树型数据结构，用于处理不相交集合的合并，及查询问题。

构成：

pre[] //记录上一节点是谁

find(x) //查找 x 属于哪个集合（返回该集合的根节点）

join(x,y) //合并 x y 所在的集合

find()的实现

int find(x)
{
    while(pre[x]!=x) x=pre[x];
    return x;
}

find()改进——路径压缩

int find(x)
{
    if(pre[x]!=x) pre[x]=find(pre[x]);
    return x;
}

注：路径压缩的find有个小缺陷，只有当查找到某个结点代表元（根节点）后，才能对该查找路径

上的各节点进行路径压缩。也就是说，压缩效果在该次查询操作生效之后才会生效。

join()实现

void join(int x,int y)
{
    if(find(x)!=find(y)) p[find(x)]=find(y);
}

join()改进——加权标记法（按秩合并）

核心思想：空间换时间

思路：将树中所有节点增设一个权值 rank，用以表示该节点所在树的高度

注：只进行根节点权值的比较

图解:

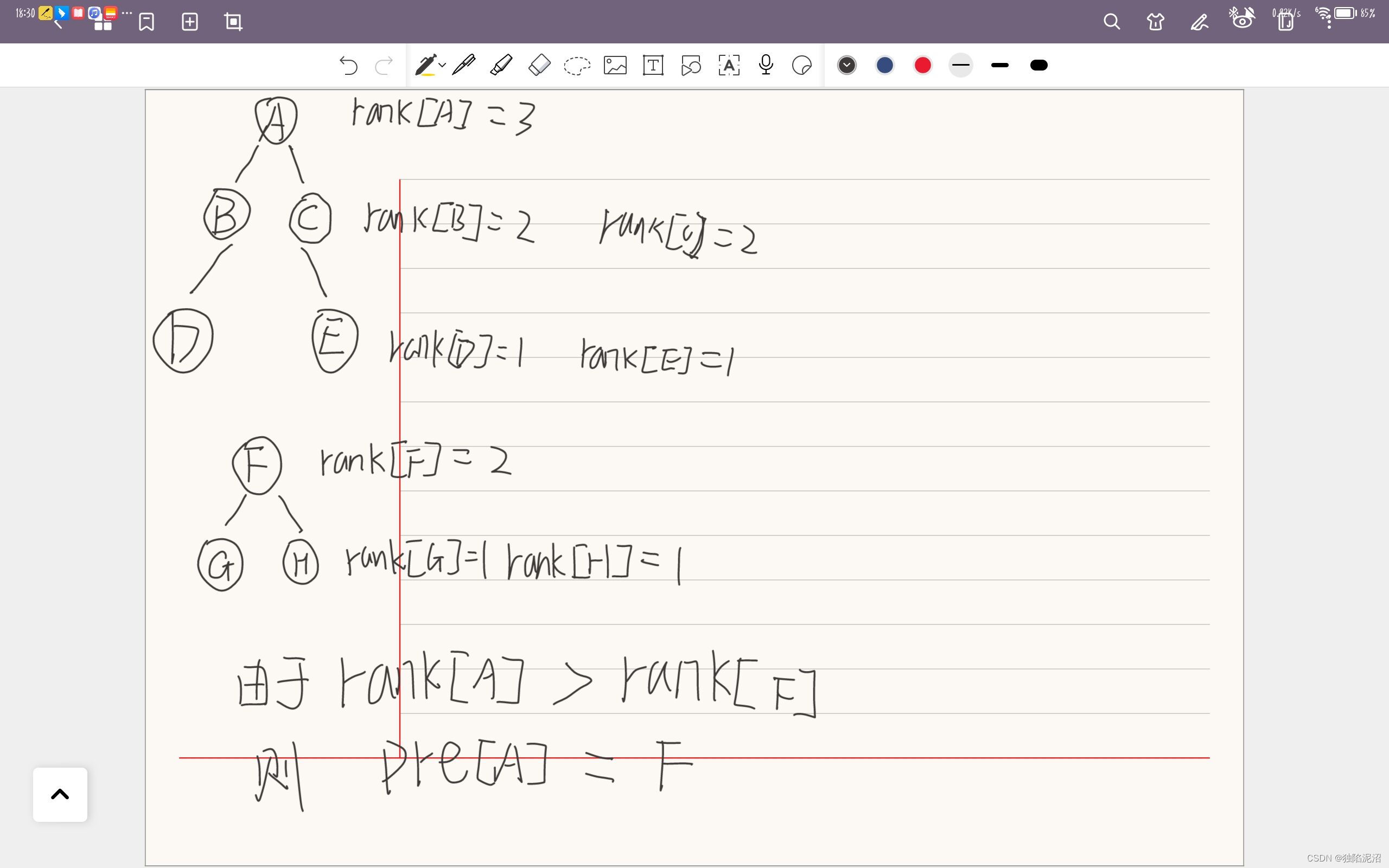
//初始化
void init(int n)
{
    for(int i=0;i<n;i++)
    {
        pre[i]=i;//使每个节点的上级都是自己
        rank[i]=1;//每个节点构成的树的高度为 1
    }
}

//join的加权优化
bool join(int x,int y)
{
    x=find(x),y=find(y);
    
    if(x==y) return false;//共属一个集合，无需合并
    
    if(rank[x] > rank[y]) pre[y] = x;//如果x的高度大于y，则使y的上一节点为x
    
    else
    {
        if(rank[x] == rank[y]) rank[y]++;
        pre[x] = y;
    }
    //如果x的高度和y相等，则令y的高度加1，使x的上一节点为y
    return true;
}