python-leetcode-111. 二叉树的最小深度

111. 二叉树的最小深度 - 力扣（LeetCode）

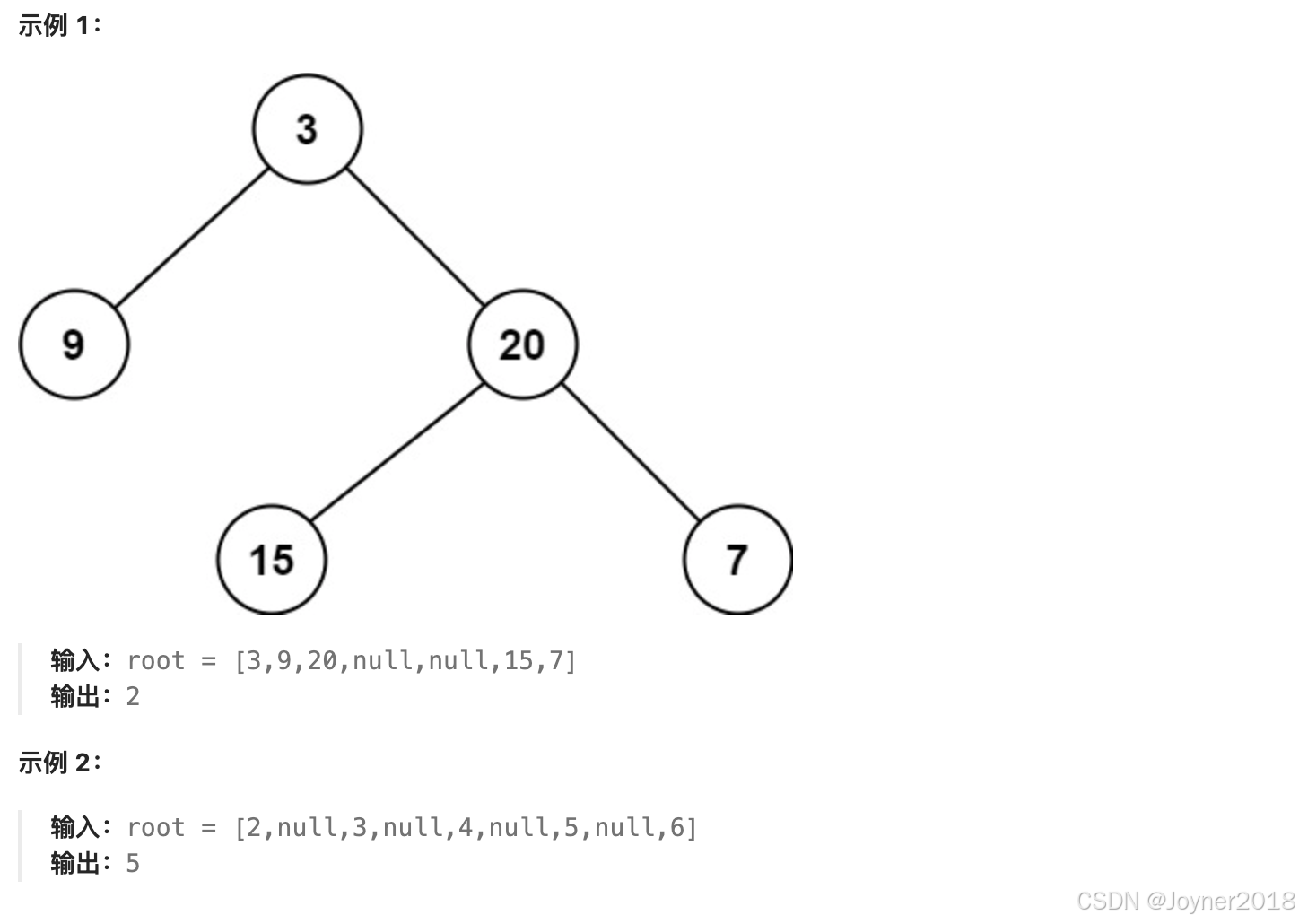
可以使用递归或迭代的方法来求解二叉树的最小深度。以下是递归解法和 BFS（广度优先搜索）解法：

递归解法

如果根节点为空，则最小深度为 0。如果左子树或右子树为空，则返回非空子树的深度，否则返回左右子树深度的较小值加 1。

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

def minDepth(root):
    if not root:
        return 0
    if not root.left:
        return minDepth(root.right) + 1
    if not root.right:
        return minDepth(root.left) + 1
    return min(minDepth(root.left), minDepth(root.right)) + 1

BFS 解法（推荐）

使用队列进行层序遍历，遇到第一个叶子节点时返回当前深度。

from collections import deque

def minDepth(root):
    if not root:
        return 0
    queue = deque([(root, 1)])  # (节点, 深度)
    while queue:
        node, depth = queue.popleft()
        if not node.left and not node.right:  # 叶子节点
            return depth
        if node.left:
            queue.append((node.left, depth + 1))
        if node.right:
            queue.append((node.right, depth + 1))

复杂度分析

• 递归解法: 最坏情况下（单链表形式），时间复杂度为 O(N)。
• BFS 解法: 最好情况下（叶子节点靠近根），时间复杂度为 O(log⁡N)，最坏情况下 O(N)，但在实际应用中更快。

BFS 适用于大规模数据集，因为它在找到第一个叶子节点后立即返回，而 DFS 可能会遍历整个树。