python-leetcode-119. 杨辉三角 II

119. 杨辉三角 II - 力扣（LeetCode）

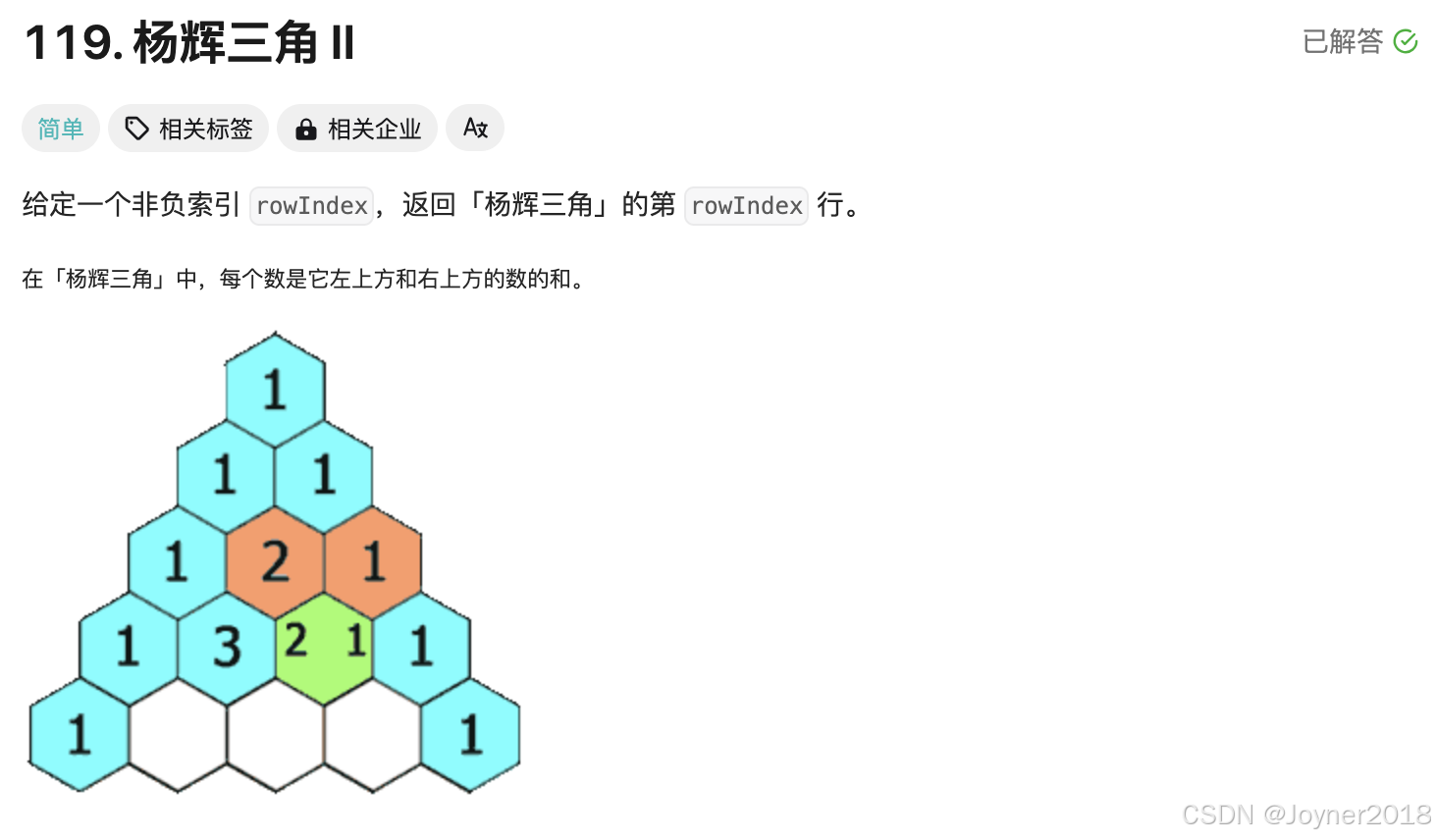
可以使用动态规划的方法来计算「杨辉三角」的第 rowIndex 行。我们可以从前往后构造这一行，而不需要存储整个三角形。这里是 Python 代码：

def getRow(rowIndex):
    row = [1] * (rowIndex + 1)
    for i in range(2, rowIndex + 1):
        for j in range(i - 1, 0, -1):
            row[j] += row[j - 1]
    return row

# 测试
print(getRow(3))  # 输出 [1, 3, 3, 1]

解释：

1. 初始化 row 数组，全为 1，长度为 rowIndex + 1。
2. 使用双层循环：
   • i 从 2 开始遍历到 rowIndex。
   • j 逆序遍历从 i-1 到 1，更新 row[j] = row[j] + row[j-1]。
3. 逆序更新可以避免覆盖未更新的值，保证计算正确。

这样，我们可以在 O(rowIndex^2) 时间复杂度和 O(rowIndex) 额外空间复杂度下计算杨辉三角的某一行。