粒子群算法求解物流配送路线问题（python）

粒子群算法求解物流配送路线问题（python）

1.查找论文文献

找一篇物流配送路径优化+粒子群算法求解的论文

参考文献：基于混沌粒子群算法的物流配送路径优化

2.了解粒子群算法的原理

讲解通俗易懂，有数学实例的博文：https://blog.youkuaiyun.com/daaikuaichuan/article/details/81382794
可参考文献：车辆路径问题的粒子群算法研究
里面给出了粒子群算法求解一般VRP问题的算法实现步骤。

3.确定编码方式和解码策略

3.1编码方式

物流配送路线的粒子编码方式：

3.2解码策略

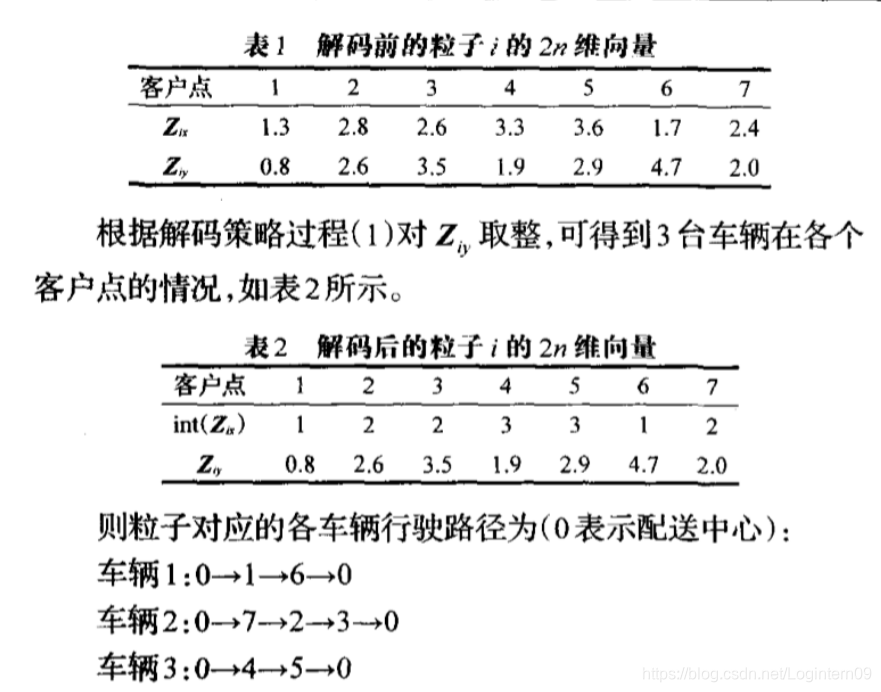
例如 ， 假如一个有 7个客户点， 3台车辆的物流配送问题 ，
其第 i 个粒子的位置向量 z如表 1所示

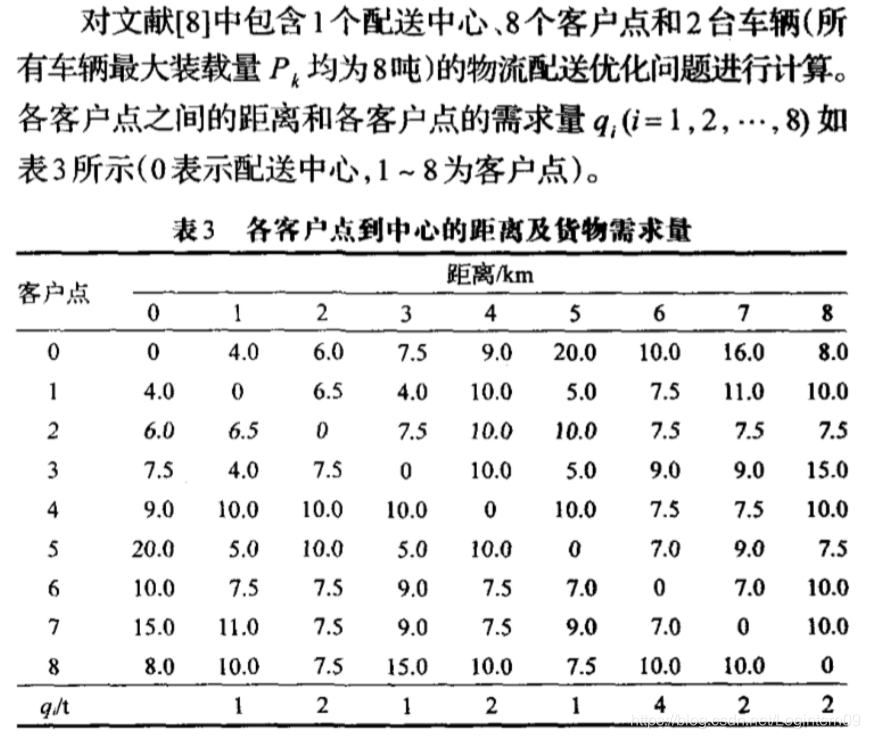
4.算例的输入参数

5.处理关键技术

5.1将不可行解转化为可行解

在迭代过程中形成的粒子可能是不满足数学模型约束条件的不可行解，要将进化生成的不可行解转变为可行解。

def get_feasible_x(x):
    # 修正粒子为满足约束的可行解粒子，超过其范围时按边界取值
    vehicle_element = np.rint(x[:demand_node_num])  # 取整数表示哪辆车拜访哪个客户点
    for index in range(len(vehicle_element)):
    	# x_bound = [[1, vehicle_num], [1, demand_node_num]]  # 自变量的上下限限制
        if vehicle_element[index] < x_bound[0][0]:
            vehicle_element[index] = x_bound[0][0]
        elif vehicle_element[index] > x_bound[0][1]:
            vehicle_element[index] = x_bound[0][1]
    x[:demand_node_num] = vehicle_element
    return x

判断生成的粒子是否满足车辆最大行驶里程数限制和车辆最大装载量约束限制，若不满足上述的两个条件的其一，则随机生成新的粒子直到满足所有的约束条件。
文献：车辆路径问题的粒子群算法研究
采用的方式是：对于有某条路径上的各发货任务的总需求量超过此条路径配送车容量的不可行解，则将该方案的评价值置为一个可行解不可达到的极大值。

def get_feasible_solution(x):
    """
    # 判断是否满足车辆最大行驶里程数限制和车辆最大载重量限制，若原粒子不满足条件则生成满足约束条件的可行解
    :param x: x为一个粒子
    :return:
    """
    x = get_feasible_x(x)
    length, total_path_list = calculate_fitness(x)
    result_list = []
    for i in range(len(total_path_list)):
        path_list = total_path_list[i]
        path_length = 0
        for j in range(len(path_list)-1):
            segment = [path_list[j], path_list[j+1]]
            path_length += distance_graph[segment[0], segment[1]]
        if path_length > length_max:
            new_x = set_codeForm(1)[0]
            result_list.append(False)
        else:
            # 候选解满足车辆行驶最大里程数要求，再判断车辆的实际装载量是否在最大装载量范围内
            path_list = total_path_list[i][1:-1]
            capacity = sum([quantity_graph[j-1] for j in path_list])
            if capacity > capacity_max:
                new_x = set_codeForm(1)[0]
                result_list.append(False)
            else:
                result_list.append(True)
    if False not in result_list:
        return x, length, total_path_list
    else:
        return get_feasible_solution(new_x)

5.2根据解码规则计算适应度函数值

优化物流配送路径问题的粒子群编码方式类似于遗传算法的双层整数编码方式，第一层片段上面的数字表示客户点由哪辆车来进行配送，该表示方法的最大优点是使每个客户需求点都得到车辆的配送服务，并限制每个需求点的需求仅能由某一车辆来完成 ，使解的可行化过程计算大大减少；第二层利用数字的大小来确定车辆拜访各个由它服务的客户点的次序。
该算例的适应度函数值为车辆的总行驶里程数最小。

def calculate_fitness(x):
    """
    # 计算适应度函数
    :param x: x为一个粒子
    :return:
    """
    # x = [[1.6,1.3,2.9,2.5,3.4,3.5,1.3,2,3,1,2,2,1,1]]
    total_path_list = []
    vehicle_element = x[:demand_node_num]
    path_element = x[demand_node_num:]
    actual_vehicle = list(set(vehicle_element))
    for j in range(len(actual_vehicle)):
        # customer_list表示第j辆车负责配送的客户位置索引列表
        customer_list = np.where(vehicle_element == actual_vehicle[j])
        path_list = path_element[customer_list]
        path_list = [customer_list[0][customer_index] for customer_index in np.argsort(path_list)]
        path_list = [element + 1 for element in path_list]
        path_list.insert(0, 0)
        path_list.append(0)
        # path_list表示第j辆车访问各个客户节点的拜访顺序
        total_path_list.append(path_list)
    # 0-3-1-2-0
    total_length = 0
    for path in total_path_list:
        for index in range(len(path)-1):
            segment = [path[index], path[index+1]]
            total_length += distance_graph[segment[0]][segment[1]]
    return total_length, total_path_list

6.算例结果

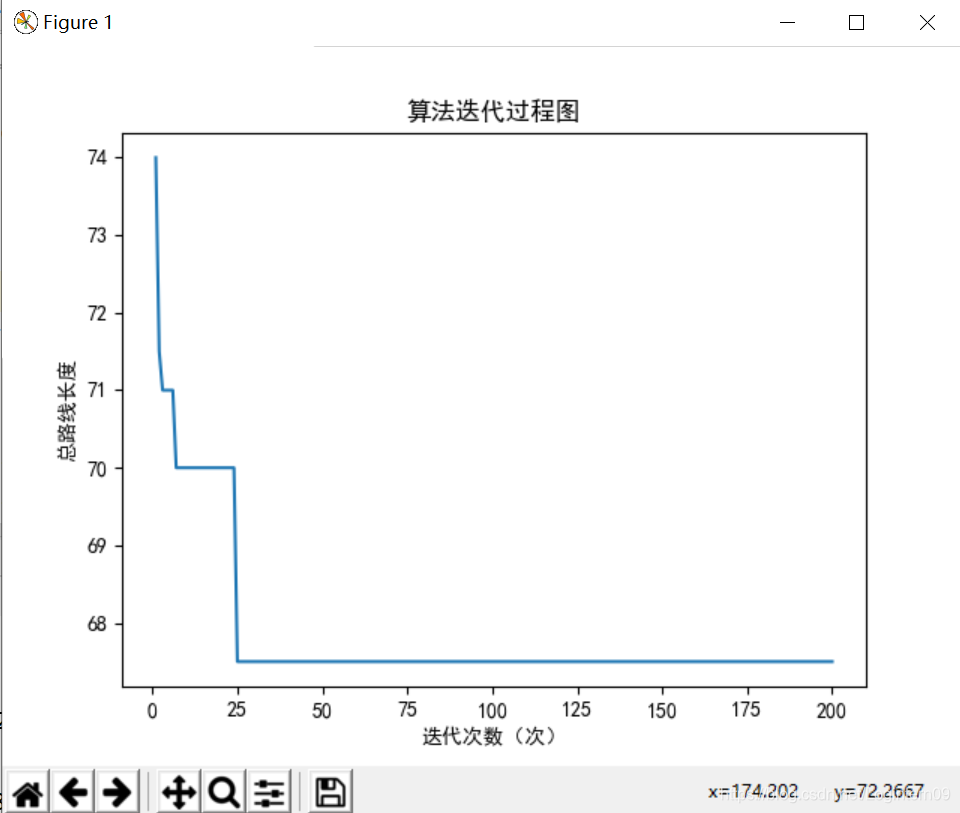
运行python3程序，运行环境为win64，pycharm2019.3.2，在某一次运行中得到的算例结果如下：

全局最优解结构为： [1. 1. 1. 2. 1. 2. 2. 1. 4. 7. 6. 6. 6. 4. 4. 6.]
最优路线长度为： 67.5
最优车辆运行路线为： [[0, 1, 3, 5, 8, 2, 0], [0, 6, 7, 4, 0]]，表示车辆1的配送方案为：0-1-3-5-8-2-0（从配送中心0出发依次访问客户点1、客户点3、客户点5、客户点8和客户点2，最后再返回配送中心）；车辆2的配送方案为：0-6-7-4-0。

参考文献：
Matlab实现粒子群算法的程序代码：https://www.cnblogs.com/kexinxin/p/9858664.html
matlab代码求解函数最优值：https://blog.youkuaiyun.com/zyqblog/article/details/80829043

numpy模块中矩阵和数组的区别：https://www.cnblogs.com/wj-1314/p/10244807.html
random模块的常用方法：https://www.cnblogs.com/liangmingshen/p/8909376.html
numpy模块入门级用法介绍：
https://www.jianshu.com/p/3e566f09a0cf
matplotlib模块简单使用技巧：https://www.cnblogs.com/bainianminguo/p/10952586.html
PYTHON 画图神器 Matplotlib：https://www.jianshu.com/p/c41ac57cea33