Python-Numpy的使用2023.10.14

Numpy——一个在Python中做科学计算的基础库，重在数值计算，也是大部分Python科学计算库的基础库，多用于在大型、多维数组上执行数值运算

import numpy as np

一.创建ndarray数组        

        NumPy最重要的一个特点就是其N维数组对象（即ndarray），该对象是一个快速而灵活的大数据集容器。你可以这种数组对整块数据执行一些数学运算，其语法跟标量元素之间的运算一样。

创建nadaary数组函数：

import numpy as np;

print ('使用列表生成一维数组')
data = [1,2,3,4,5,6]
x = np.array(data)
print (x) #打印数组
print(x.dtype)  # 打印数组元素的类型

print('使用列表生成二维数组')
data = [[1,2],[3,4],[5,6]]
x = np.array(data)
print(x)  # 打印数组
print(x.ndim)  # 打印数组的维度
print(x.shape)  # 打印数组各个维度的长度。shape是一个元组

print('使用zero/ones/empty创建数组:根据shape来创建')
x = np.zeros(6) #创建一维长度为6的，元素都是0一维数组
print(x)
x = np.zeros((2,3)) #创建一维长度为2，二维长度为3的二维0数组
print(x)
x = np.ones((2,3)) #创建一维长度为2，二维长度为3的二维1数组
print(x)
x = np.empty((3,3)) #创建一维长度为2，二维长度为3,未初始化的二维数组
print(x)

print('使用arrange生成连续元素')
print(np.arange(6))  # [0,1,2,3,4,5,] 开区间
print(np.arange(0, 6, 2))  # [0, 2，4]

二.指定ndarray数组元素的类型

        1.Numpy数据类型

numpy的数值类型实际上是dtype对象的实例，并对应唯一的字符，包括np.bool，np.int32，np.float32等等

import numpy as np;

print('生成指定元素类型的数组:设置dtype属性')
x = np.array([1,2.6,3],dtype = np.int64)
print(x)  # 元素类型为int64
print(x.dtype)
x = np.array([1,2,3],dtype = np.float64)
print(x)  # 元素类型为float64
print(x.dtype)

print('使用astype复制数组，并转换类型')
x = np.array([1,2.6,3],dtype = np.float64)
y = x.astype(np.int32)
print(y)  # [1 2 3]
print(x)  # [ 1.   2.6  3. ]
z = y.astype(np.float64)
print(z)  # [ 1.  2.  3.]

print('将字符串元素转换为数值元素')
x = np.array(['1','2','3'],dtype = np.string_)
y = x.astype(np.int32)
print(x)  # ['1' '2' '3']
print(y)  # [1 2 3] 若转换失败会抛出异常

print('使用其他数组的数据类型作为参数')
x = np.array([ 1., 2.6,3. ],dtype = np.float32);
y = np.arange(3,dtype=np.int32);
print(y)  # [0 1 2]
print(y.astype(x.dtype))  # [ 0.  1.  2.]

三.ndarray运算：

        1.元素级运算

a = np.array([1,2,3,4])
b = np.arange(4)
print(a, b)   # [1 2 3 4] [0 1 2 3]
print(a - b)  # [1 1 1 1]
print(a * b)  #[ 0  2  6 12]
print(a ** 2) #[ 1  4  9 16]
print(2 * np.sin(a))  #[ 1.68294197  1.81859485  0.28224002 -1.51360499]
print(a > 2)  #[False False  True  True]
print(np.exp(a))  # (指数)[ 2.71828183  7.3890561  20.08553692 54.59815003]

        2.矩阵运算

import numpy as np

a = np.array([[1,2],[3,4]]) # 2行2列
b = np.arange(6).reshape((2,3)) #2行3列
print(a.dot(b)) #矩阵相乘，2行3列

四.ndarray数组的基本索引和切片

• arr[r1:r2, c1:c2]
• arr[1,1] 等价 arr[1][1]
• [:] 代表某个维度的数据

在print('ndarray的基本索引')
x = np.array([[1, 2], [3, 4], [5, 6]])
print(x[0])  # [1,2]
print(x[0][1])  # 2,普通python数组的索引
print(x[0, 1])  # 同x[0][1]，ndarray数组的索引
x = np.array([[[1, 2], [3, 4]], [[5, 6], [7, 8]]])
print(x[0])  # [[1 2],[3 4]]
y = x[0].copy()  # 生成一个副本
z = x[0]  # 未生成一个副本
print(y)  # [[1 2],[3 4]]
print(y[0, 0])  # 1
y[0, 0] = 0
z[0, 0] = -1
print(y)  # [[0 2],[3 4]]
print(x[0])  # [[-1 2],[3 4]]
print(z)  # [[-1 2],[3 4]]

print('ndarray的切片')
x = np.array([1, 2, 3, 4, 5])
print(x[1:3])  # [2,3] 右边开区间
print(x[:3])  # [1,2,3] 左边默认为 0
print(x[1:])  # [2,3,4,5] 右边默认为元素个数
print(x[0:4:2])  # [1,3] 下标递增2
x = np.array([[1, 2], [3, 4], [5, 6]])
print(x[:2])  # [[1 2],[3 4]]
print(x[:2, :1])  # [[1],[3]]
x[:2, :1] = 0  # 用标量赋值
print(x)  # [[0,2],[0,4],[5,6]]
x[:2, :1] = [[8], [6]]  # 用数组赋值
print(x)  # [[8,2],[6,4],[5,6]]

五.ndarray数组的布尔索引和花式索引

布尔索引：使用布尔数组作为索引。arr[condition]，condition为一个条件/多个条件组成的布尔数组

print('ndarray的布尔型索引')
x = np.array([3, 2, 3, 1, 3, 0])
# 布尔型数组的长度必须跟被索引的轴长度一致
y = np.array([True, False, True, False, True, False])
print(x[y])  # [3,3,3]
print(x[y == False])  # [2,1,0]
print(x >= 3)  # [ True False  True False  True  False]
print(x[~(x >= 3)])  # [2,1,0]
print((x == 2) | (x == 1))  # [False  True False  True False False]
print(x[(x == 2) | (x == 1)])  # [2 1]
x[(x == 2) | (x == 1)] = 0
print(x)  # [3 0 3 0 3 0]

花式索引：以整形数组作为索引

print('ndarray的花式索引:使用整型数组作为索引')
x = np.array([1, 2, 3, 4, 5, 6])
print(x[[0, 1, 2]])  # [1 2 3]
print(x[[-1, -2, -3]])  # [6,5,4]
x = np.array([[1, 2], [3, 4], [5, 6]])
print(x[[0, 1]])  # [[1,2],[3,4]]
print(x[[0, 1], [0, 1]])  # [1,4] 打印x[0][0]和x[1][1]
print(x[[0, 1]][:, [0, 1]])  # 打印01行的01列 [[1,2],[3,4]]
# 使用np.ix_()函数增强可读性
print(x[np.ix_([0, 1], [0, 1])])  # 同上 打印01行的01列 [[1,2],[3,4]]
x[[0, 1], [0, 1]] = [0, 0]
print(x)  # [[0,2],[3,0],[5,6]]

六.ndarray数组的转置和轴对换

数组的转置/轴对换只会返回原数据的一个视图，不会改变原数据

print('ndarray数组的转置和轴对换')
k = np.arange(9)  # [0,1,....8]
m = k.reshape((3, 3))  # 改变数组的shape复制生成2维的，每个维度长度为3的数组
print(k)  # [0 1 2 3 4 5 6 7 8]
print(m)  # [[0 1 2] [3 4 5] [6 7 8]]
# 转置(矩阵)数组：T属性 : mT[x][y] = m[y][x]
print(m.T)  # [[0 3 6] [1 4 7] [2 5 8]]
# 计算矩阵的内积 xTx
print(np.dot(m, m.T))  # np.dot点乘
# 高维数组的轴对象
k = np.arange(8).reshape(2, 2, 2)
print(k)  # [[[0 1],[2 3]],[[4 5],[6 7]]]
print(k[1][0][0])
# 轴变换 transpose 参数:由轴编号组成的元组
m = k.transpose((1, 0, 2))  # m[y][x][z] = k[x][y][z]
print(m)  # [[[0 1],[4 5]],[[2 3],[6 7]]]
print(m[0][1][0])
# 轴交换 swapaxes (axes：轴)，参数:一对轴编号
m = k.swapaxes(0, 1)  # 将第一个轴和第二个轴交换 m[y][x][z] = k[x][y][z]
print(m)  # [[[0 1],[4 5]],[[2 3],[6 7]]]
print(m[0][1][0])
# 使用轴交换进行数组矩阵转置
m = np.arange(9).reshape((3, 3))
print(m)  # [[0 1 2] [3 4 5] [6 7 8]]
print(m.swapaxes(1, 0))  # [[0 3 6] [1 4 7] [2 5 8]]

七.ndarray通用函数

1.一元ufunc

print('一元ufunc示例')
x = np.arange(6)
print(x)  # [0 1 2 3 4 5]
print(np.square(x))  # [ 0  1  4  9 16 25]
x = np.array([1.5, 1.6, 1.7, 1.8])
y, z = np.modf(x)  #将数组的小数和整数部分以两个独立数组的形式返回
print(y)  # [ 0.5  0.6  0.7  0.8]
print(z)  # [ 1.  1.  1.  1.]

2.二元ufunc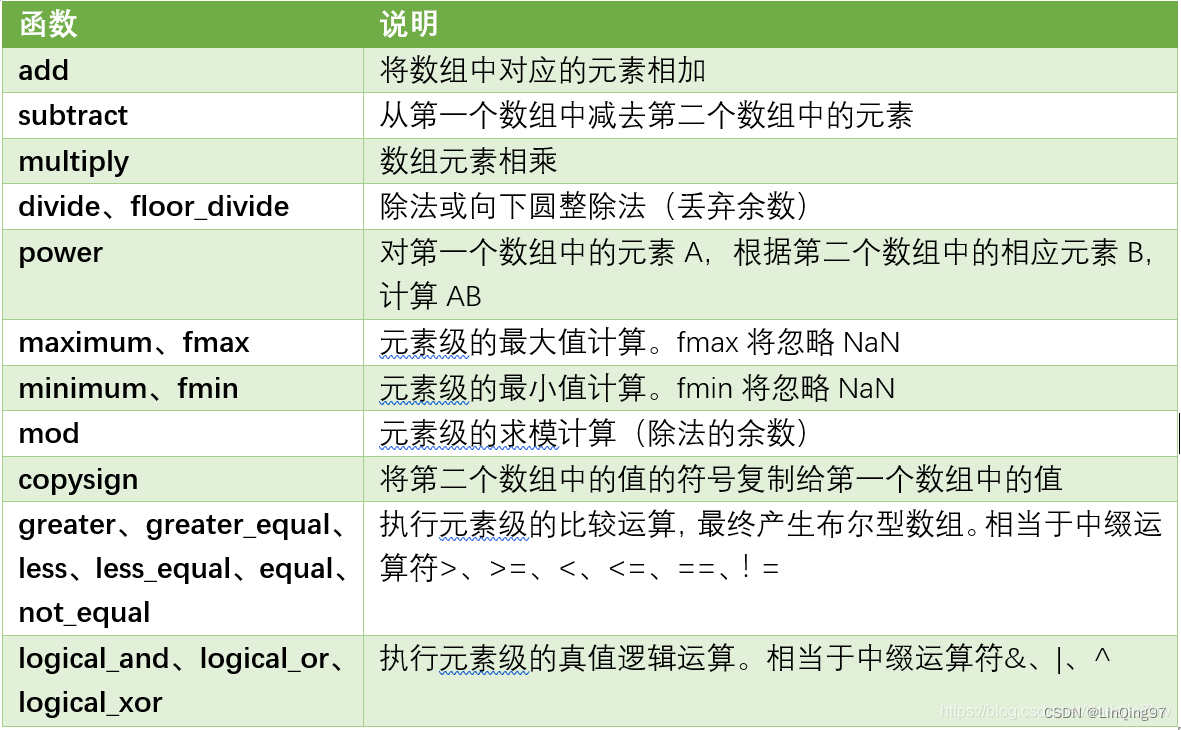

print('二元ufunc示例')
x = np.array([[1, 4], [6, 7]])
y = np.array([[2, 3], [5, 8]])
print(np.maximum(x, y))  # [[2,4],[6,8]]
print(np.minimum(x, y))  # [[1,3],[5,7]]

3.where函数

np.where(condition,x,y)，第一个参数为布尔数组，后两个参数可以为标量也可以为数组

满足条件输出x，否则输出y

print('where函数的使用')
cond = np.array([True, False, True, False])
x = np.where(cond, -2, 2)
print(x)  # [-2  2 -2  2]
cond = np.array([1, 2, 3, 4])
x = np.where(cond > 2, -2, 2)
print(x)  # [ 2  2 -2 -2]
y1 = np.array([-1, -2, -3, -4])
y2 = np.array([1, 2, 3, 4])
x = np.where(cond > 2, y1, y2)  # 长度须匹配
print(x)  # [1,2,-3,-4]

print('where函数的嵌套使用')
y1 = np.array([-1, -2, -3, -4, -5, -6])
y2 = np.array([1, 2, 3, 4, 5, 6])
y3 = np.zeros(6)
cond = np.array([1, 2, 3, 4, 5, 6])
x = np.where(cond > 5, y3, np.where(cond > 2, y1, y2))
print(x)  # [ 1.  2. -3. -4. -5.  0.]

八.ndarray常用统计方法

print('np的基本统计方法')
x = np.array([[1, 2], [3, 3], [1, 2]])  # 同一维度上的数组长度须一致
print(x.mean())  # 2
print(x.mean(axis=1))  # 对每一行的元素求平均
print(x.mean(axis=0))  # 对每一列的元素求平均
print(x.sum())  # 同理 12
print(x.sum(axis=1))  # [3 6 3]
print(x.max())  # 3
print(x.max(axis=1))  # [2 3 2]
print(x.cumsum())  # [ 1  3  6  9 10 12]
print(x.cumprod())  # [ 1  2  6 18 18 36]

用于布尔数组的统计方法

        sum：统计数组/数组某一维度中True的个数

        any：统计数组/数组某一维度中是否存在一个/多个True

        all：统计数组/数组某一维度中是否都为True

print('用于布尔数组的统计方法')
x = np.array([[True, False], [True, False]])
print(x.sum())  # 2
print(x.sum(axis=1))  # [1,1]
print(x.any(axis=0))  # [True,False]
print(x.all(axis=1))  # [False,False]

使用sort对数组/数组某一维度进行排序（会修改数组本身）。

print('.sort的就地排序')
x = np.array([[1, 6, 2], [6, 1, 3], [1, 5, 2]])
x.sort(axis=1)
print(x)  # [[1 2 6] [1 3 6] [1 2 5]]
# 非就地排序：np.sort()可产生数组的副本

九.ndarray数组的去重以及集合运算

print('ndarray的唯一化和集合运算')
x = np.array([[1, 6, 2], [6, 1, 3], [1, 5, 2]])
print(np.unique(x))  # [1,2,3,5,6]
y = np.array([1, 6, 5])
print(np.in1d(x, y))  # [ True  True False  True  True False  True  True False]
print(np.setdiff1d(x, y))  # [2 3]
print(np.intersect1d(x, y))  # [1 5 6]

十.numpy中的线性代数

print('线性代数')
import numpy.linalg as nla

print('矩阵点乘')
x = np.array([[1, 2], [3, 4]])
y = np.array([[1, 3], [2, 4]])
print(x.dot(y))  # [[ 5 11][11 25]]
print(np.dot(x, y))  # # [[ 5 11][11 25]]
print('矩阵求逆')
x = np.array([[1, 1], [1, 2]])
y = nla.inv(x)  # 矩阵求逆（若矩阵的逆存在）
print(x.dot(y))  # 单位矩阵 [[ 1.  0.][ 0.  1.]]
print(nla.det(x))  # 求行列式

十一.numpy随机数生成

import numpy as np
a=np.random.randint(0,10,100)#范围内的整数
print(a)
b=np.random.rand(40)#0到1的均匀分布
print(b)
c=np.random.randn(10)#标准正态分布
print(c)
d=np.random.normal(0,1,100)#生成指定正态分布
print(d)
e=np.random.random(20)#0到1的均匀分布
print(e)
f=np.random.ranf(20)#0到1的均匀分布
print(f)
g=np.random.uniform(-1,1,100)#指定均匀分布
print(g)

十二.numpy数组重塑

print('ndarray数组重塑')
x = np.arange(0, 6)  # [0 1 2 3 4]
print(x)  # [0 1 2 3 4]
print(x.reshape((2, 3)))  # [[0 1 2][3 4 5]]
print(x)  # [0 1 2 3 4]
print(x.reshape((2, 3)).reshape((3, 2)))  # [[0 1][2 3][4 5]]
y = np.array([[1, 1, 1], [1, 1, 1]])
x = x.reshape(y.shape)
print(x)  # [[0 1 2][3 4 5]]
print(x.flatten())  # [0 1 2 3 4 5]
x.flatten()[0] = -1  # flatten返回的是拷贝
print(x)  # [[0 1 2][3 4 5]]
print(x.ravel())  # [0 1 2 3 4 5]
x.ravel()[0] = -1  # ravel返回的是视图（引用） 
print(x)  # [[-1 1 2][3 4 5]]
print("维度大小自动推导")
arr = np.arange(15)
print(arr.reshape((5, -1)))  # 15 / 5 = 3