codeforces 1012B 题解(建图，思维，并查集)

最新推荐文章于 2022-04-26 22:50:14 发布

原创最新推荐文章于 2022-04-26 22:50:14 发布 · 366 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#题解

Codeforces 专栏收录该内容

34 篇文章

订阅专栏

博客围绕矩阵位置确定问题展开，给定大小为n*m的矩阵，其中k个位置已确定，还可通过特定规则确定其他位置。需人工确定一些位置使全部位置确定，求最小人工确定数。介绍了输入输出格式和样例，思路是用并查集合并行和列，计算联通块数量，得出还需连的边数。

原题链接：
洛谷：点我QωQ
CF：点我QωQ

题意简述

给定一个矩阵，大小为 $n * m$ 。其中有 $k$ 个位置被确定了。当然，也珂以通过这样的方式确定：
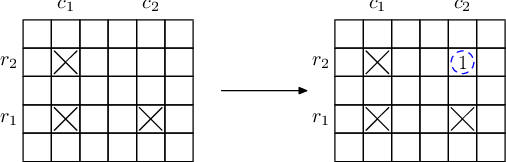
如果 $r_1,c_1),(r_1,c_2),(r_2,c_1)$ 被确定了，那么 $r_2,c_2)$ 也被确定了。

在这 $k$ 个位置确定后，你要人工确定一些位置使得全部被确定。求最小人工确定数。

数据

输入

第一行 $n, m, k$ ( $n, m < = 2 e 5, k < = m i n (n, m)$ )
接下来 $k$ 行，每行一个 $(x, y)$ ，表示位置 $(x, y)$ 被确定了

输出

最小的人工确定数。

样例

输入
2 2 3
1 2
2 2
2 1
输出
0

输入
1 5 3
1 3
1 1
1 5
输出
2

输入
4 3 6
1 2
1 3
2 2
2 3
3 1
3 3
输出
1

思路

我们如何维护上面说的， $(r 1, c 1), (r 1, c 2), (r 2, c 1)$ 都被确定时， $(r 2, c 2)$ 也被确定了？

而且，观察到， $n, m$ 都很大， $O (n m)$ 的算法不可取。然后我们就有一个好想法：把行和列的编号看作点，对于一个给定的点 $(a, b)$ ，并查集合并第 $a$ 行和第 $b$ 列。这样的时空复杂度是 $O (n + m)$ 的！

验证一下上面说的， $r 1, c 1$ 连一条边， $r 1, c 2$ 连一条边， $r 2, c 1$ 连一条边，此时我们发现， $r 2 - > c 1 - > r 1 - > c 2$ ，所以 $r 2, c 2$ 也是联通的！

目标状态就是所有点都被确定了，也就是要让所有点都联通。假设现在我们有 $c n t$ 个联通块，把每个联通块看作一个点，那连出一颗树就能全部联通了。这时候还需要连的边数就是 $c n t - 1$ 。

代码

#include<bits/stdc++.h>
using namespace std;
namespace Flandle_Scarlet
{
    #define N 400100
    class DSU//并查集
    {
        public:
            int Father[N],Cnt[N];
            void Init()
            {
                for(int i=0;i<N;i++)
                {
                    Father[i]=i;
                    Cnt[i]=1;
                }
            }
            int Find(int x)
            {
                return (x==Father[x])?x:(Father[x]=Find(Father[x]));
            }
            void Merge(int x,int y)
            {
                int ax=Find(x),ay=Find(y);
                if (Cnt[ax]<Cnt[ay])
                {
                    Cnt[ay]+=Cnt[ax];
                    Father[ax]=ay;
                }
                else
                {
                    Cnt[ax]+=Cnt[ay];
                    Father[ay]=ax;
                }
            }
    }D;
    
    int n,m,k;
    #define R(x) x
    #define C(x) x+n
    //通过+n的方式区别开R和C
    void Input()
    {
        scanf("%d%d%d",&n,&m,&k);
        for(int i=1;i<=k;++i)
        {
            int u,v;
            scanf("%d%d",&u,&v);
            D.Merge(R(u),C(v));//建立初始连边
        }
    }

    void Solve()
    {
        int cnt=0;
        for(int i=1;i<=n+m;++i)
        {
            if (D.Find(i)==i) ++cnt;
            //说明i是根节点
            //在并查集中，一个根节点唯一对应一个联通块
            //所以，联通块个数=根节点个数
        }
        printf("%d\n",cnt-1);//求个数,-1
    }

    void Main()
    {
        if (0)
        {
            freopen("","r",stdin);
            freopen("","w",stdout);
        }
        D.Init();
        Input();
        Solve();
    }
};
main()
{
    Flandle_Scarlet::Main();
    return 0;
}