HDU 6370 Werewolf 题解（并查集+图论+DFS）

原链接
点我QωQ

题意简述

一群人玩♂游♂戏。游戏中有两种人，村民和狼人，村民只会说真话，狼人随便（真或假均珂）。给定一些关系，表示第$i$个玩家说第$j$个玩家是狼人/村民。请分别找出确定是村民/狼人的个数。

数据

输入

多组数据。第一行是一个$T$，表示有$T$组数据。每组数据中有一个$n(n<=10^5)$，表示有多少人。接下来$n$行，第$i$行有一个正整数$x$和一个字符串$s$。如果$s="villager"$，则表示$i$说$x$是村民；如果$s="werewolf"$，表示$i$说$x$是狼人。保证$i$ ≠ $x$。

输出

对于每组数据，输出两个用空格隔开的整数，表示确定是村民的个数，和确定是狼人的个数。

样例

输入
1
2
2 werewolf
1 werewolf
输出
0 0

思路

（有一个背景，就是你要想到一个人说别人是狼人/村民的这个关系珂以看成一个图。。。要注意到这一点,不然下面不太好讲。。。如果注意到了，那你一定是巨佬）
我们知道，狼人是随便说的，即使全部是狼人也不会有问题。所以第一个数一定输出$0$，每个人都珂以成为狼人，不珂能确定一个人是村民。
接下来就是如何求那些确定是狼人的个数了。现在，我们要想想，什么时候珂以确定一个狼人？珂以从反面思考：如果某个人是村民，那么就会通过一些连锁反应得到这个人是狼人，这个人就一定是狼人了。如果对构造这一块比较懂的话（这可是一个重要的技巧，在虽然呈现在结果形式很少，但作为过程推理尤为重要），一会就能凑出来一种情况：“连环村民”。如下例：
$n=3$
$2$ $villager$
$3$ $villager$
$1$ $werewolf$

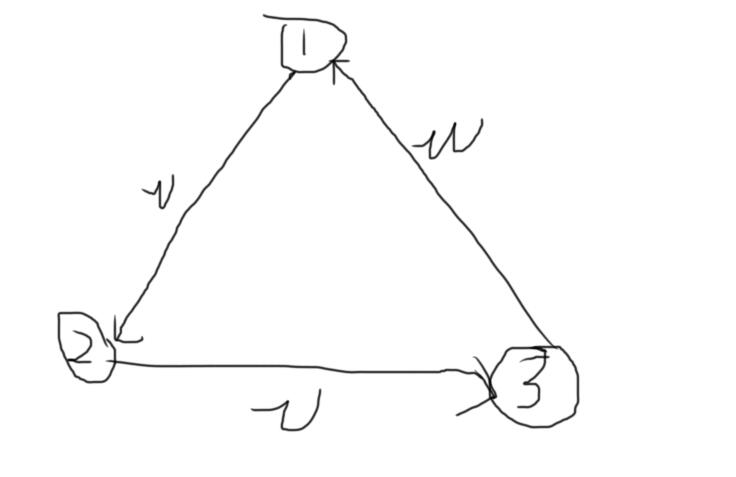
如果$1$是村民，那么珂以推出，$2,3$也都是村民，但是由于$3$是村民，所以说真话，也就会得到：$1$是狼人。就矛盾了(刚刚才说$1$是村民来着)，所以$1$不能是村民。

这样我们就确定了$1$肯定是狼人。（顺便说一句，这个"连环村民"的关系珂以用并查集求出）那么，还有那些珂能是狼人呢？
在这个例子中，仿佛没了。我们再加一个点。

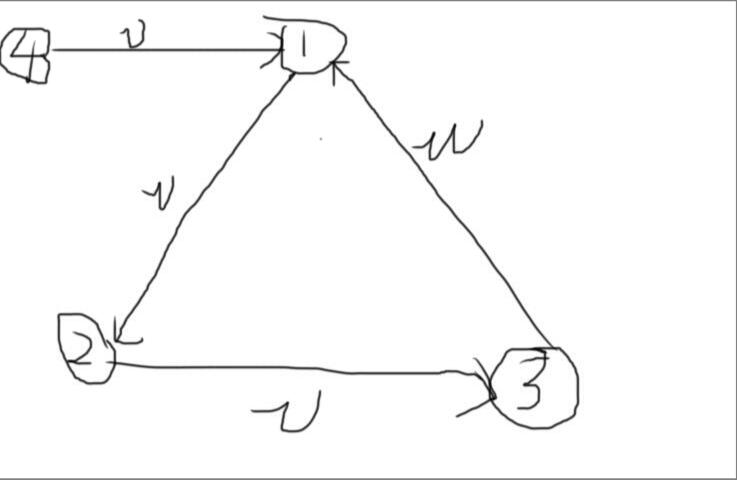
我们会发现，点$4$肯定不是村民，因为村民一定说真话。已知$1$是狼人，如果$4$说的是对的，那么$1$就是村民了，所以$4$肯定要说假话，即$4$是狼人。广义一下，也就是：

以一个村民边连向一个狼人的点是狼人。

这样我们就珂以由一个狼人确定另一个狼人，在由新确定的这个狼人再确定一个狼人$\cdots$，直到确定不了为止。这一步用$DFS$实现。当然，我们是要往回找，所以在输入的时候，要建一个反边。

代码：

#include<bits/stdc++.h>
using namespace std;
namespace Flandle_Scarlet
{
    #define N 100100
    class DSU//并查集(带按秩合并+路径压缩)
    {
        public:
            int Father[N],Cnt[N];
            void Init()
            {
                for(int i=0;i<N;++i)
                {
                    Father[i]=i;
                    Cnt[i]=1;
                }
            }
            int Find(int x)
            {
                if (x!=Father[x]) Father[x]=Find(Father[x]);
                return Father[x];
            }
            void Merge(int x,int y)
            {
                int ax=Find(x),ay=Find(y);
                if (Cnt[ax]<Cnt[ay])
                {
                    Cnt[ay]+=Cnt[ax];
                    Father[ax]=ay;
                }
                else
                {
                    Cnt[ax]+=Cnt[ay];
                    Father[ay]=ax;
                }
            }
            bool Query(int x,int y)
            {
                return Find(x)==Find(y);
            }
    }D;

    int Wolf[N][2];int cntw=0;//保存狼人边
    vector<int>Man[N];//保存村民边
    //说一下两种边为什么写法不同。因为我们在遍历狼人边的时候，并不需要维护类似"某个点连出去一些边"的关系，一个起点多个终点的形式并没什么用，我们只要最快的知道所有起点和终点，自然就是写数组了。
    //但是村民边就不一样了。我们要知道一个点连向多个点的关系，这十分重要，所以要用vector存
    int n;
    void Input()
    {
        for(int i=1;i<=N;++i)
        {
            Man[i].clear();
            Wolf[i][0]=Wolf[i][1]=0;
        }cntw=0;//初始化

        scanf("%d",&n);
        for(int i=1;i<=n;++i)
        {
            int x;char tmp[20];
            scanf("%d%s",&x,tmp);
            if (tmp[0]=='v')//村民边
            {
                Man[x].push_back(i);//记得存反边
                D.Merge(i,x);
            }
            else//狼人边
            {
                ++cntw;
                Wolf[cntw][0]=i,Wolf[cntw][1]=x;
            }
        }
    }

    int ans=0;
    void DFS(int x)
    {
        for(int i=0;i<Man[x].size();++i)
        {
            ++ans;//说明Man[x][i]也是一个狼人，所以++ans
            DFS(Man[x][i]);//继续遍历Man[x][i]，看它还能确定哪些狼人
        }
    }
    void Solve()
    {
        ans=0;
        for(int i=1;i<=cntw;++i)
        {
            int u=Wolf[i][0],v=Wolf[i][1];
            if (D.Query(u,v))
            //"连环村民"
            //两个点被一连串的村民边间接连接，但是中间有一个狼人边直接连接
            //我们知道，此时，这个狼人边的终点肯定是一个狼人
            {
                ++ans;//所以++ans
                DFS(v);//从终点开始用DFS确定点
            }
        }
        printf("0 %d\n",ans);
    }

    void Main()
    {
        if (0)
        {
            freopen("","r",stdin);
            freopen("","w",stdout);
        }
        int T;scanf("%d",&T);
        while(T-->0)
        {
            D.Init();
            Input();
            Solve();
        }
    }
};
main()
{
    Flandle_Scarlet::Main();
    return 0;
}

回到总笔记界面