基于重写系统的隐私保护聚类

基于树的分类聚类算法中的隐私感知数据共享

1 引言

聚类是无监督数据分析中一种广为人知的工具，在不同领域都受到了大量研究关注，涵盖信息检索、文本挖掘、科学数据分析以及医学诊断[1]。聚类指的是将一组数据点划分为若干组的过程，使得同一组内的元素彼此之间的相似性高于与其他组中元素的相似性。尽管聚类算法在广泛应用中具有显著优势，但极少有研究工作使用形式化方法来表达和解决聚类算法的问题[13]。

在本研究中，我们采用一种名为CCTree的分类聚类算法的抽象表示[12],来形式化分布式聚类。当数据最初在不同站点收集时，主要应用分布式聚类[6]。通常，为了全局效益，分布式代理希望获得整个数据上的全局聚类结构，但出于隐私问题，他们不愿意共享自己的数据集，除非能够保证所需的隐私级别[2]。例如，疾病控制中心（主代理）希望利用不同医院（代理）中患者记录的聚类结果来识别疾病趋势与模式。整个数据集的结果有助于所有代理找到更好的治疗方法。然而，由于隐私顾虑，医院不愿披露患者记录，除非满足一定的隐私级别[9]。

在本研究中，我们解决了隐私感知的分布式CCTree聚类问题。为此，首先每个智能体使用CCTree算法[12]对其自身的数据集进行聚类。然后，每个智能体将聚类的抽象结构发送给主代理（诚实但好奇）。如果聚类的抽象模式能够保护数据持有者的所需隐私，则该抽象模式将被发布。主代理聚合各聚类结果以获得CCTree的全局结构，使得每个智能体都能够基于该全局结构使其自身聚类同质化。主代理执行的整个过程通过重写系统进行形式化。重写系统作为一种成熟的数学结构，通过应用正确指定的规则[3]自动产生新的期望最终结果。

本文的贡献可以总结如下：
– 提供了两个重写系统，以自动验证代数结构中的元素是否符合CCTree结构，并且能够从分布式代理收集的CCTree抽象模式中自动生成全局CCTree结构。
– 我们证明了所提出的重写系统具有终止性并产生唯一结果。此外，我们指出了在何种条件下，我们的分布式CCTree聚类结果可与集中式方法的结果进行比较。
– 提供了一种度量方法，供数据持有者衡量在公开其数据的CCTree结构后获得的隐私增益，以决定是否参与数据共享。

本文组织如下。在第2节中，提供了所提出方法论所需的背景知识。在第3节中，我们应用抽象CCTree表示，通过重写系统来形式化CCTree分布式聚类。在第4节中，我们对文献进行了回顾。我们在第5节中总结并指出了研究的未来方向。

2 背景

在本节中，我们提供一些所需的基础信息。

2.1 CCTree 构建

CCTree[12]通过类似决策树的结构迭代构建，其中树的叶节点即为所需的簇。CCTree的根节点包含所有待聚类的元素。每个元素通过一组类别型属性进行描述。由于是类别型属性，每个属性只能取有限个离散值，这些值构成其域。在每一步中，当上一层的节点不够均匀时，将对其进行拆分，从而生成树的新层级。香农熵既用于定义一种称为节点纯度的均匀性度量，也用于选择用于拆分节点的属性。具体而言，非叶节点通过使香农熵达到最大值的属性进行划分。该划分通过对应于该属性各个可能取值的分支来表示。从父节点引出的每条分支或边都标记有选定的特征，用以指导数据流向子节点。当一个节点满足以下任一停止条件时，即被视为叶节点：(1) 元素数量少于阈值“μ”，或 (2) 节点纯度优于“ε”。图1展示了一个简单的CCTree。

2.2 重写系统

重写规则是项的有序对，记作 x → y，其中包含项 x和 y。类似于等式，规则用于将 x的实例替换为对应的 y实例。与等式不同的是，规则不会用于替换右侧 y[3]的实例。在符号集G、常量K和变量X上的项要么是变量 x ∈X，要么是常量 k ∈K，要么是形如 g(t1, t2, … , tn)的表达式，其中 g ∈ G是一个具有 n个参数的函数符号，而 ti是项[3]。对于规则“→”的一个推导是一个形如“t0 → t1 →…”的序列。如果存在一个元素 u使得“t → u”，则称元素t是可约的（相对于 →）；否则被认为是不可约的。重写系统 R是一组重写规则 t → u，其中 t和 u是项。项 u是 t的“→范式”。

如果“t →∗ u”和 u通过 →是不可约的，其中“→∗”表示连续应用转移。一个关系 →是终止的，如果没有无限推导“t0 → t1 →…”，这意味着它不会到达一个范式项。一个关系 →是合流的，如果存在一个元素 v，使得当“u →∗ s”和 “u →∗ t”对某些元素 s、 t和u成立时，有“s →∗ v”和“t →∗ v”。一个关系 →是收敛的，如果它是终止的且合流的。收敛重写系统具有重要意义，因为所有推导都会导向唯一的范式[3]。条件规则是一种等式蕴含，其中结论中的项是有方向的。我们使用形式“x1= u1 ∧… ∧ xn= un | x → y”来表示在条件“x1= u1 ∧… ∧ xn= un”下可得“x → y”。

2.3 特征簇代数

在本节中，我们介绍[13]中提出的特征簇代数，该代数通过项对CCTree表示进行抽象。我们在[13]中证明了，在特征集存在序的条件下，所提出的项完全抽象CCTree结构。完全抽象保证了CCTree结构与其对应的CCTree项可以相互替代使用。接下来，我们将简要介绍本研究中将使用的CCTree抽象的符号表示[13]。

（I）特征半环：假设给定一组互不相交的属性，记为 A，其中每个属性 Ai ∈ A 的载体集记为 VAi。我们将所有属性的并集，记为 V=⋃Ai∈A VAi，称为值集或特征集。例如，属性集可以是 A ={color, size}，其中 Vcolor={red, blue}，且 Vsize={small, large}。因此，特征集等于 V={red, blue, small, large}。

令 F= P (P (V)) 表示 V 的幂集的幂集。我们记 1={∅} ∈ F 和 0= ∅ ∈ F，并在 F 上分别定义运算“+” 和“·” 为“Fi+ Fj= Fi ∪Fj” 和“ Fi · Fj={Xs ∪ Yt: Xi ∈ Fi, Yt ∈ Fj}”，其中 Fi, Fj ∈ F[13]。于是，当 F 属于 F 时，它满足以下语法形式之一： F:= 0 | {{f}}| F · F | F+F | 1，其中 f ∈ V。此时，五元组(F,+,·, 0, 1) 构成一个交换半环。

(II) 元素的半环：假设给定属性集 A ={A1, A2,…, Ak}。我们说 s 属于元素集合 S，如果 s ∈VA1 ×VA2 ×… ×VAk × N，其中 N 是自然数集。因此，s ∈ S 可表示为 s=(x1, x2,···, xk, n)，其中 xi ∈V Ai 对于 1 ≤ i ≤ k 成立，且 n ∈ N 表示一个元素的标识符。为了简便起见，我们可以使用替代表示 xi ∈ Ai 来代替 xi ∈ V Ai。在我们的问题中，S 是所有希望进行聚类的元素的集合。由于在分布式聚类中存在不同的待聚类元素集合，我们如下定义所有元素幂集的半环。在P(S)（即 S 的幂集）的元素上定义两个运算“+” 和“·”，分别对应“Si+ S j = Si ∪ S j ” 和“Si · Sj = Si ∩ S j ”，其中 Si, Sj ∈ ∈ P(S)。形式上，我们称 S 属于元素集合 S ∈ P(S)，如果它满足以下语法形式之一：

S：= ∅| S′ | S+ S | S · S | S，其中 S′ ⊆ S。那么，五元组（S+，·， ∅， S）是一个交换半环[13]。

定义1（特征簇（族）项） 。关于 V和 S的特征簇族项集合，记为FCV,S（或在上下文明确时简记为 FC），是最小的满足以下条件的元素集合：

if S ⊆ S then S ∈ FC
if F ∈ F1, S ⊆ S then F S ∈ FC
if τ1 ∈ FC, τ2 ∈ FC then τ1+ τ2 ∈ FC

在这种情况下，我们将 S和 F S称为特征簇项，而一个或多个特征簇项的加和称为特征簇族项。我们可以简单地使用 FC-项来指代一个特征簇族项。我们定义了块函数，该函数接收一个 FC-项，并返回其块的集合，如下所示：

block: FC → P(FC)
block(S)={S}, block(F S)={F S}, block(τ1+ τ2)= block(τ1) ∪ block(τ2)

如果没有特征直接指定 S，则称为原子项。所有原子项的集合记为 A。

定义2（CCTree项） 。由CCTree结构产生，或等价地可转换为CCTree结构的项，称为CCTree项。

示例1 。由图1得到的CCTree项如下所示：

τ= red S+ blue· small S+ blue· large S

其中符号“·”用于分隔指定簇的特征，符号“+”用于分隔不同的簇，而“” 用于表示某个簇来源于哪个主数据集。后一属性在分布式聚类过程中是可取的，因为在分布式聚类中，数据在不同的代理上进行聚类。

定义3（项） 。我们称 τ为一个项，如果它具有以下形式之一：τ：= S | F S | τ+ τ | τ· τ，其中 S：= ∅| S′ | S+ S | S · S | S且 F：= 0 | {{f}}| F+ F | F · F | 1。项的集合在 S和 F上记为C S,F，或简写为 C。

定义4（特征簇代数） 。五元组(C,“+”,“·” 0 ∅,1 S)是一个幂等交换半环，称为特征簇代数。

定义5（序重写规则） 。设给定一个特征的有序集(V,<)。一个 FC-项称为在(V, <)上的有序 FC-项，如果它是以下重写规则的范式：

f1 · f2 S →O f2 · f1 S if f1< f2 ∀ f1, f2 ∈ V

此外，我们定义了一个重写规则，该规则根据属性 A ∈A对 FC-项的特征进行排序，表示为 f2· f1 S −→AO f1· f2 S，适用于 f1 ∈ A。我们将基于属性 A应用上述重写规则后得到的项 τ的范式表示为 τ ⇓A。

为避免同一 FC‐项的不同表示形式造成混淆，以下将给出因式分解的和未因式分解的项的定义。在所提供的示例中，使用属性 Color={r(ed) b(lue)}、 Size={s(mall) l(arge)} 和 Shape={c(ircle) t(riangle)} 来描述这些项。

定义6（因式分解项） 。我们通过属性 A ∈A定义因式分解重写规则，记为 −→A，将 FC-项重写为其因式分解的形式，如下所示：

f · τ1+f · τ2 −→A f ·(τ1+ τ2) for f ∈ A

我们用τ ↓A表示在项τ上通过属性 A应用因式分解重写规则后的范式，FC的因式分解形式集合记为 FC ↓。经过因式分解后的项称为factorizedterm。

定义7（未因式分解项） 。我们定义在 FC-项上的去因式分解重写规则为“f ·(τ1+ τ2) →d f · τ1+f · τ2”。由去因式分解重写规则得到的正常项称为未因式分解项。项 τ的未因式分解形式记为 τ ↑。 FC中各项的未因式分解形式的集合记为 FC ↑。

示例2 . 对于因式分解，我们有：(r · s S+ r · c S+ b · s S) ↓color=r·(s S+c S)+b·s S，而对于去因式分解，我们得到： r·(s S+c S)+b·s S →dr · s S+ r · c S+ b· s S。

接下来，我们提出一组关于特征簇代数的关系，该代数在[13],中被引入，适用于我们的分布式聚类方法论。

定义8（属性划分） . 属性划分(DA)是一个从A × FC 到{True, False}的函数，它接收一个属性和一个未因式分解的FC-项作为输入；其返回值为True 或False，具体如下：

DA(A, S)= False
DA(A, f S)= True if f ∈ A
DA(A, f S)= False if f∈/ A
DA(A, f · F S)= DA(A, f S)∨ DA(A, F S)
DA(A, τ1+ τ 2)= DA(A, τ1)∧ DA(A, τ2)

属性划分概念用于对项中出现的属性进行排序。

定义9（初始） 。我们定义从P(FC ↑)到P(F)的初始(δ)函数，该函数接收在(V, <)上的一组有序非因式化项，并返回每个项的第一特征集合，如下所示：

δ(∅) ={0}, δ({S}) ={1}, δ({f · F S}) ={f}, δ({τ1+ τ2}) = δ({τ1}) ∪δ({τ2})

当输入集合仅包含一个项时，我们去掉括号，即δ({τ})= δ(τ)当 |{τ}| = 1。此外，当输出集合也仅包含一个元素时，为了简化，我们同样去掉括号，即 δ(X)={f}=f对于 X ∈P(FC ↑)。初始函数将在评估某一项是否表示CCTree项的过程中使用，考虑到在CCTree中，兄弟节点特征（有序项中的第一特征）属于同一属性。

定义10（导数） 我们定义导数，记为 ∂，是一个函数，它接受一个在(V,<)上的有序未因式分解的 FC-项，即 ∂: FC ↑→P(FC)；其返回通过截去第一特征得到的项（项的集合），如下所示：

∂(S)= ∅, ∂(f S)={S}, ∂(f · F S)={F S}, ∂(τ1+ τ2)= ∂(τ1)∪ ∂(τ2)

导数函数被定义用于评估一个项是否表示CCTree项的过程。更准确地说，如果一个有序项中的第一层特征（树中的兄弟节点）属于相同的属性，则通过导数函数去除第一特征，以评估子项（子树）是否也表示CCTree项。

注意，函数initial(δ)和derivative(∂)根据输入内容（即输入是树还是项）对输入进行了重载。

定义11（属性顺序） 我们称属性 B在未因式分解项 τ ∈ FC ↑上小于或等于属性 A，记作 B τ A,，如果 τ所划分的块的数量少于（或等于） B所划分的块的数量。形式上， B τ A意味着：

|{τi ∈ block(τ)| DA(B, τ i )= T rue}| ≤ |{τi ∈ block(τ)| DA(A, τ i )= T rue}|

给定一组属性A和一个项 τ，集合(A τ)是一个格。我们将此集合的上界表示为A,τ。这意味着我们有 ∀ A ∈A⇒ A τ A,τ。

例3 . 接下来我们展示如何确定一个项的属性序。假设给定项 τ= r · s S+ r · c S+ b· s S。我们有：block(τ) ={r · s S, r · c S, b· s S}。因此，我们得到：

|{τi ∈ block(τ)|DA(shape, τi)= T rue}| = 1
≤ |{τi ∈ block(τ)|DA(size, τi)= T rue}| = 2
≤ |{τi ∈ block(τ)| DA(color, τi)= T rue}| = 3

这意味着我们有“shape τ size τ color”。即，属性“color”是出现在 τ项的所有块中的那个属性。我们注意到，在CCTree中，从根开始的第一个属性就是在对应CCTree项所有块中出现的属性。例如，在示例1的CCTree项中，颜色属性存在于所有块中。

特征排序。 回想一下，如果特征之间没有预定义的序，则会在项的完全抽象中产生问题[13]。为此，我们提出一种对特征集进行排序的方法，该方法适用于我们的问题。给定一个 FC‐项 τ，我们根据定义11来确定属性的序；而当对于任意两个属性 A和 A′，若存在 A= A′，则在不失一般性的情况下，我们在它们之间选择一个严格序，例如 A ≺ A′。然后，在每个属性中，我们任意地（并固定）对特征进行排序。

定义12（有序合一） 。有序合一（F）是从P（A） × FC ↑到 FC ↓的一个偏函数，其接收一组属性和一个未因式分解项；根据所接收项中属性的顺序，迭代地返回重写规则的范式 −→AO（定义5），具体如下：

F(∅, τ ↑)= τ, F({A}, τ ↑)= τ ⇓A, F(A, τ)= F(A,τ, F(A −{A,τ}, τ ↑))

有序合一的范式称为统一项。F ∗(τ)表示对 τ上的有序属性集迭代执行F以得到统一项。

Orderedunification function 通过自动排列项的特征，如前所述，可引导项的形状，以便轻松验证其是否为CCTree项。

示例4 。 为了找到 τ1= r · s S+ r · c S+ b · s S的统一形式，我们有：

F ∗(τ1)= F({shape, color, size}, τ1 ↑)= F(color, F(size, F(shape, τ1)))
= r · s S+ r · c+b· s S

定义13（良构项） 。良构函数，记为 W，是从 FC ↑到{True, False}的二元函数，其接收一个统一的未因式分解的FC-项 τ ↑；若 δ(τ ↑)等于A中某个属性，则返回True；否则返回False。形式化地：

W(τ ↑)={True if ∃ Ai ∈ A s.t. δ(τ ↑)= Ai
False otherwise

如果 W(τ)= T rue，则称统一项 τ 为 结构良好的术语。

原子项被视为一个结构良好的术语。基本上，结构良好函数用于验证在一个统一的未因式分解项中，一级特征是否属于同一属性，符合CCTree结构的要求。

定理1 。一个统一项表示一个CCTree项，或者可转换为CCTree结构，当且仅当：(1) 它可以写成形式 F ∗ (τ)=∑i fi·τi，使得 (1) “W(F ∗ (τ))= T rue”，即该接收项的统一形式是一个结构良好的术语；并且 (2) 每个 τ i的统一形式也是一个结构良好的术语 (W(τi)= T rue)，以及 (3) 每个 τ i满足上述要求[13]。

3 分布式私有CCTree聚类

数据聚类在从分子生物学到市场营销的广泛应用中正变得越来越重要[1]。在许多领域，数据是在不同的站点收集的，例如不同的医院。由于隐私问题，每个数据持有者可能会阻止发布自己的数据集，除非能保证一定的隐私级别[9]。为此，每个参与智能体通过比较发布聚类算法结果与发布原始数据集时的隐私泄露量来计算隐私泄露程度。如果该差值高于其期望的阈值，则她将共享自己的CCTree；否则，她拒绝参与协作构建CCTree。

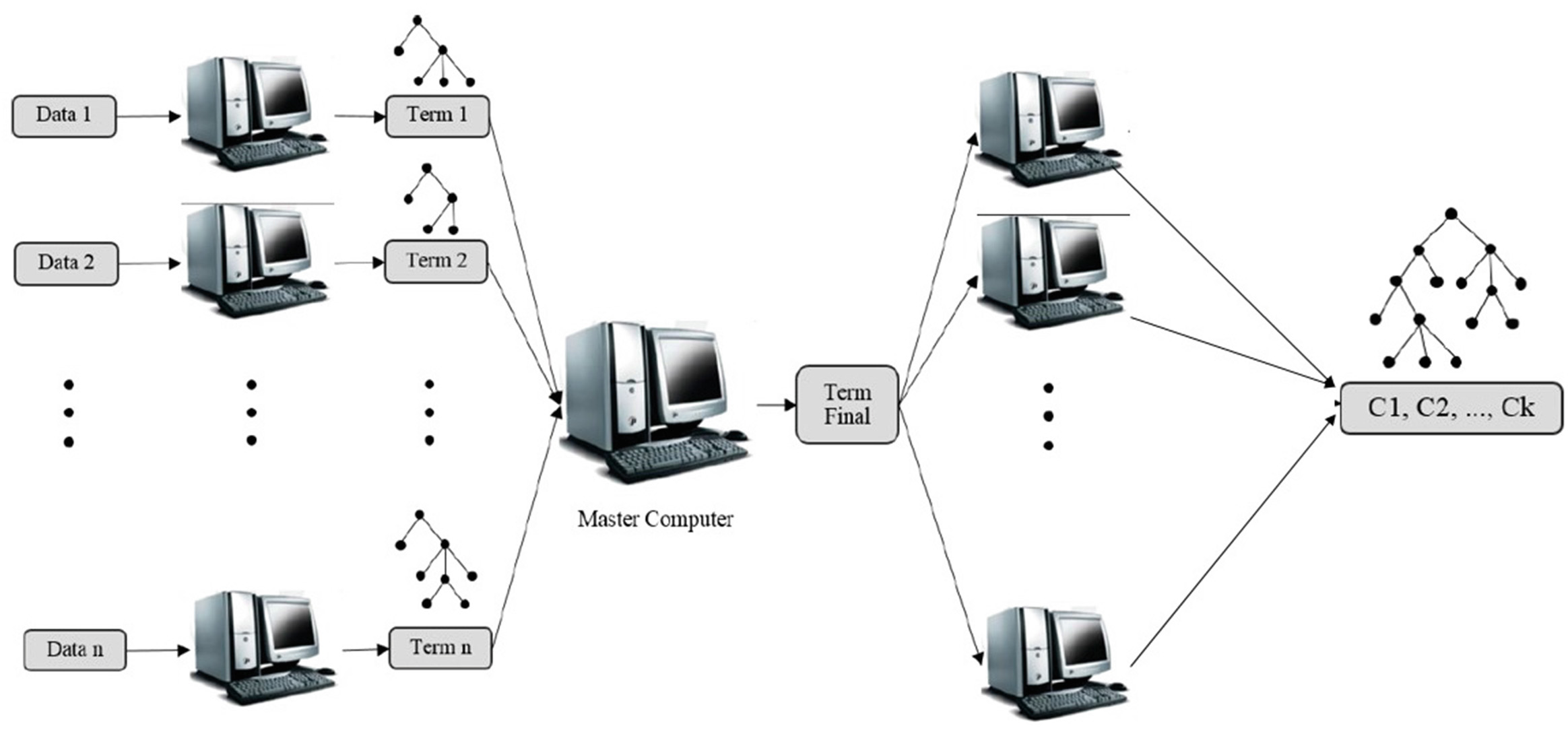
随后，每个参与智能体中每个CCTree的结果被转换为其等效的CCTree项。生成的CCTree项被报告给主代理（诚实但好奇）以进行组合。CCTree项根据我们提出的组合重写规则（表2）自动组合，从而生成一个所有项均可同质化到的最终CCTree项。因此，将组合结果报告给各个智能体以同质化CCTree项，进而同质化所有CCTree的结构。图2描绘了该架构的高层表示。

接下来，我们首先证明，如果所有代理将CCTree的停止条件（叶子中元素的最小数量）固定为 μ，则将结果发布为CCTree项可满足k‐匿名数据集（k依赖于 μ）[4]。然后，我们提出CCTree重写系统，用于自动验证一个项是否符合CCTree结构。接着，我们提出了组合重写系统，该系统用于通过多个CCTree项的合并（来自分布式代理）来找到一个全局CCTree项。在本节最后，我们证明了所提出的方法论能够实现：（1）从多个CCTree项的合并中得到唯一的CCTree项；（2）寻找全局CCTree的过程能够终止；（3）时间复杂度得到改善与集中式方法相比的分布式系统，最后（4）在某些条件下，由分布式架构生成的CCTree可与集式模式相媲美。

3.1 隐私感知数据共享

在[5],中提出了一种统计框架，用于衡量通过发布分类器结果所导致的隐私侵犯程度。我们将相同的符号体系扩展到我们聚类算法结果的发布场景中。该隐私侵犯形式化地定义如下：给定一个分布(P, U, S)，其中 P是包括攻击者在内的所有人都可访问的公开数据， S是我们试图保护的敏感数据，而 U是攻击者未知的数据。CCTree产生的结构，即 C（CCTree项），对攻击者是可获取的，攻击者可利用其在给定 P的情况下预测 U。假设已有t个样本({,p1)…,( s1,pt) st被攻击者掌握。目标是检验披露所产生的}是否会增强攻击者对未见样本的 C值的预测能力。期望的结果是 S的预测精度不会明显高于随机猜测，且攻击者无法通过应用 C来提升自身对 S的估计能力。从形式上讲，这一概念通过贝叶斯误差来度量，意味着对于所有使用 C的分类器，其贝叶斯误差应与所有使用(P,P( C))的分类器的贝叶斯误差相同。具体而言，给定P和来自 C与 t的样本，若 P( S) ρ;t,= ρ{t以及 P(S}; ρ)t; C,= ρ{t(P) C分别为仅使用P和使用 S}, P ( P)的分类器的贝叶斯误差，并令 ClimP，且 ρ¯=(t→∞) ρ¯limC(=;t→∞ ρ)，则得到来自t的如下定义。

对于 0 ≤ p ≤ 1，CCTree C的结果是(t,p)隐私违规的，如果 ρ(t; C) ≤ρ(t) −p；而聚类 C是(∞,p)‐隐私违规的，如果 ρ¯(C) ≤ ρ¯ − ρ。

根据此定义，如果一个智能体发现共享她的CCTree会违反其隐私要求，她可以拒绝参与共享基于其数据集生成的CCTree。

3.2 CCTree重写系统

为了能够定义一些规则来验证一个项是否满足CCTree结构，需要先定义项的Component概念。粗略地说，CCTree项的一个组件是指CCTree结构中的子树。因此，当我们需要检查一个项对CCTree结构的合规性时，必须通过子项进行迭代验证，以符合CCTree的迭代结构。

定义14 (组件) . 给定两个有序的未因式分解的 FC-项 τ 1和 τ 2，其定义域为(V,<)，我们定义组件 关系（用 ∼ 表示）为项的第一层比较，即 τ 1 ∼ τ 2 ⇔ δ(τ1)= δ(τ2)。

设有序项 τ ∈ FC ↑在(V,<)上给出。τ ′ ∈ block(τ)的等价类称为 τ的一个组件，其形式化定义如下：

[τ′]τ={τi ∈ block(τ) | τ′ ∼ τi}

项 τ通过等价关系 ∼的所有组件的集合，记作“block(τ)/∼”或简记为“τ/∼”，即我们有： τ/∼={[τi]τ | τi ∈block(τ)}。

我们根据 V 中特征的顺序对项 τ 的组件进行排序，如下所示：

[τ′]τ<[τ′′]τ ⇔ ( ∀f′ ∈ δ([τ′]), ∀ f′′ ∈ δ([τ′′]) ⇒ f′< f′′)

由于特征是严格有序的，组件也是严格有序的。

示例5 。 考虑τ1在示例4中的项的有序形式，即 τ1=r · s S+ r · c S+ b· s S。 τ1 ↑的组件为{r · s S, r · c S}（所有块均以 r开头）和{b· s S}（所有块均以 b开头）。此外，若在第一特征序中有 r> b，则{r · s S, r · c S}>{b· s S}。

为了自动验证一个项是否为CCTree项，表1中提供了一组条件重写规则。该表中的项 ∅指的是一个 null项。在此基础上，将CCTree重写系统应用于接收到的项；若最终唯一的不可约项为 ∅，则该项即为CCTree项。在此重写系统中，[[f(τ)]]表示 f(τ)的语义被替换，且结果被视为一个唯一的项。此外， τ1: τ2包含两个项 τ1和τ2，每一项都被视为一个新的项。此外，[τ]i指的是“τ/∼” 的第 i个组件{v56}。

规则	条件	动作
(1) (τ ∈ A) | τ → ∅	-	-
(2) (τ = F ∗(τ)) | τ →[[F ∗(τ)]]	-	-
(3) (τ= F ∗(τ)) ∧(W(τ)) ∧(τ∈/ A) | τ →[[Στ k ∈[τ]1 ∂(τk)]]: ......: [[Στ k ∈[τ]| τ/∼| ∂(τk)]]	-	-

表1中的第一条规则规定，如果一个项是原子项，则将其指向 ∅。第二条规则表明，如果一个项不在统一形式中，则需要转换为其统一表示。第三条规则规定，如果一个非原子统一项是结构良好的，则将其分解为其组件的导数。最后一条规则用于验证CCTree条件是否满足由CCTree的迭代结构产生的后续组件，这些规则遵循定理1的结构，以判断一个项是否符合CCTree结构。

示例6 。 假设给定项 τ 1= a1 S+ b1 S及其属性集合A={a1, a2}, B={b1, b2}。我们应用CCTree重写规则来自动验证 τ 1是否为CCTree项。该项 τ 1不是原子项。此外，我们有 τ 1= F ∗ (τ1)以及“W(τ1) = F alse”，因为第一特征τ1的组件不相等。没有可应用的CCTree重写规则，而该项不是 ∅。这意味着接收到的项 τ1不是CCTree项。

作为另一个示例，我们说明具有属性集 A={a1, a2}, B={b1, b2}的项 τ2= a1 S+ a2 S是一个CCTree项。

(τ2= F ∗(τ2))∧(W(τ2)) | a1 S+ a2 S−(−3→) S: S −(−1→) ∅: ∅

该条件重写规则验证了：如果项处于统一形式，并且在统一形式下所有第一特征属于同一属性或不属于同一属性。如果是，则将该项分解为其组件，以对后续子项验证相同条件。由于移除第一特征后得到的是原子项（即没有特征指定的项），每个原子项都被导向一个null项。除了 ∅之外不存在不可约项，因此 τ2是一个CCTree项。

3.3 组合重写系统

为了解决组合过程，提出了一组组合重写规则（表2），用于在某项不是CCTree项时自动获得CCTree项。将拆分关系（表2的第4条规则）添加到表1的规则中，以从非CCTree项得到CCTree项。

定义15（拆分） 。假设给定一个在（V,<）上的统一项 τ ∈ FC ↑以及属性集合A，考虑A,τ作为 τ的上界属性，我们定义拆分关系如下：

split(τ)={τ if W(τ)= T rue
∑τi∈block(τ) ζ(τi) if W(τ)= F alse

其中：
ζ(τ i )={τi if DA(A, τi)= T rue
(∑a i∈A ,τ ai)· τi if DA(A, τi)= F alse

这意味着 τ中所有不包含A,τ中任何特征的块，都将与A,τ的特征之和相乘。在下面的例子中，我们展示 split关系是如何应用的。

例7 。 假设给定项 τ 2= r · s S+ c S+ b S。我们有 W(r · s S+ r· c S+ b S) = F alse，因此， τ 2不是结构良好的术语。考虑到 A,τ 2 = color，以及DA(colro, r · s S) = T rue, DA(colro, r · c S) = T rue, DA(colro, b S) = F alse，我们得到： split(r · s S+ c S+ b S) =r · s S+(r+ b) · c S+ b· c S+ b S。

实际上，当一个项不是CCTree项时，如果其组件的首项特征不属于同一属性，则可以从其统一形式推断出该项。因此，提出了拆分规则以生成结构良好的术语。从一个非CCTree项出发。接下来，我们将拆分规则添加到先前的重写系统中，该规则用于当一个项不是CCTree项时，将其转换为CCTree项。

从非CCTree项获得CCTree项的组合重写规则如表2所示。在所提出的重写系统中，[[f(τ)]]表示 f(τ)的语义被替换，但结果被视为一个唯一的项，而不是多个项。此外， τ1: τ2包含两个项 τ1和 τ2，每个都被视为一个新项；而[τ]i指的是 i第τ/∼个组件。与表1相比，仅添加了拆分规则。该规则保证了如果一个项不是CCTree项，如何通过基于上界属性拆分该项来得到一个CCTree项。

规则	条件	动作
(1) (τ ∈ A) | τ → ∅	-	-
(2) (τ = F ∗(τ)) | τ →[[F ∗(τ)]]	-	-
(3) (τ= F ∗(τ)) ∧(W(τ)) ∧(τ∈/ A) | τ →[[Στk∈[τ]1 ∂(τk)]]：…: [[Στk∈[τ]| τ/∼| ∂(τk)]]	-	-
(4) (τ= F ∗(τ)) ∧(∼ W(τ)) | τ →[[split(τ)]]	-	-

为此，首先提供描述接收项τ的属性集A。注意，在分类聚类算法中，属性集是预先已知的。属性集和非CCTree项被输入到组合重写系统中。当规则(τ=F ∗(τ)) ∧(W(τ)) | τ →[[Στk∈[τ]1 ∂(τk)]]: …: [[Στk∈[τ]| τ/∼| ∂(τk)]]对某一项 τ成立时，我们保存 τ。然后将 τ中的所有[[Στk∈[τ]i]]替换为各自符合该规则的后续项。此过程迭代重复，直到所有推导均达到原子项为止。该项的结果即为所求的CCTree项。

示例8 。假设两个CCTree项的加法表示为 τ=a1 S+a2 S+b1 S ′+b2 S ′，其属性集合为 A={a1, a2}， B={b1, b2}。容易验证 τ不是来自表1中规则的CCTree项。我们希望利用组合重写系统，从接收到的非CCTree项 τ中找出一个CCTree项。为此，我们有：

(i)(τ= F ∗(τ))∧(∼ W(τ)) | τ (4) −−→[[split(τ)]]
(ii)[[split(τ)]]= τ′= a1 S+ a2 S+(a1+ a2)· b1 S′+(a1+ a2)· b2 S′
(iii)(τ′ = F ∗ (τ′)) | τ′(2) −−→[[F ∗ (τ′)]]=(a1·(S+b1 S ′)+a2·(S+b1 S ′))= τ′′
(iv)(τ′′= F ∗ (τ′′))∧(W(τ′′)) | τ′′ ∗(3)∗ −−−→ S+ b1 S′(I): S+ b1 S′(II)
(I) S+ b1 S′(4) −−→(b1+ b2)· S+ b1 S′(2) −−→ b1 ·(S+ S′)+ b2 S ∗(3)∗ −−−→ S+ S′: S (1) −−→ ∅: ∅
(II) S+ b1 S′(4) −−→(b1+ b2)· S+ b1 S′(2) −−→ b1 ·(S+ S′)+ b2 · S ∗(3)∗ −−−→ S+ S′: S (1) −−→ ∅: ∅

为了找到生成的CCTree项，我们考虑遵守规则(3)的项，表示为 ∗(3)∗。因此，我们得到它们为：(∗) a1 ·(S+ b1 S′)+ a2 ·(S+b1 S′),(∗∗) b1 ·(S+ S′)+ b2 S,(∗ ∗ ∗) b1 ·(S+ S′)+ b2 · S。然后，由于(∗∗)由该项S+ b1 S′在(∗)内部产生，且(∗ ∗ ∗)由项 S+ b1 S′在(∗)内部产生，我们将其替换为其先前的形式：a1 ·(b1 ·(S+ S′)+ b2 S)+ a2 ·(b1 ·(S+ S′)+ b2 · S)

由于不再有项满足规则(3)，上述项即为所需的CCTree项。可以自动验证所得项是一个CCTree项（表1）。

随后，由两个（或多个）CCTree项组合而成的最终CCTree项将返回至分布式设备，每个智能体的CCTree项需要扩展为最终CCTree项。将每个CCTree项扩展为最终CCTree项的过程将同质化所有CCTree的结构。为此，只需添加一个具有最终CCTree项的CCTree项即可。然后，所有在CCTree项与最终CCTree项组合过程中应用于该CCTree项的 split规则，将显示相关CCTree结构中所需的拆分，遵循[13]中提供的将项转换为树的过程。

3.4 合流的重写系统

在本节中，我们首先介绍重写系统的终止性和合流性的含义。此外，通过若干定理，我们证明了所提出的重写系统具有终止性和合流性。终止性和合流性是重写系统的有趣性质，它们保证：首先，应用所提出系统的重写规则时，不会出现无限循环；并且，我们总能得到唯一结果。

重写系统的终止性与合流性 。 一个重写系统是终止的，如果在 R中不存在无限推导“t1 → t2 → t3 →…”。这意味着每个推导最终都会到达一个范式[3]。兰克福德定理指出，对于某个约简序“>”，若对所有规则“x → y ∈ R”都有“x> y”，则重写系统 R是终止的。一个序称为约简序，当且仅当它是单调的且完全不变的[3]。一个关系是单调的，是指在关系两边添加或约简项时保持序不变；它是完全不变的，是指当关系两边的项被替换时仍保持序不变[3]。在重写系统 R中的元素 t是局部合流的，如果对于所有 x, y ∈ R，满足“t → x”和“t → y”，都存在 u ∈ R使得“x →∗ u”和“y → ∗ u”。如果每一个 t ∈ R都是局部合流的，则称 →为局部合流的。纽曼引理表明，一个终止的重写系统是合流的当且仅当它是局部合流的[3]。

定理2 . CCTree重写系统是终止的。

证明 。 为了证明该定理，我们首先在CCTree重写系统的规则上定义一个约简序。为此，我们定义一个大小函数，该函数接收一个FC‐项并返回该项中出现的特征数量，如下所示：size： FC → N，使得 size(S) = 1, size(f S) = 1, size(F · τ) = |F| +size(τ) size(τ1+ τ2) = size(τ1) + size(τ2)，且我们考虑 size(∅) = 0，以及size(τ1: τ2) = size(τ1)+ size(τ2)。

我们称 FC‐项 τ1小于 FC‐项 τ2，记作 τ1 ≤ τ2，如果 τ1中的特征数量少于 τ2中的特征数量，或者等价地有size(τ1) ≤ size(τ2)。该偏序是良基的，因为不存在无限递降链（特征数量有限）。它是单调的，因为在两个项上同时添加或约简项时，两项中特征数量的关系保持不变。此外，左右两边的替换保持了特征数量的序关系，即它是完全不变的。因此，所提出的序是一种约简序。

考虑到 ∅是不包含任何特征的空项，因此在第一条规则中有 atomic term> ∅。在第二条规则中，仅当项不等于其统一形式时才应用该条件规则；而有序合一函数（如果被应用）不会改变特征的数量，即 τ ≥ F ∗(τ)对应τ = F ∗(τ)，因为 size(τ) = size(F ∗(τ))。值得注意的是，此规则为单步规则，一旦项被统一，则会使用其他规则。在第三条规则中，左侧项的所有组件的第一特征均被移除，即左侧项的大小（特征数量）大于右侧项的大小（特征数量）。因此，所提出的约简序 ≤作用于CCTree重写系统，从而使该系统是终止的。

定理3 。 CCTree重写系统是合流的。

证明 。 在CCTree重写系统中，所有规则都是有条件的，并且不存在同时满足两个（或更多）条件的项。这意味着不可能出现 τ → τ1和 τ → τ2的情况，其中 τ1 = τ2。因此，该重写系统是局部合流的。根据纽曼引理，CCTree重写系统具有终止性（定理2）且局部合流，故其为合流的。

定理4 . 组合重写系统是合流的。

证明 。 与CCTree重写系统相比，组合重写系统新增的唯一规则是规则 split。我们证明该 split规则并不破坏重写系统的终止性和合流性。首先，split规则是一步规则，即 split规则应用一步后所得的结果被视为其他规则（这些规则会减小项）的前提。另一方面，对每一项， split规则的应用次数最多等于属性的数量（有限）。因此，由于 split本身是一步规则，并且对每项仅被调用有限次，故组合重写系统是终止的。

另一方面，不存在同时满足组合重写系统的两个（或多个）条件的项，即不存在项 τ使得 τ →τ 1且 τ → τ 2，其中 τ 1 = τ 2。这意味着该组合重写系统是局部合流的。因此，该组合重写系统是终止的且局部合流的，从而根据纽曼引理，它是合流的。

3.5 集中式与分布式CCTree聚类的复杂度及结果对比

接下来，我们讨论与集中式方法相比，CCTree在分布式设备上进行簇划分的时间复杂度改进。此外，我们指出在何种条件下，分布式模式下生成的CCTree与集式方法得到的CCTree相等。

定理5 。 假设 N为需要聚类的元素总数， k为属性数量， vmax为一个属性中最大取值数量， K为非叶节点的最大数量。在 n分布式设备上构建CCTree的时间复杂度等于 1 n · O(K×(N × m+ N × vmax))。

证明 。在[11],中，构造CCTree的时间复杂度已被计算。再次回顾，设 N为整个数据集中的元素数量，Ni为节点 i中的元素数量， m为特征总数， vl为属性 Al的特征数量， k为属性数量，以及 vmax= max{vl}。在构造CCTree时，若 K= m+ 1表示在完全树中出现的非叶节点的最大数量，则构造包含 N个元素的CCTree所需的最长时间等于O(K×(N × m+ N × vmax))。现在，若将包含 N个点的数据集平均分配到 n个设备上，则创建 n个CCTree所需时间为O(K ×((N/n) × m+(N/n) × vmax)) = 1 n · O(K ×(N × m+ N × vmax))，即总所需时间被除以设备数量。其余部分的代数计算需要常数时间。

定义16（KL散度） 。设 P和 Q是定义在 A1 × A2 ×… × Ak上的两个概率分布，其中 Ai ∈A ∀ ≤ i ≤ k（CCTree聚类中的属性集合）。则从Q到 P的 KL散度[7]，记为 DKL(P||Q)，是通过比较概率分布 Q与概率分布 P得到的一个度量，如下所示：

DKL(P||Q)=∑X i∈ A1×A2×…×Ak p(Xi) log p(Xi) q(Xi)

当且仅当 log p(Xi ) q(Xi)→ ∞ 时，我们将 log p(Xi ) q(Xi) 设为 1。

根据上述定义，对于具有概率分布 P1 和 P2 的两个数据集 D1 和 D2，如果 DKL(P1||P2) 的结果接近于零，则意味着它们具有几乎相同的数据分布。因此，它们将生成相似的CCTree。

定理6 . 设 D1和 D2为两个具有概率分布 P1和 P2（如定义16）的数据集。如果 DKL（P1||P2） = 0，则 CCT ree（D1） =CCT ree（D2）。

证明 。 该证明源于CCTree的结构依赖于每个节点中用于划分数据的属性这一事实。如果两个数据集中的元素分布几乎相等，则意味着相同的属性在这两种情况下，香农熵最高，因此选择该属性的特征标签分支进行数据划分。

定理6指出，如果两个数据集的概率分布相等，则两个智能体得到的CCTree结构也相等。换句话说，当两个概率分布的KL散度趋近于零时，我们分布式框架的结果将与集中式系统的结果更加相似。将该结果推广到多于两个数据集的情况，可表述如下：设有 N数据集 D1, D2,…, Dn，其对应的概率分布分别为 P1, P2,…, Pn。若对所有 DKL(Pi||Pj)= 0成立，则我们分布式框架生成的CCTree等于集中式系统的CCTree。概率分布差异越大（KL散度结果越高），分布式框架最终得到的CCTree与集式方法越有可能不同。在未来的工作中，我们计划通过实际用例实验更详细地验证这一问题。

4 相关工作

在[14]中提出了参与数据挖掘任务的多方之间的知识提取问题。所研究的方法论旨在在各方之间不进行数据披露的情况下执行数据挖掘。该方法论依赖于同态加密和数字信封技术。这些技术的缺点是仅适用于一小部分数据分析函数，并且会带来相当大的开销。在[8],中综述了安全多方计算的基本范式及其与隐私保护数据挖掘的关系。然而，它仅适用于采用所提出计算的数据挖掘算法。Clifton等人[2]提出了一种用于隐私保护分布式数据挖掘中不同应用的工具包。在[10]中提出了用于隐私保护聚类的数据转换方法。在[9],中提出了一种通用框架，以形式化协作系统中隐私保护数据挖掘的架构。然而，据我们所知，本研究是在利用代数结构解决数据挖掘问题方面的最早尝试之一。

5 结论

在当前的研究中，采用了一种名为CCTree的分类聚类算法的抽象表示，以解决隐私保护的分布式聚类问题。通常情况下，为了获得全局效益，分布式代理希望共享其信息以获取自身数据的全局结构。然而，由于隐私顾虑，分布式系统中的代理不愿意公开他们的数据集。为了解决分布式CCTree聚类中的上述挑战，我们提出了一种重写系统，该系统能够自动返回一个CCTree项，使得分布式代理中的所有CCTree能够被同质化。所提出的重写系统的终止性和合流性已被证明，这首先保证了在应用该重写系统时不会出现无限循环，并且最终得到的项是唯一的。

在未来的研究方向中，我们计划将所提出的方法论应用于实际案例研究，以评估其在分布式聚类中的效率。此外，我们计划将所提出的方法推广到更广泛的分布式分类聚类场景中，其中特征在识别簇时起着重要作用，因此适用于抽象。