深度学习笔记：多个视角对L1 L2正则化的理解

1. KKT优化视角：最小化损失函数 + 正则项 ≡ 受不等式约束的最优化（KKT）

设监督学习损失为 $\mathcal{L}(w)$，加上正则项：

• L2 正则化
  $$\underset{w}{\min }\mathcal{L}(w)+\frac{\lambda }{2}\Vert w{\Vert }_2^2$$

• L1 正则化
  $$\underset{w}{\min }\mathcal{L}(w)+\lambda \Vert w{\Vert }_1$$

L2的例子

以平方误差为例，构造拉格朗日函数求梯度：
$$\underset{w}{\min }\frac{1}{2}\Vert y-Xw{\Vert }_2^2\text{s.t.}\Vert w{\Vert }_2^2\le c$$
拉格朗日函数：
$$\mathcal{L}(w,\lambda )=\frac{1}{2}\Vert y-Xw{\Vert }_2^2+\frac{\lambda }{2}(\Vert w{\Vert }_2^2-c),\lambda \ge 0$$
求梯度并令其为 0，整理得：
$$(X^{\top }X+\lambda I)w=X^{\top }y$$

$$\Rightarrow w^{\ast }=(X^{\top }X+\lambda I{)}^{-1}{X}^{\top }y$$

可以发现，L2正则化下权重被均匀缩小，且不会变成 0。

L1的例子

推导过程省略，由于 $\mid w\mid$ 在 0 点不可导，我们使用次梯度形式的KKT条件：

若 $w_i\ne 0$：
$$(X^{\top }(y-Xw){)}_i=\lambda \text{sign}(w_i)$$

• 损失的梯度大小恰好抵消 L1 正则的惩罚力，该特征对优化有足够贡献故保留

若 $w_i=0$：
$$|(X^{\top }(y-Xw){)}_i|\le \lambda$$

• 当某个权重为 0 时，只要损失函数对它的梯度没有超出$\lambda$，就会被锁在 0

因此 L1 会选择特征，让模型更稀疏，贡献小的特征变为0。

---

2. 贝叶斯视角：最大后验估计（MAP）

最小化负MAP：
$$\underset{w}{\min }-\log p(y|X,w)-\log p(w)$$

L2 ≡ 先验高斯分布的MAP

假设权重服从高斯分布，概率密度（取对数，取负数，去常数）：
$$w\sim \mathcal{N}(0,{\sigma }^{2}I)\Rightarrow -\log p(w)\propto \frac{1}{2{\sigma }^2}\Vert w{\Vert }_2^2$$
回代MAP：
$$\underset{w}{\min }-\log p(y|X,w)+\frac{\lambda }{2}\Vert w{\Vert }_2^2$$
其中：
$$\lambda =\frac{1}{{\sigma }^2}$$
发现这就是L2正则化。

同时可以由高斯分布先验的特点推出：

L2正则化，平滑收缩，不稀疏。

L1 ≡ 先验拉普拉斯分布的MAP

假设权重服从拉普拉斯分布，概率密度：
$$w\sim Laplace(0,b)\Rightarrow -\log p(w)\propto \frac{1}{b}\Vert w{\Vert }_1$$
回代MAP：
$$\underset{w}{\min }-\log p(y|X,w)+\lambda \Vert w{\Vert }_1$$
其中：
$$\lambda =\frac{1}{b}$$
发现这就是L1正则化。

同时可以由拉普拉斯分布先验的特点观察出：

峰尖，尾厚，很多权重=0。

可以看图（来自BV1aE411L7sj）：

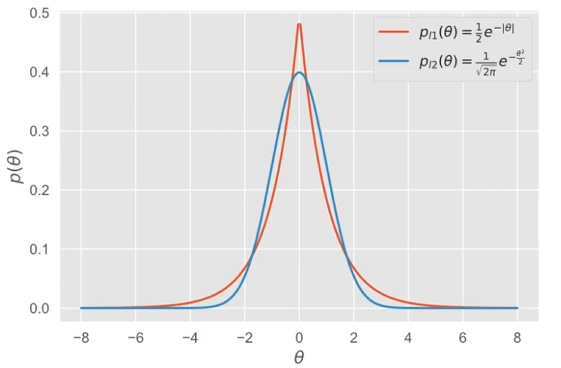
总的来说：

L1和L2正则化就是不同分布先验下的最大后验估计

---

3. 解空间几何视角：可行域形状决定稀疏性

假设最小化 $\mathcal{L}(w)$ 时，等损失线是椭圆。

（图片来自BV1Z44y147xA）

方法	约束形状	结果
L2	球形 $\Vert w{\Vert }_2\le r$	切点平滑 → 非零系数更常见
L1	菱形 $\Vert w{\Vert }_1\le r$	尖角落在坐标轴上 → 易出现 $w_i=0$

---

4. 梯度下降视角：权重衰减(Weight Decay)

SGD+L2 正则化：

SGD更新：
$$w=w-\eta (\nabla \mathcal{L}+\lambda w)=(1-\lambda \eta )w-\eta \nabla \mathcal{L}$$

每步按比例缩，一直都在将权重试图缩小到 0 ，这也是为什么L2正则化（SGD）被叫为权重衰减

注意：非SGD不等价，因为Adam这种自适应优化器会把梯度也缩放，把正则项的梯度破坏了，而SGD是每次按比例衰减，所以必须要解耦，用AdamW

L1 正则梯度（次梯度）：

$$\lambda \cdot \text{sign}(w)$$

不管权重大小，常数地将权重推向 0，很小时也这样，所以作用是稀疏化而不是衰减

---

5. 模型复杂度视角：降低复杂度，防止过拟合

方法	对模型复杂度的影响	特点
L2	连续降低复杂度，对大权重大，小权重小，不挑特征	稳定，平滑，抑制过拟合
L1	直接减少维度（把权重直接变成0）	可解释性高，特征选择，稀疏化

---

6. 实践

场景	推荐
高维 & 要解释性	L1（特征选择）
特征高度相关	L2
深度学习	L2（AdamW）+ 早停

（由chatgpt5辅助整理）