C. Connect Three （曼哈顿距离）_c. connect题解-优快云博客

本文链接：https://blog.youkuaiyun.com/LJD201724114126/article/details/85255391

本文详细解析了一道算法题目“哆啦A梦传送门”，目标是最小化三个点的联通块数量。通过使用曼哈顿距离和中点策略，文章提供了一个有效的解决方案，并附带了完整的C++代码实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题意：给你三个点，让你把它们三个点都联通，有个前提，要使它们的联通块尽可能的少，输出它们。

参考链接：https://www.cnblogs.com/dybala21/p/10171230.html

题解：要想它们两点联通块少，那就必须走曼哈顿距离了，我们假设前两个已经弄好曼哈顿距离了，那么现在我们要加入第三个点，那么我们就尽量让第三条线路连到前两个点组成的线路，这样就会使得联通块尽可能的少了。那么此时有一个转折点，此点就是x，y中点。为什么呢？给你几个图。

上个图：

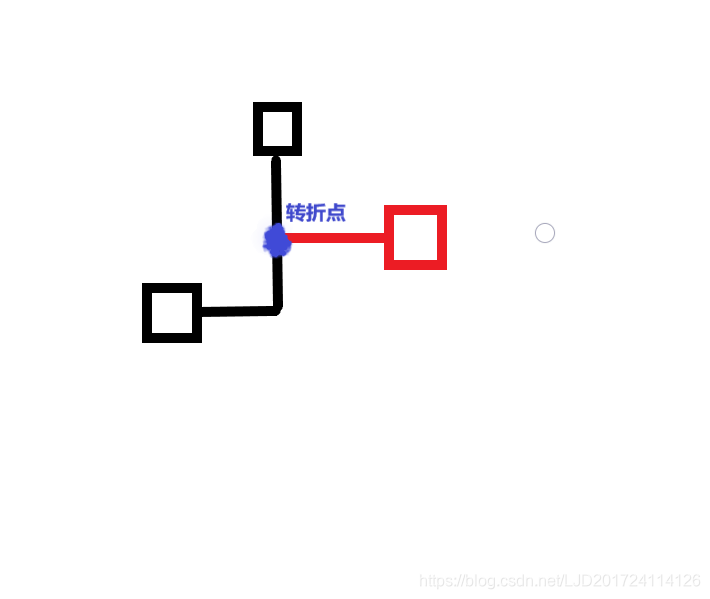
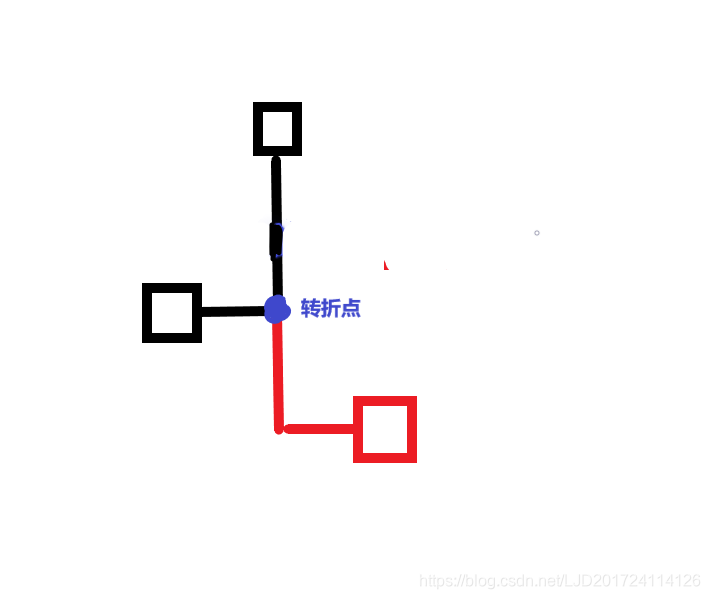
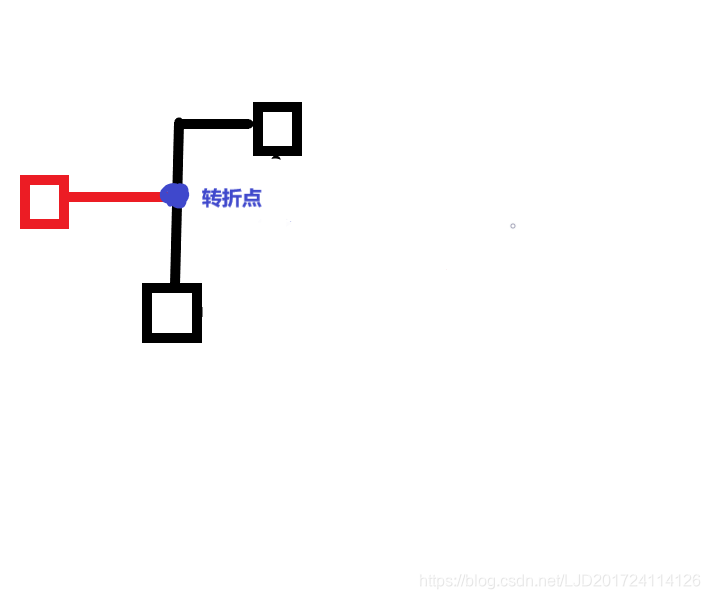
显然转折点都是x，y的中点。

代码所示：

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<set>

using namespace std;

int x[4],y[4];
int xi[4],yi[4];

set<pair<int,int> > point;
set<pair<int,int> > :: iterator iter;

void solve(int a,int b,int ai,int bi)
{
    while(a<ai){
            a++;
        point.insert(make_pair(a,b));
    }
    while(a>ai)
    {
        a--;
        point.insert(make_pair(a,b));
    }
    while(b<bi)
    {
        b++;
        point.insert(make_pair(a,b));
    }
    while(b>bi)
    {
        b--;
        point.insert(make_pair(a,b));
    }
}
int main()
{

    for(int i=0;i<3;i++)
    {
        scanf("%d%d",&x[i],&y[i]);
        xi[i]=x[i];
        yi[i]=y[i];
    }

    sort(xi,xi+3);
    sort(yi,yi+3);

    for(int i=0;i<3;i++)
    {
        point.insert(make_pair(x[i],y[i]));
        solve(x[i],y[i],xi[1],yi[1]);///第i个点与中间点玩曼哈顿距离
    }

    printf("%d\n",point.size());
    for(iter=point.begin();iter!=point.end();iter++)
    {
        printf("%d %d\n",(*iter).first,(*iter).second);
    }


    return 0;
}