牛客网暑期ACM多校训练营(第六场) C （简单排列组合+逆元）

Generation I

链接：https://www.nowcoder.com/acm/contest/144/C
来源：牛客网
 

时间限制：C/C++ 3秒，其他语言6秒
空间限制：C/C++ 262144K，其他语言524288K
64bit IO Format: %lld

题目描述

Oak is given N empty and non-repeatable sets which are numbered from 1 to N.

Now Oak is going to do N operations. In the i-th operation, he will insert an integer x between 1 and M to every set indexed between i and N.

Oak wonders how many different results he can make after the N operations. Two results are different if and only if there exists a set in one result different from the set with the same index in another result.

Please help Oak calculate the answer. As the answer can be extremely large, output it modulo 998244353.

输入描述:

The input starts with one line containing exactly one integer T which is the number of test cases. (1 ≤ T ≤ 20)

Each test case contains one line with two integers N and M indicating the number of sets and the range of integers. (1 ≤ N ≤ 1018, 1 ≤ M ≤ 1018, )

输出描述:

For each test case, output "Case #x: y" in one line (without quotes), where x is the test case number (starting from 1) and y is the number of different results modulo 998244353.

 

示例1

输入

复制

2
2 2
3 4

输出

复制

Case #1: 4
Case #2: 52

 

题意：给定n个集合， 要求用n次操作， 第i次操作用1~m中一个数填入 i ~ n个集合中， 集合无序而且元素不重复。

 

题解：参考这里的：http://www.cnblogs.com/Jadon97/p/9434242.html

https://www.nowcoder.com/discuss/90684?type=101

因为依次填入到1-n集合，很容易想到我们只需考虑最后一个集合就行，例如：

我们以n=4,m=4为例，先举一个4,4的两个集合


我们现在只看第n层，两个不同的集合的最后一层的元素都含有1,2,3，但是这两个集合是不同的两个集合，原因是数字出现的顺序会影响上一层的集合，所以最后一层元素的顺序是影响总的个数的，

 

还有就是填入集合的数只有第一次才是有效的，假设有K个数出现，那么我们可以枚举这k个数，即这k个数的全排列为 。

因为第一个数是不会有影响的， 所以可以把k个数的第一个放到第一位。

剩下的（k-1）个数要放进（n-1）个格子中有种方法， 其实这些位置就是这个数第一次出现的位置， 剩余n-k的位置其实是没有贡献的。

答案就是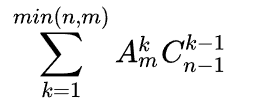

拆开看第k项就是

 

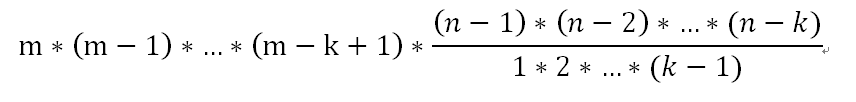
所以可以k从1开始递推：

代码如下：

#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;

const long long MOD = 998244353;
const int maxN = 1e6+10;
typedef long long LL;

LL inv(LL a, LL b){
    LL sum = 1;
    while(b){
        if(b & 1) sum = sum * a % MOD;
        b /= 2;
        a = a * a % MOD;
    }
    return sum;
}
LL n, m, Min;
LL Inv[maxN];
void init() {
    Inv[1] = 1;
//    LL _ = 1;
    for(int i = 2; i <= maxN; i++){
        Inv[i] = inv(i, MOD - 2); ///用费马小定理加快速幂求逆元
    }
}
int main() {
    init();
    int T;
    scanf("%d", &T);
    for(int kase = 1; kase <= T; kase++) {
        scanf("%lld %lld",&n , &m);
        Min = min(n, m);

        m %= MOD, n %= MOD;

        LL ans = m;
        LL sum = m;
        for(int i = 1; i < Min; i++){
            sum = sum * (m - i) % MOD * (n - i) % MOD * Inv[i] % MOD;
            ans += sum;
            ans %= MOD;
        }
        printf("Case #%d: %lld\n",kase,  ans);
    }
}