Connection-based ALOHA 仿真模型
1. 关于Connection-based Aloha的思路(基于连接的Aloha)
摘要
随机接入协议根据数据传输前是否需要建立连接,可分为基于连接 和无连接 两大类。在机器对机器通信中,传统的基于连接机制(如LTE中的授权接入)因连接建立过程带来的开销和延迟而被广泛认为不适用于短数据包传输,导致无连接方案备受青睐。
然而,本研究发现,这种普遍认知存在局限性。通过对基于连接的时隙Aloha 进行精确建模与优化,我们揭示了连接建立的价值所在。我们创新性地提出了一个请求队列模型,以刻画每个节点的队列行为,从而能够精确表征并优化系统的数据吞吐量和数据包的平均排队延迟。
分析表明,连接建立是否有利取决于数据负载与协议开销的权衡。当数据包长度(或批次大小)较大时,连接建立能通过将冲突代价高昂的数据传输转为代价较小的请求冲突,从而显著提升网络性能。我们推导出了连接建立优于无连接方案的关键条件,并将此分析应用于5G网络中的基于授权的4步小数据传输 与无授权的2步小数据传输 方案的性能比较。结果颠覆了传统认知:在当前5G系统参数下,对于典型的M2M场景,基于连接的方案不仅能提供更高的最大吞吐量和更强的鲁棒性,甚至能实现更低的平均排队延迟。
研究意义
这项研究的意义主要体现在理论和实际两个层面:
1. 理论意义
- 建立了新的分析框架:提出的“请求队列模型”解决了长期以来缺乏对基于连接随机接入进行准确节点级建模的挑战,为分析此类协议的队列延迟和稳定性奠定了基础。
- 揭示了性能权衡的本质:研究明确了连接建立与无连接接入之间的根本权衡——即用固定的信令开销来换取冲突代价的降低。通过严格的数学推导,给出了决定优劣的临界条件(如数据包长度阈值),为协议设计提供了清晰的理论指导。
- 统一了性能评估维度:不仅分析了饱和状态下的最大吞吐量,还深入研究了非饱和状态下的延迟性能,提供了更全面、更贴近实际网络运行状态的理论工具。
2. 实际意义
- 修正了对连接建立的偏见:研究结果表明,对于M2M通信,不应一概而论地认为“无连接一定优于基于连接”。它为网络运营商和标准制定者在协议选择上提供了更精细、更科学的决策依据。
- 直接指导5G/6G接入设计:通过对5G NR中RA-SDT方案的案例研究,直接证明了基于连接的4步方案在多数M2M场景下的潜在优势。这为未来5G-Advanced和6G网络中随机接入技术的优化与演进指明了方向,提示我们应重新审视并优化基于连接的机制,而非简单地弃用。
- 提供了实用的优化方法:研究给出了最优传输概率的显式表达式,该表达式仅依赖于长期的统计信息(如总数据输入速率),易于在实际网络中实施,为实现高效的分布式网络控制提供了可行方案。
总结而言,这项工作不仅深化了我们对随机接入机制的理解,更重要的是,它挑战了领域内关于连接建立开销的固有认知,为未来大规模物联网接入网络的高效设计提供了全新的视角和坚实的理论基础。
2. 论文模型思路与数学公式
系统参数
- N: 节点数量
- M: 批次大小(每个批次包含的数据包数)
- λ: 数据包到达率(每个时隙每个节点)
- q: 请求发送概率
- δ: 开销时隙数
- T: 总仿真时隙数
数据包到达过程
每个时隙中,每个节点i的数据包到达服从伯努利过程:
A i ( t ) { 1 , if 以概率 λ 0 , if 以概率 1 − λ A_i(t) \begin{cases} 1, & \text{if 以概率 } \lambda \\ 0, & \text{if 以概率 } 1-\lambda \end{cases} Ai(t){1,0,if 以概率 λif 以概率 1−λ
其中A_i(t)表示节点i在时隙t是否有数据包到达。
批次形成
当节点i的缓冲区中数据包数量达到M时,形成一个批次:
B i ( t ) { 1 , if Q i ( t ) ≥ M 0 , otherwise B_i(t) \begin{cases} 1, & \text{if } Q_i(t) \geq M \\ 0, & \text{otherwise} \end{cases} Bi(t){1,0,if Qi(t)≥Motherwise
其中Q_i(t)为节点i在时隙t的队列长度。
请求发送决策
节点i在时隙t发送请求的条件:
解释:如果形成了的数据包数量>=M,并且传输队列C(t)为空,并且发送了请求,那么认为就可以传输了
R i ( t ) { 1 , if B i ( t ) = 1 and C ( t ) = idle and U ≤ q 0 , otherwise R_i(t) \begin{cases} 1, & \text{if } B_i(t) = 1 \text{ and } C(t) = \text{idle} \text{ and } U \leq q \\ 0, & \text{otherwise} \end{cases} Ri(t){1,0,if Bi(t)=1 and C(t)=idle and U≤qotherwise
其中:
- C(t): 信道状态(idle/busy)
- U ~ Uniform(0,1)
冲突检测
请求发送结果:
Result ( t ) { success , if ∑ i = 1 N R i ( t ) = 1 collision , if ∑ i = 1 N R i ( t ) > 1 idle , if ∑ i = 1 N R i ( t ) = 0 \text{Result}(t) \begin{cases} \text{success}, & \text{if } \sum_{i=1}^{N} R_i(t) = 1 \\ \text{collision}, & \text{if } \sum_{i=1}^{N} R_i(t) > 1 \\ \text{idle}, & \text{if } \sum_{i=1}^{N} R_i(t) = 0 \end{cases} Result(t)⎩ ⎨ ⎧success,collision,idle,if ∑i=1NRi(t)=1if ∑i=1NRi(t)>1if ∑i=1NRi(t)=0
数据传输
请求成功后,节点开始数据传输:
- 传输持续时间:M + δ 个时隙
- 传输数据包数:M 个
- 信道在此期间被占用
吞吐量计算
系统吞吐量定义为成功传输的数据包数与总时隙数的比值:
λ ^ o u t = 总成功传输的数据包数 T \hat{\lambda}_{out} = \frac{\text{总成功传输的数据包数}}{T} λ^out=T总成功传输的数据包数
令S(t)表示时隙t成功传输的数据包数:
S ( t ) { M , if 时隙t开始一次成功传输 0 , otherwise S(t) \begin{cases} M, & \text{if 时隙t开始一次成功传输} \\ 0, & \text{otherwise} \end{cases} S(t){M,0,if 时隙t开始一次成功传输otherwise
则吞吐量为:
λ ^ o u t = 1 T ∑ t = 1 T S ( t ) \hat{\lambda}_{out} = \frac{1}{T} \sum_{t=1}^{T} S(t) λ^out=T1t=1∑TS(t)
仿真流程概述
- 初始化:设置系统参数和各节点状态
- 时隙循环:对每个时隙执行以下操作
- 数据包到达:根据伯努利过程生成新数据包
- 批次检查:检查各节点缓冲区是否达到批次大小M
- 请求处理:在信道空闲时,有批次的节点以概率q发送请求
- 冲突处理:检测请求冲突,处理成功请求
- 数据传输:成功请求的节点占用信道M + δ个时隙进行传输
- 统计计算:记录成功传输的数据包数,计算最终吞吐量
3.主要代码、结果与分析
Main12:
%% 基于连接的时隙Aloha吞吐量仿真 - 修正版本
clear; clc; close all;
%% 仿真参数设置
n = 20;
lambda_val = 0.5; % 到达率
M_values = [1, 2, 4, 8]; % 批大小
delta = 2; % 开销
total_slots = 1e5;
initial_packets = 10; % 初始包数
% q值范围
q_values = [0.001, 0.002, 0.005, 0.008, 0.01, 0.015, 0.02, 0.03, 0.05, 0.08, 0.1];
fprintf('开始仿真...\n');
tic;
%% 预分配和初始化
throughput_results = zeros(length(M_values), length(q_values));
p_success_results = zeros(length(M_values), length(q_values));
%% 主仿真循环
for m_idx = 1:length(M_values)
M = M_values(m_idx);
fprintf('M=%d: ', M);
for q_idx = 1:length(q_values)
q = q_values(q_idx);
% 仿真
[throughput, p_success] = corrected_simulation(n, lambda_val, M, delta, q, total_slots, initial_packets);
throughput_results(m_idx, q_idx) = throughput;
p_success_results(m_idx, q_idx) = p_success;
fprintf('.');
end
fprintf('\n');
end
simulation_time = toc;
fprintf('仿真完成! 总耗时: %.1f 分钟\n', simulation_time/60);
%% 分开绘制两个图
plot_separate_figures(q_values, M_values, throughput_results, p_success_results, n, lambda_val, delta, total_slots);
%% 修正的仿真函数 - 基于讨论的思路
function [throughput, p_success] = corrected_simulation(n, lambda, M, delta, q, total_slots, initial_packets)
% 初始化
data_buffers = ones(n, 1) * initial_packets; % 每个节点的数据包缓冲区
request_queues = zeros(n, 1); % 每个节点的请求队列(批次数量)
% 信道状态
channel_busy = false;
busy_until = 0;
% 计数器
success_packets = 0;
total_requests_sent = 0;
successful_requests = 0;
% 主循环
for current_slot = 1:total_slots
% 1. 数据包到达
for i = 1:n
if rand() < lambda
data_buffers(i) = data_buffers(i) + 1;
end
end
% 2. 更新信道状态
if channel_busy && current_slot >= busy_until
channel_busy = false;
end
% 3. 批次形成
for i = 1:n
% 如果数据包数足够形成新批次,则生成请求
if data_buffers(i) >= M
request_queues(i) = request_queues(i) + 1;
data_buffers(i) = data_buffers(i) - M;
end
end
% 4. 请求发送决策(只在信道空闲时)
requesting_nodes = [];
if ~channel_busy
for i = 1:n
% 如果节点有请求且决定发送
if request_queues(i) > 0 && rand() < q
requesting_nodes(end+1) = i;
total_requests_sent = total_requests_sent + 1;
end
end
% 5. 冲突检测
if length(requesting_nodes) == 1
% 请求成功
successful_requests = successful_requests + 1;
node_idx = requesting_nodes(1);
% 开始数据传输
channel_busy = true;
busy_until = current_slot + M + delta;
% 减少请求队列
request_queues(node_idx) = request_queues(node_idx) - 1;
% 记录成功传输的数据包(整个批次)
success_packets = success_packets + M;
end
% 如果 requesting_nodes 为空或多个,则无操作(信道保持空闲)
end
% 如果信道忙,则跳过请求发送
end
% 计算性能指标
throughput = success_packets / total_slots;
if total_requests_sent > 0
p_success = successful_requests / total_requests_sent;
else
p_success = 0;
end
end
%% 分开绘制两个图的函数
function plot_separate_figures(q_values, M_values, throughput_results, p_success_results, n, lambda_val, delta, total_slots)
colors = lines(length(M_values));
% 图1: 吞吐量
figure('Position', [100, 100, 800, 600]);
hold on; grid on;
for m_idx = 1:length(M_values)
plot(q_values, throughput_results(m_idx, :), 'o-', ...
'Color', colors(m_idx,:), 'LineWidth', 2, ...
'MarkerSize', 6, 'DisplayName', sprintf('M=%d', M_values(m_idx)));
end
q_optimal = 1/n;
y_max = max(throughput_results(:)) * 1.1;
plot([q_optimal, q_optimal], [0, y_max], 'k--', 'LineWidth', 2, ...
'DisplayName', sprintf('q*=1/n=%.3f', q_optimal));
xlabel('传输概率 q', 'FontSize', 12);
ylabel('吞吐量 \lambda_{out}', 'FontSize', 12);
title('基于连接的时隙Aloha - 吞吐量性能', 'FontSize', 14);
legend('show', 'Location', 'best', 'FontSize', 10);
set(gca, 'XScale', 'log', 'FontSize', 10);
% 图2: 成功概率
figure('Position', [200, 100, 800, 600]);
hold on; grid on;
for m_idx = 1:length(M_values)
M = M_values(m_idx);
plot(q_values, p_success_results(m_idx, :), 's-', ...
'Color', colors(m_idx,:), 'LineWidth', 2, ...
'MarkerSize', 6, 'DisplayName', sprintf('M=%d 仿真', M));
% 理论值(饱和状态)
p_theory_saturated = exp(-n * q_values);
plot(q_values, p_theory_saturated, '--', 'Color', colors(m_idx,:), ...
'LineWidth', 1, 'DisplayName', sprintf('M=%d 理论(饱和)', M));
end
xlabel('传输概率 q', 'FontSize', 12);
ylabel('成功概率 p', 'FontSize', 12);
title('基于连接的时隙Aloha - 成功概率', 'FontSize', 14);
legend('show', 'Location', 'best', 'FontSize', 10);
set(gca, 'XScale', 'log', 'FontSize', 10);
ylim([0, 1]);
% 输出性能分析
fprintf('\n=== 性能分析 ===\n');
for m_idx = 1:length(M_values)
M = M_values(m_idx);
max_throughput = max(throughput_results(m_idx, :));
optimal_q_idx = find(throughput_results(m_idx, :) == max_throughput, 1);
optimal_q = q_values(optimal_q_idx);
p_at_optimal = p_success_results(m_idx, optimal_q_idx);
fprintf('M=%d: 最大吞吐量 = %.4f (q=%.4f), 此时成功概率 = %.4f\n', ...
M, max_throughput, optimal_q, p_at_optimal);
end
% 计算并显示理论最大吞吐量
fprintf('\n=== 理论最大吞吐量 ===\n');
for M = M_values
lambda_max_theoretical = M / (M + delta + exp(1) - 1);
fprintf('M=%d: 理论最大吞吐量 = %.4f\n', M, lambda_max_theoretical);
end
% 显示仿真参数
fprintf('\n=== 仿真参数 ===\n');
fprintf('节点数 n = %d\n', n);
fprintf('数据包到达率 λ = %.2f\n', lambda_val);
fprintf('开销时隙数 δ = %d\n', delta);
fprintf('总仿真时隙数 = %d\n', total_slots);
end
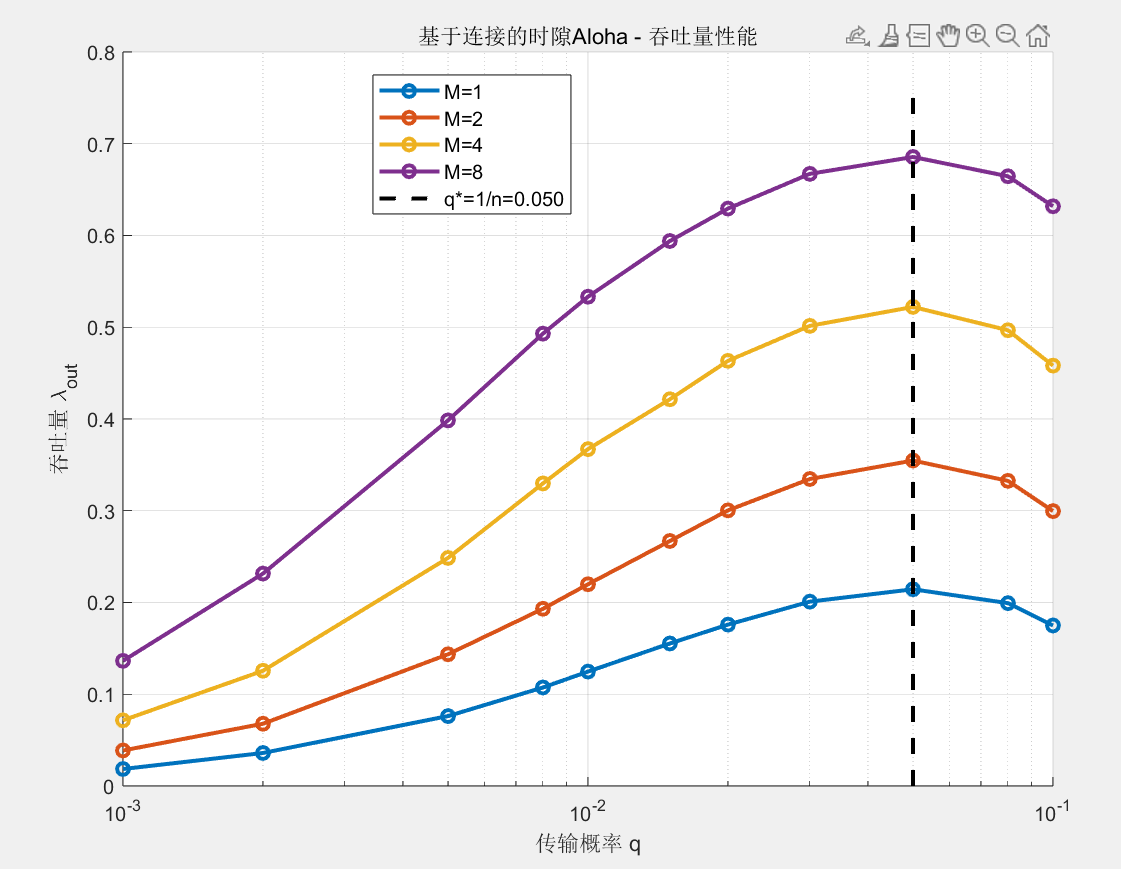
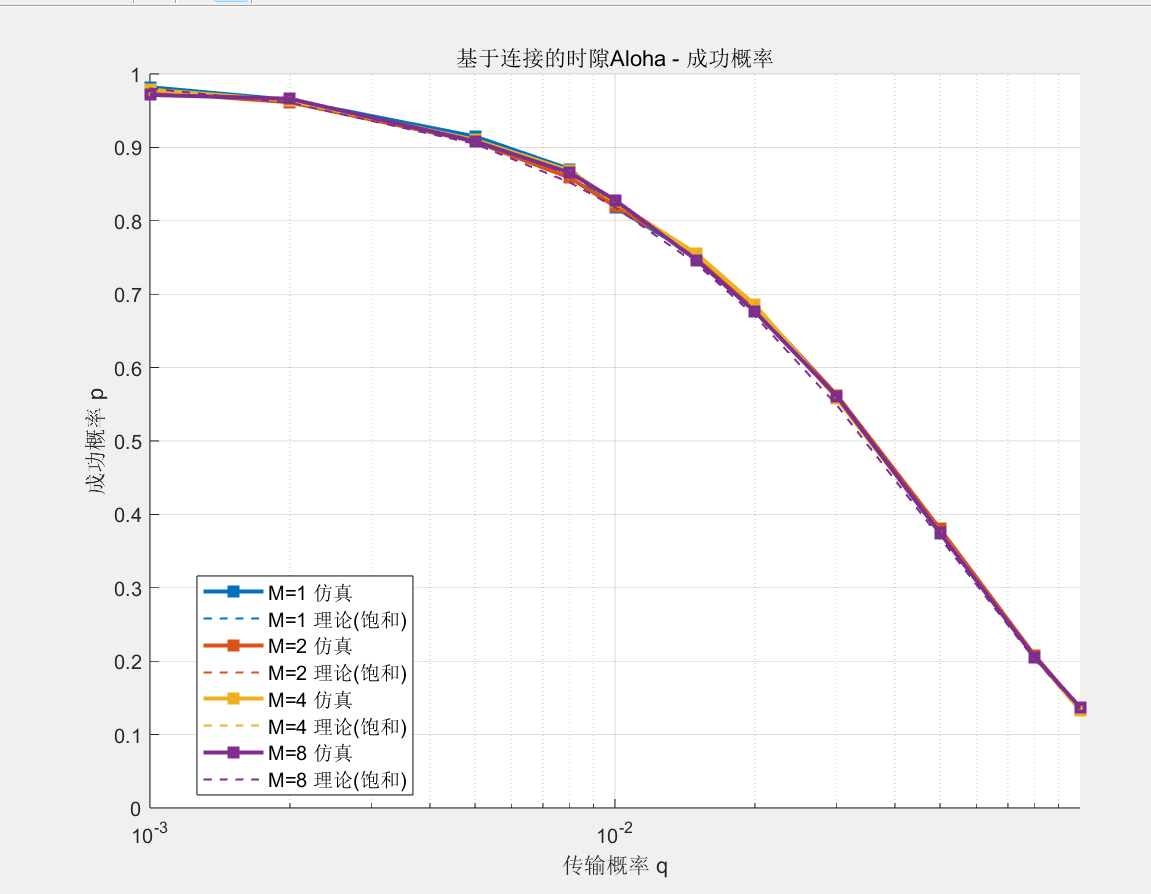
论文的结果:
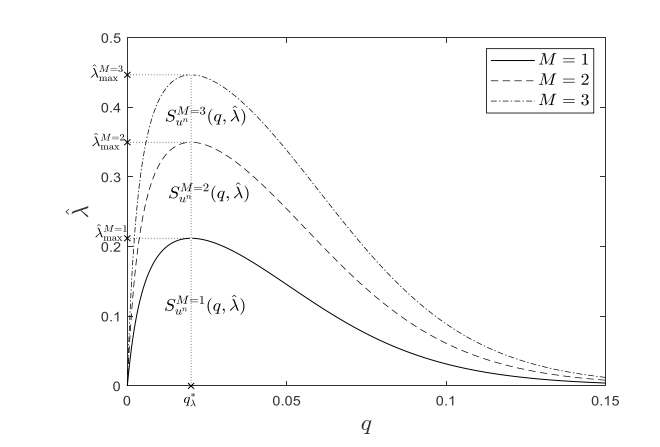
分析:可以看出,成功概率的理论值与仿真值接近,并且吞吐量仿真图像与论文中的图像基本一致,最大值取值点符合理论值。并且λ值与论文中的值也接近,所以认为仿真效果很好
Main7:
clc;clear;close all;
%% 比较三种协议的信令开销(饱和情况下) :仿真 1:GF 3:SAST 5:CBA
ACB_bw_simu=[0.0001,0.001:0.001:0.01];
Lambda_total=1;%总包到达率
Node_num=100;
Total_slot=2e6;
Node_state=zeros(100,2);
% CBA协议参数
M = 4; % 批次大小
delta = 3; % 信令开销时隙数
% 运行三种协议的仿真
[throughputD_simu1,pt_simu1,ST1] = GF_1(Node_state,ACB_bw_simu,Lambda_total,Total_slot);
[throughputD_simu3,throughputA_simu3,pt_simu3,ST3] = SAST_1(Node_state,ACB_bw_simu,Lambda_total,Total_slot);
[throughputD_simu5,ST5] = CBA_corrected(Node_state,ACB_bw_simu,Lambda_total,Total_slot,M,delta);
% 计算信令传输比
STR1_simu=ST1./throughputD_simu1;
STR3_simu=ST3./throughputD_simu3;
STR5_simu=ST5./throughputD_simu5;
%% 理论分析
ACB_bw_ana=linspace(0.0001,0.01,100);
% 原有理论公式
STR1_ana=2*exp(Node_num.*ACB_bw_ana);
nq=Node_num.*ACB_bw_ana;
STR3_ana=2*exp(nq)+2*nq-exp(-nq);
% CBA理论公式
STR5_ana = (exp(nq) ./ ACB_bw_ana + delta - 1) / M;
%% 画图 - 饱和的信令开销(包含CBA理论曲线)
figure
hold on;
% 颜色配置
figcol=cell(1,4);
figcol{1}='#336633'; % GF - 绿色
figcol{2}='#5C0DAC'; % SAST - 紫色
figcol{3}='#FF8C00'; % CBA - 橙色
figcol{4}='#FF0000'; % CBA理论 - 红色
% 标记形状配置
figshape=cell(1,4);
figshape{1}='*';
figshape{2}='O';
figshape{3}='diamond';
figshape{4}='none'; % 理论曲线不需要标记
linewidth=1;
markersize=60;
% GF协议
i=1;
f1=plot(ACB_bw_ana,STR1_ana,'-','color',figcol{i},'LineWidth',linewidth);
s1=scatter(ACB_bw_simu,STR1_simu,markersize,'MarkerEdgeColor',figcol{i},...
'Marker',figshape{i},'LineWidth',linewidth);
% SAST协议
i=2;
f2=plot(ACB_bw_ana,STR3_ana,'--','color',figcol{i},'LineWidth',linewidth);
s2=scatter(ACB_bw_simu,STR3_simu,markersize,'MarkerEdgeColor',figcol{i},...
'Marker',figshape{i},'LineWidth',linewidth);
% CBA协议仿真结果
i=3;
s5=scatter(ACB_bw_simu,STR5_simu,markersize,'MarkerEdgeColor',figcol{i},...
'Marker',figshape{i},'LineWidth',linewidth);
% CBA理论曲线
i=4;
f5_theory=plot(ACB_bw_ana,STR5_ana,'-','color',figcol{i},'LineWidth',linewidth+1);
hold off;
% 设置Y轴为对数坐标,以便同时显示不同数量级的数据
set(gca, 'YScale', 'log');
xlim([0,max(ACB_bw_ana)]);
xlabel('$q$','Interpreter','latex');
ylabel('STR','Interpreter','tex','rotation',0,'Horizontalalignment','right');
legend([f1,s1,f2,s2,s5,f5_theory],{'GF Analysis','GF Simulation','SAST Analysis','SAST Simulation',...
'CBA Simulation','CBA Theory'});
set (gca,'position',[0.15,0.15,0.7,0.7],'LineWidth',0.5,'fontsize',14,'FontName','Times New Roman');
set(gcf,'unit','normalized','position', [.2,.2,0.4,0.45]);
box on
%% 输出调试信息
fprintf('=== 调试信息 ===\n');
fprintf('CBA参数: M=%d, delta=%d\n', M, delta);
fprintf('q值范围: %.4f 到 %.4f\n', min(ACB_bw_simu), max(ACB_bw_simu));
% 计算理论值与仿真值的差异
for i = 1:length(ACB_bw_simu)
q = ACB_bw_simu(i);
nq_val = Node_num * q;
theory_val = (exp(nq_val) / q + delta - 1) / M;
sim_val = STR5_simu(i);
error_percent = abs(theory_val - sim_val) / theory_val * 100;
fprintf('q=%.4f: 理论=%.2f, 仿真=%.2f, 误差=%.1f%%\n', ...
q, theory_val, sim_val, error_percent);
end
% 单独绘制CBA的详细分析图
figure;
hold on;
plot(ACB_bw_ana, STR5_ana, 'r-', 'LineWidth', 2, 'DisplayName', 'CBA Theory');
scatter(ACB_bw_simu, STR5_simu, 100, 'b', 'filled', 'DisplayName', 'CBA Simulation');
set(gca, 'YScale', 'log');
xlabel('$q$','Interpreter','latex');
ylabel('STR','Interpreter','tex','rotation',0,'Horizontalalignment','right');
title('CBA协议详细分析');
legend('show');
grid on;
hold off;
function [throughputD_simu, ST_simu] = CBA_corrected(Node_state, ACB_bw_simu, Lambda_total, Total_slot, M, delta)
n = size(Node_state, 1); % 节点数
q_values = ACB_bw_simu; % 传输概率
lambda = Lambda_total / n; % 每个节点的到达率
throughputD_simu = zeros(size(q_values));
ST_simu = zeros(size(q_values));
for q_idx = 1:length(q_values)
q = q_values(q_idx);
% 初始化
data_buffers = ones(n, 1) * 20; % 初始数据包数
request_queues = zeros(n, 1); % 请求队列(批次数量)
% 信道状态
channel_busy = false;
busy_until = 0;
current_transmission_node = 0; % 当前正在传输的节点
% 计数器
success_packets = 0; % 成功传输的数据包总数
signaling_slots = 0; % 信令时隙总数
success_transmissions = 0; % 成功传输次数
% 主循环
for current_slot = 1:Total_slot
% 1. 数据包到达
for i = 1:n
if rand() < lambda
data_buffers(i) = data_buffers(i) + 1;
end
end
% 2. 更新信道状态
if channel_busy && current_slot >= busy_until
channel_busy = false;
current_transmission_node = 0;
end
% 3. 批次形成
for i = 1:n
% 如果数据包数足够形成新批次,则生成请求
while data_buffers(i) >= M
request_queues(i) = request_queues(i) + 1;
data_buffers(i) = data_buffers(i) - M;
end
end
% 4. 请求发送决策(只在信道空闲时)
requesting_nodes = [];
if ~channel_busy
for i = 1:n
% 如果节点有请求且决定发送
if request_queues(i) > 0 && rand() < q
requesting_nodes(end+1) = i;
end
end
% 5. 冲突检测和信令统计
if ~isempty(requesting_nodes)
% 统计信令时隙(请求时隙)
signaling_slots = signaling_slots + 1;
% 如果恰好一个请求,则成功
if length(requesting_nodes) == 1
node_idx = requesting_nodes(1);
% 开始数据传输
channel_busy = true;
busy_until = current_slot + M + delta - 1; % 修正:包括当前时隙
current_transmission_node = node_idx;
% 减少请求队列
request_queues(node_idx) = request_queues(node_idx) - 1;
% 记录成功传输
success_transmissions = success_transmissions + 1;
success_packets = success_packets + M;
% 统计数据传输期间的信令时隙(额外开销)
signaling_slots = signaling_slots + (delta - 1); % 减去已经统计的请求时隙
end
% 如果多个请求(冲突),只统计了请求时隙,没有额外开销
end
else
% 信道忙时的处理:如果是数据传输期间的信令时隙,需要统计
if channel_busy && current_slot > busy_until - (delta - 1) && current_slot <= busy_until - M
% 这是在数据传输阶段但还在信令开销期间
signaling_slots = signaling_slots + 1;
end
end
% 6. 确保系统饱和(如果数据缓冲区空了,添加数据包)
for i = 1:n
if data_buffers(i) < M && request_queues(i) == 0
% 添加足够的数据包来保持系统饱和
data_buffers(i) = data_buffers(i) + M;
end
end
end
% 计算性能指标
throughputD_simu(q_idx) = success_packets / Total_slot;
if success_transmissions > 0
% ST = 总信令时隙数 / 成功传输次数
ST_simu(q_idx) = signaling_slots / success_transmissions;
else
ST_simu(q_idx) = 0;
end
% 调试输出
fprintf('q=%.4f: 吞吐量=%.4f, ST=%.2f, 成功传输=%d, 信令时隙=%d\n', ...
q, throughputD_simu(q_idx), ST_simu(q_idx), success_transmissions, signaling_slots);
end
end
STR结果:
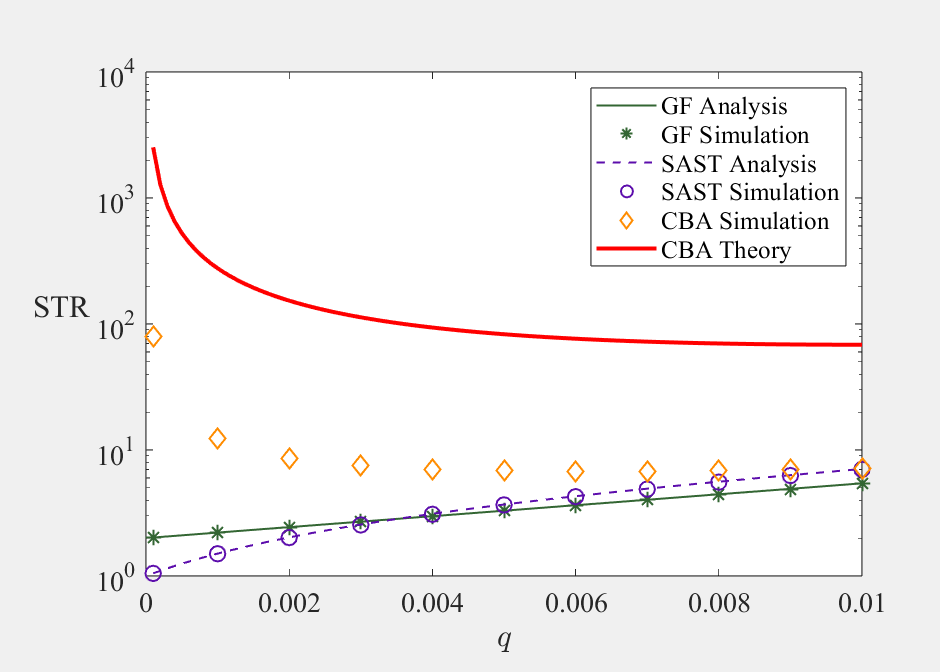
主体仿真思路与前面吞吐量完全相同
分析:与标准协议Slotted Aloha对比后,发现STR值比较接近,但大于SAST和SA,所以可以认为仿真效果较好,但STR指标不能说明CBA比SAST和SA好。对于理论的值分析情况则过于理想,且采取的量纲并不相同,差别有点大,但可以看出变化趋势接近。
4.补充的两个指标
公平性检验:
思路:
这段代码的主要思路是通过仿真评估Connection-based Aloha协议在饱和情况下的公平性性能。以下是详细分析:
主要思路
1. 仿真场景设置
- 饱和条件:每个节点初始都有M个数据包,始终保持有数据待传输(这样能保证每一刻每一点都能参与竞争,在不饱和条件下每个点数据包个数并不相同,不好比较。为了简化我们直接讨论饱和情况)
- 协议行为:模拟CBA协议的核心机制 - 先请求后传输
- 公平性指标:使用Jain公平性指数量化节点间的吞吐量分布
2. 关键状态变量
node_data % 每个节点的数据包数量(保持饱和)
node_connected % 节点是否已建立连接(正在传输)
node_remaining % 剩余传输时隙数
node_data_transmitted % 当前传输中已发送的数据包数
node_success_count % 各节点成功传输的总数据包数
3. 协议执行流程
每个时隙的步骤:
-
请求阶段:
- 检查未连接且有数据的节点
- 每个合格节点以概率q发送请求
- 如果恰好只有一个节点发送请求,则请求成功
-
连接建立:
- 成功节点进入连接状态
- 设置总传输时间:
M + delta - 1个时隙 - 重置当前传输计数器
-
数据传输阶段:
- 所有已连接节点减少剩余时间
- 关键逻辑:只有在数据传输阶段(后M个时隙)才实际传输数据
- 每个数据传输时隙发送1个数据包
- 更新成功计数器
-
传输完成:
- 剩余时间为0时断开连接
- 立即补充数据包到M个(维持饱和)
4. 公平性计算
% Jain公平性指数公式
fairness = (sum_throughput^2) / (Node_num * sum_squared_throughput)
Jain指数的意义:
- 值域:[0, 1]
- 1表示完全公平(所有节点吞吐量相同)
- 0表示完全不公平(只有一个节点获得服务)
5. 仿真特点
饱和条件保证:
- 初始状态:每个节点都有M个数据包
- 传输完成后立即补充到M个
- 确保系统始终处于饱和状态,公平性评估更有意义
协议准确性:
- 区分信令阶段和数据传输阶段
- 正确模拟"只有一个请求成功"的冲突检测
- 精确跟踪每个节点的传输状态
6. 应用价值
这个公平性仿真可以用于:
- 比较不同传输概率q对公平性的影响
- 评估批次大小M和信令开销delta对公平性的影响
- 为协议参数优化提供依据,在吞吐量和公平性之间权衡
总结:该代码通过精确模拟CBA协议在饱和条件下的运行,统计各节点的吞吐量分布,使用Jain指数量化公平性,为协议性能评估提供了重要指标。
function [fairness, node_throughputs] = CBA_fairness(q, Lambda_total, Node_num, Total_slot, M, delta)
% CBA协议公平性仿真函数
% 输入参数:
% q - 传输概率
% Lambda_total - 总到达率
% Node_num - 节点数量
% Total_slot - 总时隙数
% M - 批次大小
% delta - 信令开销时隙数
% 输出:
% fairness - Jain公平性指数
% node_throughputs - 各节点的吞吐量
% 初始化节点状态
node_data = ones(Node_num, 1) * M; % 饱和情况,每个节点有M个包
node_connected = false(Node_num, 1);
node_remaining = zeros(Node_num, 1);
node_data_transmitted = zeros(Node_num, 1); % 当前传输中已发送的数据包数
% 记录每个节点的成功传输数据包数
node_success_count = zeros(Node_num, 1);
for slot = 1:Total_slot
% 请求阶段
can_request = ~node_connected & (node_data >= 1); % 只要有数据包就可以请求
requesting_nodes = find(can_request & (rand(Node_num, 1) < q));
% 检查请求成功(只有一个节点发送)
if length(requesting_nodes) == 1
node_id = requesting_nodes(1);
node_connected(node_id) = true;
node_remaining(node_id) = M + delta - 1; % 总传输时间
node_data_transmitted(node_id) = 0; % 重置已传输数据包计数
end
% 数据传输阶段
transmitting = find(node_connected);
for i = 1:length(transmitting)
node_id = transmitting(i);
node_remaining(node_id) = node_remaining(node_id) - 1;
% 检查是否在数据传输阶段(跳过信令阶段)
if node_remaining(node_id) < M % 后M个时隙是数据传输
% 每个数据传输时隙发送1个数据包
if node_data(node_id) >= 1 && node_data_transmitted(node_id) < M
node_success_count(node_id) = node_success_count(node_id) + 1;
node_data(node_id) = node_data(node_id) - 1;
node_data_transmitted(node_id) = node_data_transmitted(node_id) + 1;
end
end
% 检查传输是否完成
if node_remaining(node_id) == 0
node_connected(node_id) = false;
% 饱和情况:补充数据包到M个
node_data(node_id) = M;
end
end
end
% 计算各节点的吞吐量(数据包/时隙)
node_throughputs = node_success_count / Total_slot;
% 计算Jain公平性指数
sum_throughput = sum(node_throughputs);
sum_squared_throughput = sum(node_throughputs.^2);
if sum_squared_throughput > 0
fairness = (sum_throughput^2) / (Node_num * sum_squared_throughput);
else
fairness = 0;
end
% 调试信息
fprintf(' CBA公平性: %.4f (吞吐量范围: %.6f - %.6f)\n', ...
fairness, min(node_throughputs), max(node_throughputs));
end
Main9:
clc;clear;close all;
%% 公平性仿真比较:GF vs SAST vs 时隙ALOHA vs CBA
% 减少q值的数量
ACB_bw_simu = [0.0001, 0.001, 0.005, 0.01, 0.015, 0.02];
Lambda_total = 1; % 饱和情况
Node_num = 100;
Total_slot = 5e5; % 减少总时隙数
% CBA协议参数
M = 4; % 批次大小
delta = 3; % 信令开销时隙数
% 根据操作系统选择合适的中文字体
if ismac
% macOS 系统
font_name = 'PingFang SC';
elseif isunix
% Linux 系统
font_name = 'WenQuanYi Micro Hei';
elseif ispc
% Windows 系统
font_name = 'Microsoft YaHei';
else
font_name = 'SimHei';
end
% 运行四种协议的公平性仿真
fairness1_simu = zeros(size(ACB_bw_simu));
fairness3_simu = zeros(size(ACB_bw_simu));
fairness4_simu = zeros(size(ACB_bw_simu));
fairness5_simu = zeros(size(ACB_bw_simu)); % CBA协议
% 使用普通for循环(如果可用,可以考虑使用parfor)
% 如果有并行工具箱,可以取消注释下面的parfor,并注释掉for循环
% parfor k = 1:length(ACB_bw_simu)
for k = 1:length(ACB_bw_simu)
q = ACB_bw_simu(k);
fprintf('正在进行公平性仿真: q=%.4f (%d/%d)\n', q, k, length(ACB_bw_simu));
% GF协议公平性仿真
[fairness1_simu(k), ~] = GF_fairness(q, Lambda_total, Node_num, Total_slot);
% SAST协议公平性仿真
[fairness3_simu(k), ~] = SAST_fairness(q, Lambda_total, Node_num, Total_slot);
% 时隙ALOHA公平性仿真
[fairness4_simu(k), ~] = ALOHA_fairness(q, Lambda_total, Node_num, Total_slot);
% CBA协议公平性仿真
[fairness5_simu(k), ~] = CBA_fairness(q, Lambda_total, Node_num, Total_slot, M, delta);
end
%% 画图 - 公平性比较
figure
hold on;
% 颜色配置
figcol = cell(1,4);
figcol{1} = '#336633'; % GF - 绿色
figcol{2} = '#5C0DAC'; % SAST - 紫色
figcol{3} = '#FF0000'; % 时隙ALOHA - 红色
figcol{4} = '#FF8C00'; % CBA - 橙色
% 标记形状配置
figshape = cell(1,4);
figshape{1} = '*';
figshape{2} = 'O';
figshape{3} = 'square';
figshape{4} = 'diamond';
linewidth = 2;
markersize = 80;
% 绘制公平性曲线
plot(ACB_bw_simu, fairness1_simu, '-', 'color', figcol{1}, 'LineWidth', linewidth);
scatter(ACB_bw_simu, fairness1_simu, markersize, 'MarkerEdgeColor', figcol{1}, ...
'Marker', figshape{1}, 'LineWidth', linewidth);
plot(ACB_bw_simu, fairness3_simu, '--', 'color', figcol{2}, 'LineWidth', linewidth);
scatter(ACB_bw_simu, fairness3_simu, markersize, 'MarkerEdgeColor', figcol{2}, ...
'Marker', figshape{2}, 'LineWidth', linewidth);
plot(ACB_bw_simu, fairness4_simu, ':', 'color', figcol{3}, 'LineWidth', linewidth);
scatter(ACB_bw_simu, fairness4_simu, markersize, 'MarkerEdgeColor', figcol{3}, ...
'Marker', figshape{3}, 'LineWidth', linewidth);
plot(ACB_bw_simu, fairness5_simu, '-.', 'color', figcol{4}, 'LineWidth', linewidth);
scatter(ACB_bw_simu, fairness5_simu, markersize, 'MarkerEdgeColor', figcol{4}, ...
'Marker', figshape{4}, 'LineWidth', linewidth);
hold off;
xlim([0, max(ACB_bw_simu)]);
ylim([0, 1]);
% 使用替代方案设置字体
xlabel('传输概率 q', 'FontSize', 12, 'FontName', font_name);
ylabel('Jain公平性指数', 'FontSize', 12, 'FontName', font_name, ...
'rotation', 0, 'Horizontalalignment', 'right');
title('四种协议的公平性比较', 'FontSize', 14, 'FontName', font_name);
legend('GF协议', 'SAST协议', '时隙ALOHA', 'CBA协议', 'Location', 'best', ...
'FontName', font_name, 'FontSize', 10);
% 统一设置坐标轴字体
set(gca, 'position', [0.15, 0.15, 0.7, 0.7], 'LineWidth', 0.5, ...
'fontsize', 12, 'FontName', font_name);
set(gcf, 'unit', 'normalized', 'position', [.2, .2, 0.4, 0.45]);
grid on;
box on;
% 显示当前使用的字体
fprintf('当前使用字体: %s\n', font_name);
save('fairness_comparison.mat');
%% 输出公平性分析结果
fprintf('\n=== 公平性分析结果 ===\n');
fprintf('协议\t\t平均公平性指数\t最小公平性指数\n');
fprintf('GF\t\t%.4f\t\t%.4f\n', mean(fairness1_simu), min(fairness1_simu));
fprintf('SAST\t\t%.4f\t\t%.4f\n', mean(fairness3_simu), min(fairness3_simu));
fprintf('时隙ALOHA\t%.4f\t\t%.4f\n', mean(fairness4_simu), min(fairness4_simu));
fprintf('CBA\t\t%.4f\t\t%.4f\n', mean(fairness5_simu), min(fairness5_simu));
结果: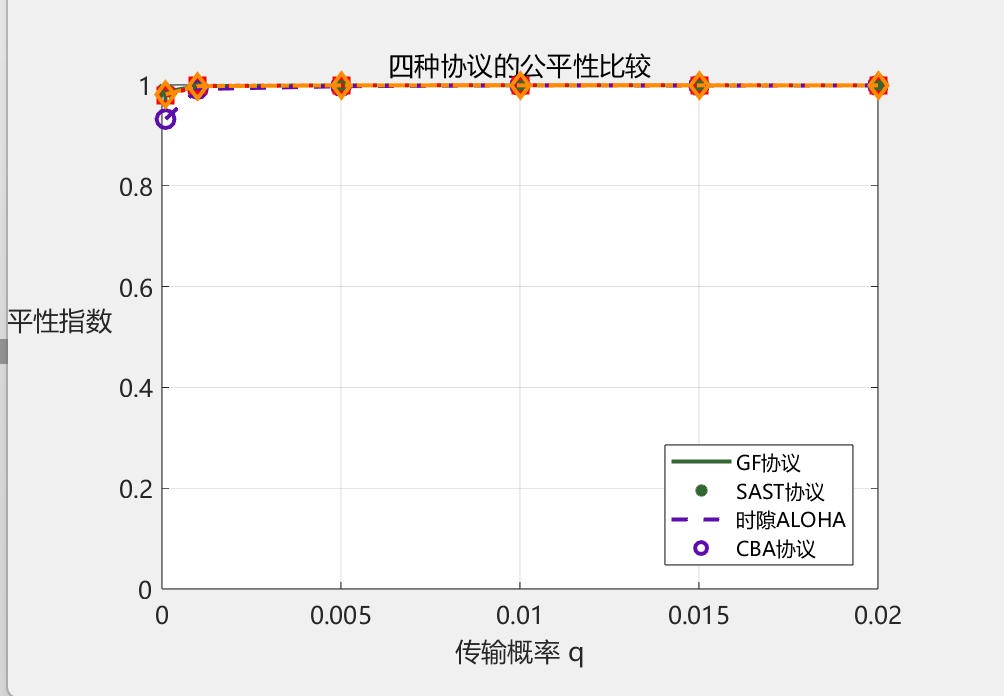
分析:可以看出公平性指标接近于1,δ和q值大小确实不影响公平性指数,符合理论分析。不过还可以进一步探讨不同q值,不同M值对协议的公平性指标影响。这里不做分析了
用不饱和情况尝试一下(方便以后调参数q,M,δ测试)
function [fairness, node_throughputs, avg_throughput] = CBA_fairness_corrected(q, Lambda_total, Node_num, Total_slot, M, delta)
% CBA协议公平性仿真函数 - 严格按照指定步骤
% 1.模拟数据包达到 2.批次形成(数据包数量>=M) 3.请求发送决策 4.冲突检测
% 5.传输状态更新,如果传输队列里还有数据,则认为本时隙传输这个数据
% 初始化节点状态 - 非饱和情况
node_data = zeros(Node_num, 1); % 每个节点的数据包数量
transmission_queue = zeros(Node_num, 1); % 传输队列中剩余的数据包数
node_connected = false(Node_num, 1); % 节点是否已建立连接
node_success_count = zeros(Node_num, 1); % 各节点成功传输的总数据包数
% 每个节点的数据包到达率
lambda_per_node = Lambda_total / Node_num;
% 记录每个节点的传输次数
node_transmission_count = zeros(Node_num, 1);
% 主仿真循环
for slot = 1:Total_slot
% 步骤1: 模拟数据包到达
for i = 1:Node_num
if rand() < lambda_per_node
node_data(i) = node_data(i) + 1;
end
end
% 步骤2: 批次形成(数据包数量>=M)
% 步骤3: 请求发送决策
requesting_nodes = [];
for i = 1:Node_num
% 检查是否有足够数据包形成批次且未在传输中
if node_data(i) >= M && ~node_connected(i)
if rand() < q
requesting_nodes(end+1) = i;
end
end
end
% 步骤4: 冲突检测
% 如果同一时间有多个请求,则发生冲突
% 只有一个请求时才将这个节点的一个批次共M个数据加入传输队列
if length(requesting_nodes) == 1
node_id = requesting_nodes(1);
% 建立连接,将M个数据包加入传输队列
node_connected(node_id) = true;
transmission_queue(node_id) = M;
node_data(node_id) = node_data(node_id) - M; % 从数据包中扣除
% 记录传输次数
node_transmission_count(node_id) = node_transmission_count(node_id) + 1;
end
% 步骤5: 传输状态更新
for i = 1:Node_num
if node_connected(i) && transmission_queue(i) > 0
% 传输一个数据包
node_success_count(i) = node_success_count(i) + 1;
transmission_queue(i) = transmission_queue(i) - 1;
% 如果传输队列为空,断开连接
if transmission_queue(i) == 0
node_connected(i) = false;
end
end
end
end
% 计算各节点的吞吐量(数据包/时隙)
node_throughputs = node_success_count / Total_slot;
avg_throughput = sum(node_success_count) / Total_slot;
% 计算Jain公平性指数
sum_throughput = sum(node_throughputs);
sum_squared_throughput = sum(node_throughputs.^2);
if sum_squared_throughput > 0
fairness = (sum_throughput^2) / (Node_num * sum_squared_throughput);
else
fairness = 0;
end
% 调试信息
fprintf(' CBA公平性分析 (按指定步骤):\n');
fprintf(' Jain公平性指数: %.4f\n', fairness);
fprintf(' 网络平均吞吐量: %.6f\n', avg_throughput);
fprintf(' 节点吞吐量范围: %.6f - %.6f\n', min(node_throughputs), max(node_throughputs));
fprintf(' 节点传输次数范围: %d - %d\n', min(node_transmission_count), max(node_transmission_count));
active_nodes = sum(node_throughputs > 0);
fprintf(' 活跃节点比例: %.1f%% (%d/%d)\n', active_nodes/Node_num*100, active_nodes, Node_num);
end
结果:
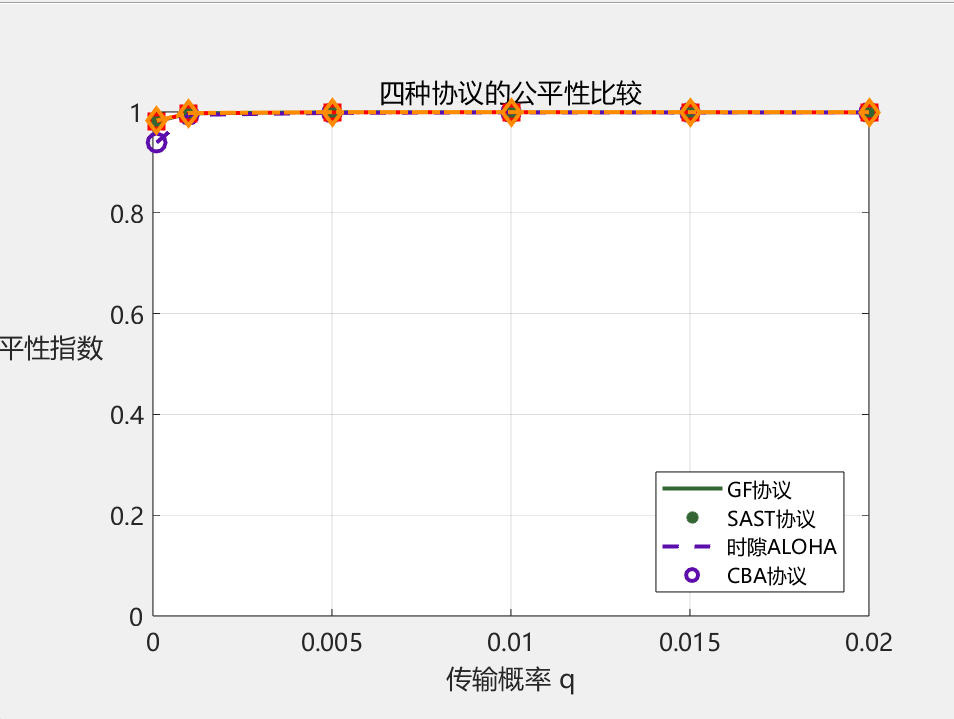
分析:不饱和结果与饱和结果相近
时延性
CBA协议时延仿真代码的完整思路
总体目标
设计一个Connection-based Aloha(CBA)协议的时延仿真函数,用于分析数据包从到达系统到成功传输的时延特性。
核心设计思路
1. 协议行为模拟
按照CBA协议的五个关键步骤进行仿真:
- 数据包到达 → 2. 批次形成 → 3. 请求发送决策 → 4. 冲突检测 → 5. 传输状态更新
2. 节点状态管理
每个节点维护三个关键状态:
- 数据包队列:存储到达的数据包及其到达时间
- 传输队列:当前正在传输的数据包数量
- 连接状态:标识节点是否已建立连接
3. 时延记录机制
- 记录每个数据包的到达时间和完成时间
- 时延 = 完成时间 - 到达时间
- 提供详细的时延分布统计
详细执行流程
初始化阶段
% 节点状态初始化
node_data = cell(Node_num, 1); % 数据包队列(存储到达时间)
transmission_queue = zeros(Node_num, 1); % 传输队列剩余数据包数
node_connected = false(Node_num, 1); % 连接状态标志
主循环(每个时隙)
步骤1:数据包到达
- 每个节点以概率λ接收新数据包
- 记录数据包的到达时隙
- 数据包存储在节点的数据包队列中
步骤2:批次形成
- 检查每个节点的数据包数量
- 如果数据包数量 ≥ M,则有资格形成批次
步骤3:请求发送决策
- 只有满足以下条件的节点才能发送请求:
- 数据包数量 ≥ M(有完整批次)
- 未建立连接(
~node_connected(i)) - 传输队列为空(
transmission_queue(i) == 0)
- 每个合格节点以概率q决定是否发送请求
步骤4:冲突检测
- 如果恰好只有一个节点发送请求,则请求成功
- 成功节点:
- 建立连接(
node_connected = true) - 将M个数据包加入传输队列(
transmission_queue = M) - 记录这M个数据包的到达时间
- 从数据包队列中移除这M个数据包
- 建立连接(
步骤5:传输状态更新
- 对于传输队列不为空的节点:
- 传输一个数据包(传输队列减1)
- 记录该数据包的完成时间(当前时隙)
- 如果传输队列为空,断开连接
时延计算与统计
- 计算每个数据包的时延:
完成时间 - 到达时间 - 统计平均时延、时延范围、标准差、百分位时延等
- 提供详细的调试信息输出
关键设计特点
1. 协议准确性
- 严格遵循CBA协议的核心机制
- 防止正在传输的节点发送新请求
- 正确的批次处理和冲突检测
2. 时延计算精确性
- 精确记录每个数据包的到达和完成时间
- 考虑批次传输的时序特性
- 提供全面的时延分布统计
3. 非饱和条件支持
- 初始状态为空队列
- 动态数据包到达
- 反映真实网络负载情况
4. 调试与验证
- 详细的运行时信息输出
- 传输数据包计数和时延分布
- 便于验证仿真结果的正确性
Main10:
clc;clear;close all;
%% 时延仿真比较:GF vs SAST vs CBA
ACB_bw_simu = [0.0001,0.001:0.001:0.01];
Lambda_total = 1; % 饱和情况
Node_num = 100;
Total_slot = 2e6;
% CBA协议参数
M = 4; % 批次大小
delta = 3; % 信令开销时隙数
% 运行三种协议的时延仿真
delay1_simu = zeros(size(ACB_bw_simu));
delay3_simu = zeros(size(ACB_bw_simu));
delay5_simu = zeros(size(ACB_bw_simu)); % CBA协议
for k = 1:length(ACB_bw_simu)
q = ACB_bw_simu(k);
fprintf('正在进行时延仿真: q=%.4f (%d/%d)\n', q, k, length(ACB_bw_simu));
% GF协议时延仿真
[delay1_simu(k), ~] = GF_delay(q, Lambda_total, Node_num, Total_slot);
% SAST协议时延仿真
[delay3_simu(k), ~] = SAST_delay(q, Lambda_total, Node_num, Total_slot);
% CBA协议时延仿真
[delay5_simu(k), ~] = CBA_delay(q, Lambda_total, Node_num, Total_slot, M, delta);
end
%% 画图 - 时延比较
figure
hold on;
% 颜色配置
figcol = cell(1,3);
figcol{1} = '#336633'; % GF - 绿色
figcol{2} = '#5C0DAC'; % SAST - 紫色
figcol{3} = '#FF8C00'; % CBA - 橙色
% 标记形状配置
figshape = cell(1,3);
figshape{1} = '*';
figshape{2} = 'O';
figshape{3} = 'diamond';
linewidth = 2;
markersize = 80;
% 绘制时延曲线并保存图形对象句柄
h1 = semilogy(ACB_bw_simu, delay1_simu, '-', 'color', figcol{1}, 'LineWidth', linewidth);
h1_scatter = scatter(ACB_bw_simu, delay1_simu, markersize, 'MarkerEdgeColor', figcol{1}, ...
'Marker', figshape{1}, 'LineWidth', linewidth);
h2 = semilogy(ACB_bw_simu, delay3_simu, '--', 'color', figcol{2}, 'LineWidth', linewidth);
h2_scatter = scatter(ACB_bw_simu, delay3_simu, markersize, 'MarkerEdgeColor', figcol{2}, ...
'Marker', figshape{2}, 'LineWidth', linewidth);
h3 = semilogy(ACB_bw_simu, delay5_simu, ':', 'color', figcol{3}, 'LineWidth', linewidth);
h3_scatter = scatter(ACB_bw_simu, delay5_simu, markersize, 'MarkerEdgeColor', figcol{3}, ...
'Marker', figshape{3}, 'LineWidth', linewidth);
hold off;
xlim([0, max(ACB_bw_simu)]);
% 设置中文标签(使用支持中文的字体,关闭latex解释器)
xlabel('传输概率', 'Interpreter', 'none', 'FontName', 'SimHei', 'fontsize', 14);
ylabel('平均时延 (时隙)', 'Interpreter', 'none', 'FontName', 'SimHei', ...
'rotation', 0, 'Horizontalalignment', 'right', 'fontsize', 14);
% 添加中文标题
title('三种协议的时延仿真比较', 'Interpreter', 'none', 'FontName', 'SimHei', 'fontsize', 16);
% 设置图例(只使用线对象,不包括散点对象)
legend([h1, h2, h3], {'GF协议', 'SAST协议', 'CBA协议'}, 'Location', 'best', ...
'Interpreter', 'none', 'FontName', 'SimHei', 'fontsize', 12);
% 设置坐标轴字体(支持中文)
set(gca, 'position', [0.15, 0.15, 0.7, 0.7], 'LineWidth', 0.5, ...
'fontsize', 14, 'FontName', 'SimHei'); % 改为SimHei支持中文
set(gcf, 'unit', 'normalized', 'position', [.2, .2, 0.4, 0.45]);
grid on;
box on;
%% 输出时延分析结果
fprintf('\n=== 时延分析结果 ===\n');
fprintf('协议\t\t平均时延\t最小时延\t最优q值\n');
[~, idx1] = min(delay1_simu);
fprintf('GF\t\t%.2f\t\t%.2f\t\t%.4f\n', mean(delay1_simu), min(delay1_simu), ACB_bw_simu(idx1));
[~, idx3] = min(delay3_simu);
fprintf('SAST\t\t%.2f\t\t%.2f\t\t%.4f\n', mean(delay3_simu), min(delay3_simu), ACB_bw_simu(idx3));
[~, idx5] = min(delay5_simu);
fprintf('CBA\t\t%.2f\t\t%.2f\t\t%.4f\n', mean(delay5_simu), min(delay5_simu), ACB_bw_simu(idx5));
save('delay_comparison.mat');
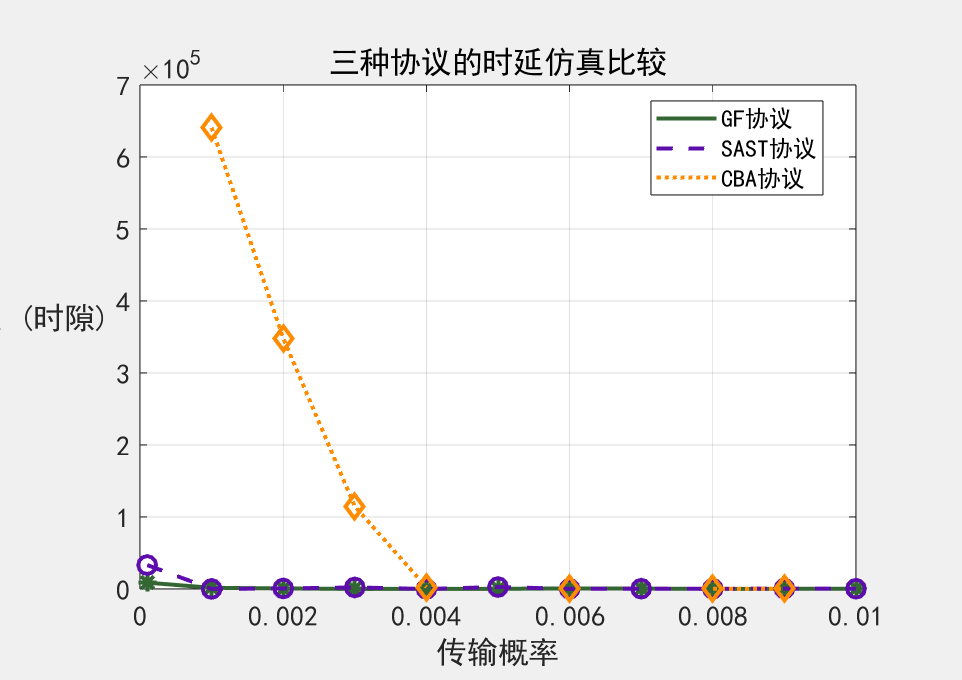
分析:
图中的CBA时延值很大,说明在有限的短时隙里,数据要形成M个才能成功申请传输,其实并不能确保传输完。需要适当调大λ值或q值才能得到很好的仿真效果。
并且,与SAST和slotted Aloha相比,CBA的时延值与二者接近,所以CBA在时延性指标上可以认为效果较好





















 930
930

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








