向量与三角

最新推荐文章于 2020-06-09 20:14:35 发布

原创最新推荐文章于 2020-06-09 20:14:35 发布 · 305 阅读

0 ·

CC 4.0 BY-SA版权

高中数学知识专栏收录该内容

15 篇文章

订阅专栏

[题目]
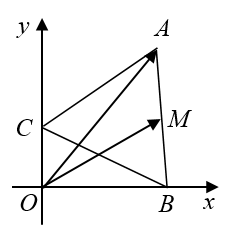
如图，等边 $△ A B C$ 的边长为 $2$ ，顶点 $B, C$ 分别在 $x$ 轴的非负半轴， $y$ 轴的非负半轴上滑动， $M$ 为 $A B$ 中点，则 $OA→⋅OM→\overrightarrow{OA}\cdot\overrightarrow{OM}$ 的最大值为 $()(\qquad)$
$A.7B.52+7C.72D.3+332A.\sqrt{7}\qquad\qquad B.\dfrac{5}{2}+\sqrt{7}\qquad\qquad C. \dfrac{7}{2}\qquad\qquad D. 3+\dfrac{3\sqrt{3}}{2}$

[解析]
如图，设 $∠OBC=θ,θ∈[0,π2]\angle OBC=\theta ,\theta\in[0,\dfrac{\pi}{2}]$ ，则 $OB=2cos⁡θ,OC=2sin⁡θOB=2\cos\theta,OC=2\sin\theta$ .所以 $OA→⋅OM→=(OC→+CA→)⋅(OB→+BM→)=OC→⋅OB→+CA→⋅OB→+OC→⋅BM→+CA→⋅BM→\overrightarrow{OA}\cdot\overrightarrow{OM} =(\overrightarrow{OC}+\overrightarrow{CA})\cdot(\overrightarrow{OB}+\overrightarrow{BM})=\overrightarrow{OC}\cdot\overrightarrow{OB}+\overrightarrow{CA}\cdot\overrightarrow{OB}+\overrightarrow{OC}\cdot\overrightarrow{BM}+\overrightarrow{CA}\cdot\overrightarrow{BM}$ 代入数据得 $OA→⋅OM→=0+2⋅2cos⁡θ⋅cos⁡(π3−θ)+2sin⁡θ⋅1⋅cos⁡(θ−π6)+2⋅1⋅cos⁡π3\overrightarrow{OA}\cdot\overrightarrow{OM}=0+2\cdot2\cos\theta\cdot\cos(\dfrac{\pi}{3}-\theta)+2\sin\theta\cdot1\cdot\cos(\theta-\dfrac{\pi}{6})+2\cdot1\cdot\cos\dfrac{\pi}{3}$ 化简得 $OA→⋅OM→=7sin⁡(2θ+φ)+52\overrightarrow{OA}\cdot\overrightarrow{OM}=\sqrt{7}\sin(2\theta+\varphi)+\dfrac{5}{2}$ 所以 $OA→⋅OM→\overrightarrow{OA}\cdot\overrightarrow{OM}$ 的最大值为 $52+7\dfrac{5}{2}+\sqrt{7}$ .