Leetcode-73. 矩阵置零

给定一个 m x n 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。

示例 1：

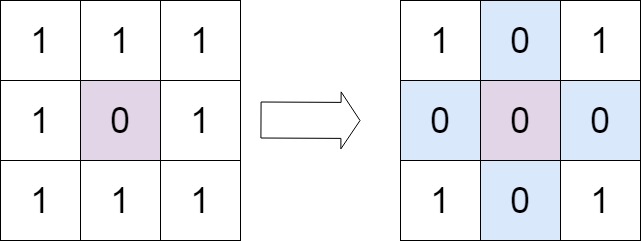
输入：matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出：[[1,0,1],[0,0,0],[1,0,1]]

示例 2：

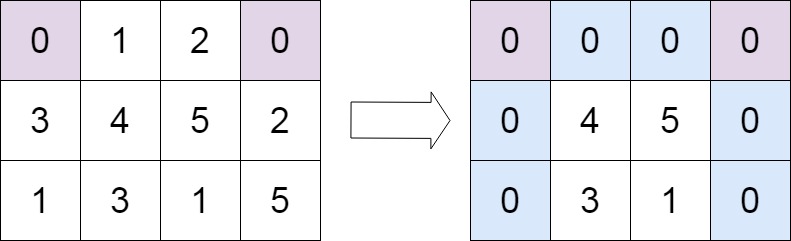
输入：matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出：[[0,0,0,0],[0,4,5,0],[0,3,1,0]]

提示：

• m == matrix.length
• n == matrix[0].length
• 1 <= m, n <= 200
• -231 <= matrix[i][j] <= 231 - 1

方法一：使用一个行数组和一个列数组记录有的行和列，这种方法简单但是没有做到原地使得矩阵置零。

代码：

class Solution {
    public void setZeroes(int[][] matrix) {
        //用set是方便使用其contains方法，不然用list就要遍历一遍
        Set<Integer> r = new HashSet<>();//行
        Set<Integer> l = new HashSet<>();//列
        for(int i = 0;i < matrix.length;i++){
            for(int j = 0;j < matrix[0].length;j++){
                //如果matrix[i][j] == 0，就把其行列加入数组
                if(matrix[i][j] == 0){
                    r.add(i);
                    l.add(j);
                }
            }
        }

        for(int i = 0;i < matrix.length;i++){
            for(int j = 0;j < matrix[0].length;j++){
                //再次遍历，如果其行列在有零的行列，就置为零
                if(r.contains(i) || l.contains(j)){
                    matrix[i][j] = 0;
                }
            }
        }
    }
}

方法二：将第一行列当作方法一的r、lSet集合，所以第一行列是否有零就需要另设置变量记录。还有些小细节看代码。

代码：

class Solution {
    public void setZeroes(int[][] matrix) {
       //记录第一行列是否有零
       boolean ZeroR = false;boolean ZeroL = false;
        //行列数
       int numR = matrix.length;int numL = matrix[0].length;
        //查看第一行是否有零
       for(int i = 0;i < numL;i++){
        if(matrix[0][i]==0){
            ZeroR = true;
            break;
        }
       }
        //查看第一列是否有零
       for(int i = 0;i < numR;i++){
        if(matrix[i][0]==0){
            ZeroL= true;
            break;
        }
       }
       //i=1，j=1，因为第一行列不需要再次遍历
       for(int i = 1;i < numR;i++){
        for(int j = 1;j < numL;j++){
            //如果该数为零，使其行列所在的第一行列记录为0，
            //如果第一行列本来就为0也不影响。
            if(matrix[i][j] == 0){
                matrix[i][0] = 0;
                matrix[0][j] = 0;
            }
        }
       }
       //这里必须先遍历初第一行列的元素
       //原因是如果第一行列有零，就会全部置位0，再遍历处第一行列的元素就会使得整个矩阵为0
       for(int i = 1;i < numR;i++){
        for(int j = 1;j < numL;j++){
            if(matrix[0][j]==0 || matrix[i][0]==0){
                matrix[i][j] = 0;
            }
        }
       }
        //遍历第一行列
       if(ZeroR){
        for(int i = 0;i < numL;i++){
            matrix[0][i] = 0;
        }
       }
       if(ZeroL){
        for(int i = 0;i < numR;i++){
            matrix[i][0] = 0;
        }    
       }
    }
}