对深度学习卷积操作的理解

本文介绍对了对卷积核、滤波器、通道等概念的理解。

二维卷积

二维卷积就是卷积核（指的是一个小的权值矩阵）在二维输入数据上滑动遍历整张图片，对当前输入的部分元素进行矩阵乘法，将一个二维矩阵转换为另一个二维矩阵，然后将结果输出，输出特征实际上是在输入数据相同位置上的加权和。下图是一个标准的卷积：

从上面的描述可知，卷积核的尺寸直接决定了生成新的特征是汇合了多少个输入特征，在上图中，我们输入的特征为5*5， 输出数据为(5-3+1)*(5-3+1)=3*3. 如果我们使用标准的全连接层，就会产生一个25*9=225 个参数的权值矩阵，每个输出都是所有输入数据的加权求和。使用卷积操作我们只用9个参数来实现这个变换，每个输出特性不用查看每个输入特征，而只是查看大致相同位置的输入特征。

常用的卷积技术

1. Padding
   在下面的动画中可以看到卷积核在滑动过程中边缘基本上会被裁剪掉，因为边缘上的像素永远不在卷积核的中心，但是我们通常需要让输出尺寸等于输入尺寸，所以边缘被裁减掉会使输入尺寸丢失。为了解决这个问题，padding使用一些假像素（通常是0）来填充边缘，同事延伸到边缘外的假像素，从而产生与输入相同大小的输出。
   
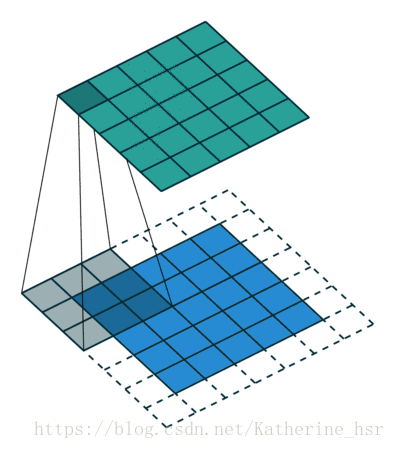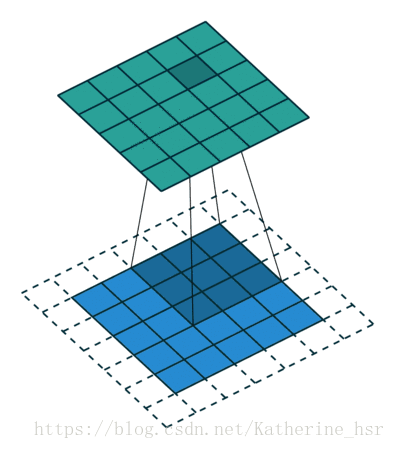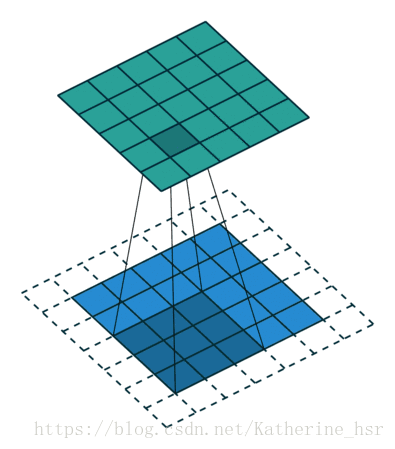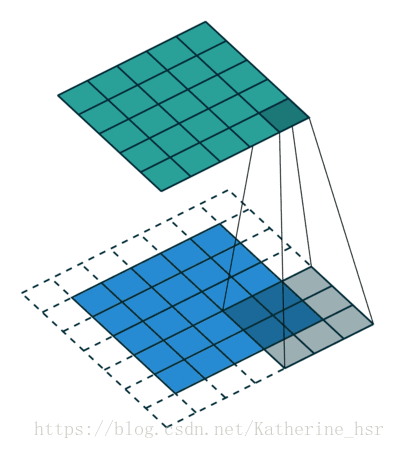
2. Striding
   在运行卷积层时我们通常希望输出尺寸比输入尺寸更低，在增加信道数量的同时将空间尺寸减小。其中一种方法是使用池化层，例如使用2*2的网格的平均值、最大值、最小值将空间维度减小。还有一种方式是striding，基本思想是改变卷积核移动的歩长跳过一些像素。Stride是1表示的是一个标准卷积模式，stride是2表示卷