函数的相关与卷积

原创 蒲山牧: https://www.upsame.com/

信号处理过程中

1. 卷积的定义
   
   卷积满足交换律、分配律、结合律。也具有位移不变性以及缩放性质。

2. 互相关的定义
   

   替换变量后有：
   
   上述两式完全等价。

性质：

• （1）互相关是两个函数间存在相似性的量度。

• （2）由上述（2）式可得：
  

• （3）相关运算和卷积运算的区别：
  对相关来说，f(x)要取复共轭，运算时f(x)不需折叠。

• （4）f(x)和g(x) 做相关 等于 f*(-x) 与 g(x) 做卷积。

• （5）注意互相关不满足交换律。

3. 自相关

   在信号分析当中通常将自相关函数称之为自协方差方程，定义如下：
   
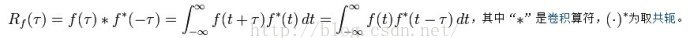
   自相关是互相关的一种特殊情况，就是一个序列和它本身做相关，主要用来衡量一个序列在不同时刻取值的相似程度。

数理统计中

1. 相关：我们通常说的相关系数的学名是—皮尔逊积差系数（Pearson’s product moment coefficient），这种相关系数只对两个变量的线性关系敏感。
   Pearson 相关系数使用两个变量的协方差和标准差来定义：

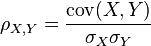
其中，cov 是协方差，sigma 是标准差。因为 cov 可以写作：

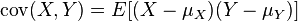
所以 Person 相关系数的定义式可以写作：

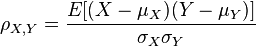
2. 自相关的定义式如下：

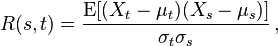
如果随机过程是一个宽平稳过程，那么均值和方差都不是时间的函数，所以，自相关定义式变为：

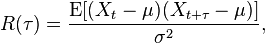
在某些学科中，会去掉归一化因子σ2，使用自协方差来代替自相关。但是归一化因子可以让自相关的取值在 [-1, 1] 之间，不会随着序列的绝对大小而变化。

在信号处理中：
自相关的定义会去掉归一化，即不用减去均值，也不用除以方差。当除以方差时，一般叫做另外一个名字：自相关系数(Autocorrelation coefficient)。

本文由博客 首发于蒲山牧的博客