循环神经网络（RNN）解惑

由来

• 传统的神经网络模型是从输入层到隐含层再到输出层的全连接，且同层的节点之间是无连接，网络的传播也是顺序的

• 但这种普通的网络结构对于许多问题却显得无能为力。例如，在自然语言处理中，如果要预测下一个单词，就需要知道前面的部分单词，因为一个句子中的单词之间是相互联系的，即有语义。这就需要一种新的神经网络，即循环神经网络RNN

• 循环神经网络对于序列化的数据有很强的模型拟合能力。

• 具体的结构为：循环神经网络在隐含层会对之前的信息进行存储记忆，然后输入到当前计算的隐含层单元中，也就是隐含层的内部节点不再是相互独立的，而是互相有消息传递。

• 隐含层的输入不仅可以由两部分组成，输入层的输出和隐含层上一时刻的输出，即隐含层内的节点自连；

• 隐含层的输入还可以由三部分组成，输入层的输出、隐含层上一时刻的输出、上一隐含层的状态，即隐含层内的节点不仅自连还互连。

图解

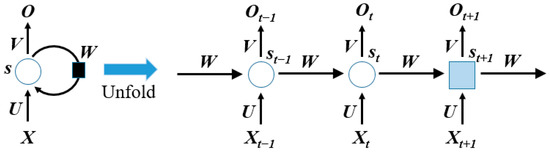
• x：输入序列的单个时间步特征；
• s：隐藏状态（RNN 的 “记忆单元”）；
• o：输出；
• (U、V、W)：权重参数（整个 RNN 共享同一套参数，这是 RNN 的核心特性之一）

以图中 t-1 $\to$ t $\to$ t+1 的链式结构为例

1. 初始状态 (t=0）：设置初始隐藏状态 $s_0$（通常为全 0 向量）；

2. 时间步 t-1：

   • 输入 $x_{t-1}$，结合 $s_0$计算 $s_{t-1}=\tanh (U\cdot x_{t-1}+W\cdot s_0+b_s)$；
   • 计算输出 $o_{t-1}=V\cdot s_{t-1}+b_o$；

3. 时间步 t：

   • 输入 $x_t$，结合 $s_{t-1}$ 计算 $s_t=\tanh (U\cdot x_t+W\cdot s_{t-1}+b_s)$；
   • 计算输出 $o_t=V\cdot s_t+b_o$；

4. 时间步 t+1：

   • 输入 $x_{t+1}$，结合 $s_t$ 计算 $s_{t+1}=\tanh (U\cdot x_{t+1}+W\cdot s_t+b_s)$；
   • 计算输出 $o_{t+1}=V\cdot s_{t+1}+b_o$；

5. 后续时间步：重复上述步骤，直到序列的最后一个时间步 T。

关键特性：参数共享与时序依赖

计算思路体现了 RNN 的两个核心特性：
- 参数共享：所有时间步共用同一套 (U、V、W) 权重，大幅减少了参数数量（对比 “每个时间步单独设计网络” 的方案）；
- 时序依赖：每个时间步的隐藏状态 $s_t$ 包含了 $x_1$ 到 $x_t$ 的所有时序信息，因此 RNN 能捕捉序列中 “当前元素与历史元素的关联”。

相关概念

1. 时间步（Time Step, t）：序列的 “逐个处理单元”

通俗理解

时间步是序列数据的 “最小处理单位”，对应序列中的每个元素。比如：

• 文本序列：“我 / 爱 / 深 / 度 / 学 / 习” → 6 个时间步（每个字为 1 个 t）；
• • 语音序列：1 秒语音 → 按 10ms 分割为 100 个时间步（每个片段为 1 个 t）；
• • 时间序列：10 天的气温 → 10 个时间步（每天为 1 个 t）。

技术定义

设输入序列为 $X=[x_1,x_2,...,x_T]$，其中：

• T 是序列总长度（总时间步）；
• $x_t$ 是第 t 个时间步的输入（维度：[batch_size, input_dim]，batch_size 为批量大小，input_dim 为输入特征数）。

2. 隐藏状态（Hidden State, $h_t$）：RNN 的 “记忆单元”

通俗理解

隐藏状态是 RNN 的 “核心记忆”，存储了从第 1 个时间步到第 t 个时间步的所有关键信息。它就像你的 “大脑工作内存”：

• 阅读时，$h_t$ 是你读到第 t 句话时的 “剧情记忆”；
• 处理语音时，$h_t$ 是你听到第 t 个片段时的 “语音特征记忆”；
• 关键特性：每个时间步的 $h_t$ 都依赖于上一个时间步的 $h_{t-1}$（记忆传承）。

技术定义

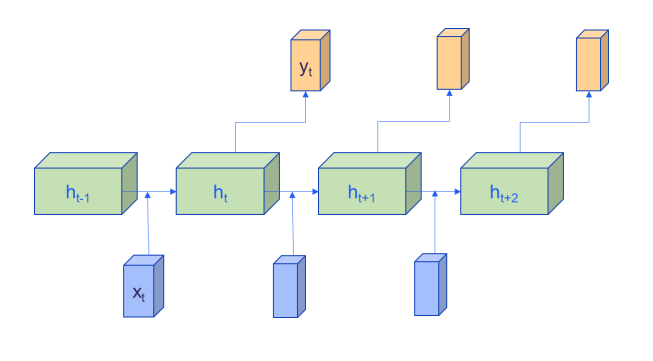
RNN 的隐藏状态更新公式（Elman RNN，最基础的 RNN）：

$h_t=\tanh (W_{xh}{x}_t+W_{hh}{h}_{t-1}+b_h)$

各参数含义：

• $h_t$ ：第 t 个时间步的隐藏状态（维度：[batch_size, hidden_dim]，hidden_dim 为隐藏层维度，可自定义）；
• $h_0$ ：初始隐藏状态（t=0 时，默认全 0 或随机初始化）；
• $W_{xh}$：输入到隐藏层的权重（维度：[input_dim, hidden_dim]）；
• $W_{hh}$：隐藏层到自身的权重（维度：[hidden_dim, hidden_dim]）→ 核心！实现 “记忆传承”；
• $b_h$：隐藏层偏置（维度：[hidden_dim]）；
• $tanh$：激活函数（将输出压缩到 [-1,1]，避免梯度爆炸）。

3. 时序依赖（Temporal Dependency）：RNN 的 “核心目标”

通俗理解

时序依赖是序列数据中 “当前元素与过去元素的关联”。比如：

• 文本：“他昨天去了北京，___今天在故宫玩” → 空格处的词依赖 “北京”“昨天”（时序依赖）；
• 语音：识别 “我爱深度学习” 时，“学” 的发音依赖前面 “深” 的发音（连读现象）；
  时间序列：预测明天的气温，依赖过去 7 天的气温趋势（时序依赖）。

技术定义

时序依赖通过隐藏状态的 “迭代更新” 实现：

• 第 t 个时间步的 $h_t$ 依赖 $h_{t-1}$，而 $h_{t-1}$ 依赖 $h_{t-2}$，最终追溯到 $h_0$ 和 $x_1$；
• 因此，$h_t$ 间接包含了 $x_1$ 到 $x_t$ 的所有时序信息，RNN 通过学习 $W_{xh}$ 和 $W_{hh}$ 的权重，自动捕捉序列中的 “长短期依赖”（理想情况下）。