LayerNorm 的计算逻辑

要理解 LayerNorm，核心是抓住它和 BatchNorm 的核心差异：LayerNorm 是 “按样本、跨通道” 计算统计量（而 BatchNorm 是 “按通道、跨样本”）

可视化计算

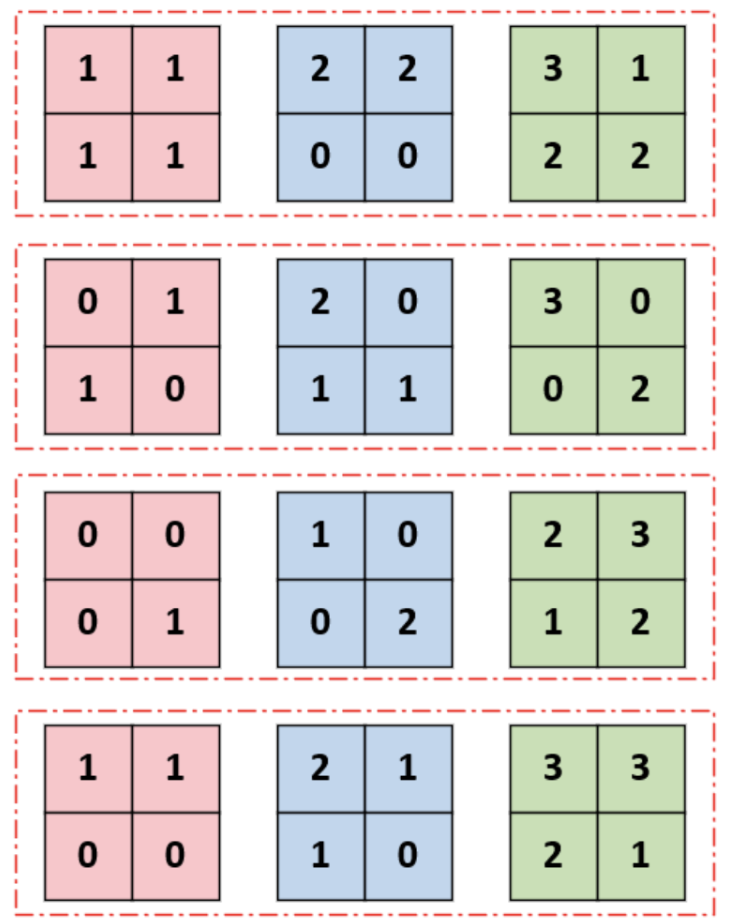
还是以这个图为例（[Batch=3, Channel=4, H=2, W=2]），该图有3个样本(“样本” 是 “1 列的 4 个小矩阵”)，每个样本内部有 4 个独立的 “信息通道”，每个通道对应一个 2×2 的特征图（比如通道 1 可能是 “边缘特征”，通道 2 可能是 “纹理特征”）

LayerNorm 的计算逻辑是：对每个样本（1 列的 4 个通道），合并所有通道的元素值算均值 / 方差，再归一化该样本的所有元素。

步骤 1：选 1 个样本（比如第 1 列的样本 1：4 个通道的 2×2 矩阵）

样本 1 的 4 个通道数据：

• 通道 1：[[1,1],[1,1]] → 元素：1,1,1,1
• 通道 2：[[0,1],[1,0]] → 元素：0,1,1,0
• 通道 3：[[0,0],[0,1]] → 元素：0,0,0,1
• 通道 4：[[1,1],[0,0]] → 元素：1,1,0,0

步骤 2：合并该样本的所有通道元素（共 4 通道 ×2×2=16 个值）

收集样本 1 的所有元素：
[1,1,1,1, 0,1,1,0, 0,0,0,1, 1,1,0,0]

步骤 3：计算该样本的均值和标准差

• 均值 μ = (1+1+1+1+0+1+1+0+0+0+0+1+1+1+0+0) / 16 = 8 / 16 = 0.5
• 方差 σ² = [(1-0.5)²×4 + (0-0.5)²×4 + (1-0.5)²×4 + (0-0.5)²×4] / 16 ≈ 0.25
• 标准差 σ = √0.25 = 0.5

步骤 4：对该样本的所有元素逐个归一化

用公式 (元素值 - μ) / (σ + ε) 替换样本 1 的所有元素：
1 → (1-0.5)/0.5 = 1
0 → (0-0.5)/0.5 = -1

归一化后的样本 1：

• 通道 1：[[1,1],[1,1]]
• 通道 2：[[-1,1],[1,-1]]
• 通道 3：[[-1,-1],[-1,1]]
• 通道 4：[[1,1],[-1,-1]]

LayerNorm 的核心特点

• 按样本独立计算：每个样本（第 1/2/3 列）都有自己的均值 / 方差，互不干扰；
• 跨通道统计：每个样本的所有通道（4 行）数据合并计算，不区分通道类型；
• 不依赖 Batch：哪怕 Batch=1（只有 1 个样本），LayerNorm 也能正常计算（而 BatchNorm 会失效）；
• 适用于变长数据：比如文本序列（每个样本长度不同），LayerNorm 可以对每个样本单独归一化（而 BatchNorm 需要固定 Batch 内的样本长度）。

LayerNorm 是 “给单个样本做‘全身检查’：把这个样本的所有特征（所有通道）的数据合并，算整体的均值 / 方差，再把每个特征值都调整到标准分布”—— 它不关心有多少个样本（Batch），只关心 “当前这一个样本的所有特征是否分布稳定”。

混淆点

为什么 BatchNorm 不按列算？

• BatchNorm 和 LayerNorm 适用场景差异的核心——不是 “不能按列（样本）算”，而是 “按列算是否符合任务的特征逻辑”
• 按列（样本）算” 是 LayerNorm 的逻辑，但它适用于 “通道是连续特征” 的场景

举个栗子

• “通道 1 是边缘、通道 2 是纹理，混在一起破坏独立性”，是图像 / CNN 任务的特征逻辑（每个通道是独立的 “局部特征”），所以 BatchNorm “按通道算” 更合理；
• 但在文本 / Transformer 任务中，通道（比如词向量的维度）是 “同一个词的不同语义特征”（不是独立的，而是互补的），此时 “按样本跨通道算” 反而更合理。

总结

• 因为 BatchNorm 是为图像 / CNN 任务设计的，而这类任务的通道是 “独立的局部特征”—— 按列算会破坏不同通道的语义独立性，所以 BatchNorm 选择 “按通道（行）算”；
• 但 LayerNorm 是为文本 / 序列任务设计的，这类任务的通道是 “同一对象的语义维度”—— 按列算不仅不会破坏特征，反而能稳定同一对象的语义分布，所以 LayerNorm 选择 “按样本（列）算”