HMM-ANN hybird models（隐马尔可夫和神经网络的混合模型）推导

将神经网络（ANN）集成到隐马尔可夫模型（HMM）框架中的语音识别（STT）模型，核心是用神经网络替代 HMM 传统的 “发射概率模型”（Emission Model），以提升建模能力。

相关概念

• 隐藏状态：语音的基本单元（比如音素、音节）；
• 可观测数据：语音的声学特征（比如 MFCC 特征，是从语音信号中提取的数值向量）；
• 发射概率模型：给定 “音素 A” 这个隐藏状态时，观测到 “某组 MFCC 特征” 的概率（即 P (声学特征 | 音素 A)）。

为什么要做 HMM-ANN 混合？

传统 HMM-GMM 模型的缺陷：

• 用高斯混合模型（GMM） 做 “发射概率模型”（即：给定 HMM 的隐藏状态，观测到声学特征的概率）；
• GMM 是 “浅层模型”，难以捕捉声学特征的复杂非线性模式（比如语音的时变、上下文依赖）。

因此，用神经网络（ANN，包括 MLP、LSTM 等） 替代 GMM 作为发射模型，利用神经网络的非线性拟合能力，提升 HMM 对声学特征的建模精度。

混合模型的结构与优势

结构：

• HMM 负责 “时序建模”（处理语音的序列依赖），神经网络负责 “发射概率建模”（处理声学特征的复杂模式），两者分工明确；

优势：

• 保留 HMM 的时序建模能力（适合语音这种序列数据）；
• 用神经网络替代 GMM，提升对声学特征的拟合精度（能捕捉非线性、上下文关联的特征）；
• 支持多种神经网络架构：从简单的 MLP 到复杂的 LSTM（处理语音的长时依赖）。

HMM-ANN 混合模型是 “HMM 管时序，神经网络管声学特征” 的语音识别模型：先借 HMM-GMM 得到 “声学特征 - 隐藏状态” 的对齐标签，再用神经网络学习这个对齐关系，最终用神经网络替代 GMM 作为 HMM 的发射概率模块，兼顾了 HMM 的时序建模和神经网络的特征拟合能力。

HMM-ANN 混合模型的架构图（出自 Kipyatkova 和 Karpov 2016 年的研究）

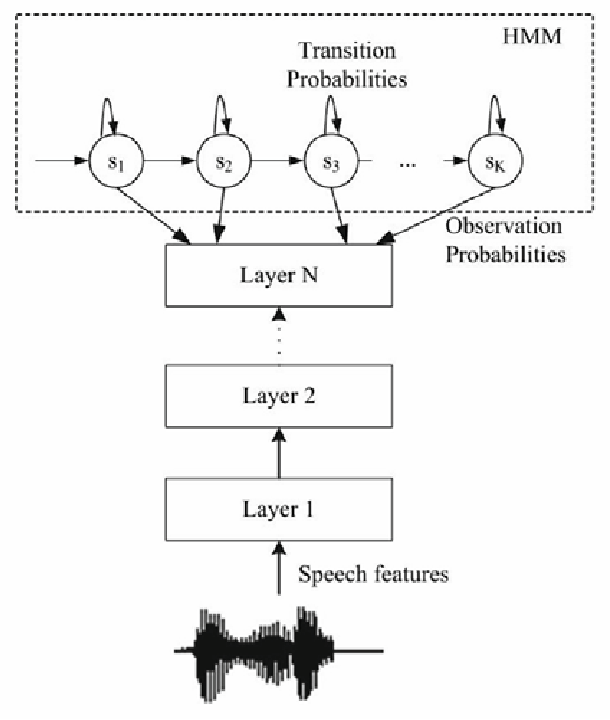
输入层：

• 输入为 “Speech features”（语音特征，如 MFCC），是从原始语音信号中提取的数值特征。

神经网络（ANN）部分：

• 包含多层（Layer 1 到 Layer N），通常是 MLP、LSTM 等结构；
• 功能是将语音特征映射为 “观测概率”（Observation Probabilities），即给定语音特征时，对应 HMM 隐藏状态的概率（替代传统 HMM 的 GMM 发射概率模型）。

HMM 部分：

• 由多个 “隐藏状态”（S₁到 Sₖ）组成，代表语音的基本单元（如音素）；
• 包含 “转移概率”（Transition Probabilities），描述隐藏状态之间的时序转移规则；
• 接收神经网络输出的观测概率，通过 HMM 的时序建模能力，最终得到最优的隐藏状态序列（对应识别出的语音内容）。

该架构的本质是 “ANN 负责声学特征建模，HMM 负责时序建模”：

• 利用神经网络的非线性拟合能力，更精准地计算 “语音特征→隐藏状态” 的观测概率；
• 利用 HMM 的时序特性，处理语音的序列依赖关系，实现从 “特征序列” 到 “语音单元序列” 的转换

举个例子

以识别文本“机器学习是人工智能的核心技术”为例，拆解 HMM-ANN 的工作流程

假设 HMM 的隐藏状态 k 对应汉语普通话的 41 个音素，因此神经网络 Layer N 的输出维度为 41（“41” 是语音识别系统中 “人为定义的音素集合大小”，是工程实践中的经验选择）

步骤 1：语音输入与特征提取

• 输入：朗读 “机器学习是人工智能的核心技术” 的语音信号（图中底部声波）；
• 处理：将语音切分为10ms / 帧的短时片段，每帧提取 MFCC 声学特征（共得到约 200 帧特征，对应整个句子的时长）。

步骤 2：神经网络输出观测概率（Layer N 的 41 维输出）

神经网络（Layer 1~N）对每帧特征做处理，输出41 维的观测概率向量（对应 41 个音素的匹配度）：

• 第 1 帧特征 → 输出向量：[0.01（音素 “j”）, 0.92（音素 “ī”）, 0.03（音素 “q”）, ..., 0.00（其他音素）] → 代表这一帧最可能对应音素 “ī”；
• 第 5 帧特征 → 输出向量：[0.88（音素 “x”）, 0.02（音素 “j”）, ..., 0.00] → 代表这一帧最可能对应音素 “x”；
• （所有 200 帧特征都会生成对应的 41 维概率向量，即图中的 “Observation Probabilities”）。

步骤 3：HMM 的时序建模（k=41 的隐藏状态序列）

HMM 包含41 个隐藏状态（对应 41 个音素），以及音素间的转移概率（比如 “j”→“ī” 的转移概率 0.95，“x”→“ué” 的转移概率 0.88）：

1. 接收每帧的 41 维观测概率；
2. 同时考虑 “观测概率” 和 “转移概率”，对 200 帧特征做时序匹配：
   • 比如第 1-3 帧的观测概率匹配 “j→ī→q”（对应 “机” 的音素）；
   • 第 4-6 帧的观测概率匹配 “x→ué→x”（对应 “学” 的音素）；
     （依次匹配出 “机 - 器 - 学 - 习 - 是 - 人 - 工 - 智 - 能 - 的 - 核 - 心 - 技 - 术” 对应的所有音素序列）；
3. 选择总概率最高的音素序列（即最符合声学特征 + 音素衔接规则的组合）。

步骤 4：输出最终文本

HMM 输出的 41 维隐藏状态序列（音素序列），被映射为汉字序列，最终得到识别结果：“机器学习是人工智能的核心技术”。

HMM的核心作用

HMM 不是对单帧独立判断，而是对 “所有帧的概率序列” 做 “全局最优的时序整合”—— 它的核心作用是 “合并连续的相同音素片段、剔除噪声帧、衔接不同音素”，最终输出无重复、连贯的音素序列。

一、先明确核心前提：HMM 的 “状态”=“音素”，“转移”=“音素切换”

• HMM 的 41 个隐藏状态（S₁~S₄₁）= 41 个音素（比如 S₁=j，S₂=q，S₁₀=x）；
• HMM 的 “状态转移” = 音素之间的切换（比如 S₁→S₁：保持当前音素 j；S₁→S₂：从 j 切换到 q；S₁→S₁₀：从 j 切换到 x）；
• 转移概率规则：
  1. 自转移概率极高（比如 S₁→S₁的概率 = 0.9）：代表 “一个音素会连续占用多帧”（符合发音逻辑：发 “j” 时，连续 5 帧都是 j 的发音）；
  2. 跨状态转移概率较低（比如 S₁→S₂的概率 = 0.05）：代表 “音素切换不频繁”（发音不会每秒切换几十次）；
  3. 无效转移概率为 0（比如 S₁→S₄₁的概率 = 0）：代表 “无意义的音素切换不会发生”（比如 j 不会直接跳到 er）。

二、用 “第 1~5 帧都是 j” 的例子，看 HMM 的组合筛选过程

假设第 1 ~ 5 帧的 41 维向量中，“j（S₁）” 的概率都是最高（0.8~0.9），其他音素概率接近 0。HMM 用 Viterbi 算法做 “全局路径选择”，步骤如下：

步骤 1：初始化（第 1 帧）

计算 “第 1 帧属于每个音素” 的初始概率：

• 属于 S₁（j）的概率 = 初始概率（假设 0.1） × 观测概率（0.9）= 0.09；
• 属于 S₂（q）的概率 = 初始概率（0.1） × 观测概率（0.01）= 0.001；
• 其他音素的概率 ≈ 0；

最优路径（第 1 帧）：选择概率最高的 S₁（j）。

步骤 2：递推（第 2 帧）

对每个音素，计算 “从第 1 帧的最优路径转移到当前音素” 的总概率：

• 情况 1：第 2 帧仍选 S₁（j）→ 总概率 = 第 1 帧 S₁的概率（0.09） × 自转移概率（0.9） × 第 2 帧 S₁的观测概率（0.85）≈ 0.09×0.9×0.85≈0.06885；
• 情况 2：第 2 帧切换到 S₂（q）→ 总概率 = 第 1 帧 S₁的概率（0.09） × 转移概率（0.05） × 第 2 帧 S₂的观测概率（0.01）≈ 0.09×0.05×0.01≈0.000045；

最优路径（第 2 帧）：选择情况 1（继续留在 S₁），总概率 0.06885（远高于切换到其他音素）。

步骤 3：递推（第 3~5 帧）

每帧都重复步骤 2 的逻辑：

• 第 3 帧：留在 S₁的总概率 = 第 2 帧 S₁的概率（0.06885）×0.9×0.88≈0.054；切换到其他音素的概率≈0；
• 第 4 帧：留在 S₁的总概率≈0.054×0.9×0.82≈0.040；
• 第 5 帧：留在 S₁的总概率≈0.040×0.9×0.86≈0.031；

最优路径（第 3~5 帧）：始终选择 “留在 S₁（j）”，因为切换到其他音素的概率太低。

步骤 4：终止（第 5 帧结束）

• 第 1~5 帧的最优路径是：S₁→S₁→S₁→S₁→S₁（连续 5 帧都是 j）；
• HMM 对路径做 “去重合并”：连续的相同状态（S₁）只保留 1 个，即 “第 1~5 帧合并为 1 个音素 j”。

三、为什么不会重复？—— HMM 的 “路径合并” 逻辑

HMM 的输出不是 “每帧的音素判断结果”，而是 “最优路径对应的状态序列”，再通过 “合并连续相同状态” 得到最终音素序列：

• 比如第 1~5 帧的路径是 S₁→S₁→S₁→S₁→S₁ → 合并为 “j”（1 个音素）；
• 第 6~9 帧的路径是 S₁₀→S₁₀→S₁₀→S₁₀（x 的状态） → 合并为 “x”（1 个音素）；

最终 200 帧的路径 → 合并为 30 个左右的音素（无重复、连贯）。

四、再举一个 “含噪声帧” 的例子，看 HMM 的筛选能力

假设第 3 帧是噪声帧：41 维向量中 “q（S₂）” 的概率最高（0.6），j 的概率降到 0.3。HMM 的处理逻辑：

第 3 帧递推时：

• 留在 S₁（j）的总概率 = 第 2 帧 S₁的概率（0.06885）×0.9×0.3≈0.0186；
• 切换到 S₂（q）的总概率 = 第 2 帧 S₁的概率（0.06885）×0.05×0.6≈0.00207；

最优路径仍选择 “留在 S₁（j）”（0.0186 > 0.00207）；

最终第 1~5 帧仍合并为 “j”，噪声帧被 HMM “忽略”（因为切换音素的总概率更低）。

HMM 就像一个 “严格的编辑”，拿到 200 帧的 “音素候选稿” 后，会：

• 把连续重复的 “j” 删掉多余的，只留 1 个；
• 把无关的噪声 “q” 删掉；
• 把音素按合理顺序排列（j→ī→q→ì）；

最终输出一篇 “通顺的音素短文”。

HMM-ANN 混合模型中概率转换推导

核心是解决 “神经网络输出与 HMM 解码需求不匹配” 的问题，以下是结构化解读：

1. 核心矛盾：神经网络输出与 HMM 需求的差异

• 神经网络（分类器）的输出：P(hidden|acoustic)

  • P(hidden|acoustic)：给定声学特征（acoustic），这个特征对应某个隐藏状态（hidden）的概率，即听到某个声音特征，它是某个音素的概率
  • hidden：HMM 的隐藏状态 = 语音的音素（比如 j、q，对应前文的 41 个音素）；
  • acoustic：声学特征 = 从语音中提取的 MFCC（比如前文 “机” 的第 3 帧 MFCC）；
  • P(hidden|acoustic) 是 神经网络（ANN）的输出结果，具体过程：
    • 神经网络的输入：第 3 帧 MFCC（一串数值）；
    • 神经网络的输出：41 个概率值（对应 41 个音素）；
    • 每个输出值就是 P(对应音素|当前MFCC)—— 比如输出层第 1 个神经元对应音素 j，输出 0.9，就是 P(j|A)=0.9。

• HMM 解码（如 Viterbi 算法）需要的输入：P(acoustic|hidden)（发射概率，给定隐藏状态时，对应声学特征的概率）。

  • P(acoustic|hidden) 是 “给定某个隐藏状态（hidden），这个状态生成某个声学特征（acoustic）的概率”，即**“发某个音素时，能产生某个声音特征的概率”**。
  • 核心区别于 P(hidden|acoustic)：
    → P(hidden|acoustic)：先听声音特征 → 猜是哪个音素（“听声辨音”、神经网络输出）；
    → P(acoustic|hidden)：先定音素 → 猜会发出什么声音特征（“发音生声”、HMM 需要的发射概率）。

2. 概率转换的推导（贝叶斯公式）

通过贝叶斯定理将两者关联：

$P(\text{acoustic}|\text{hidden})=\frac{P(\text{hidden}|\text{acoustic})\cdot P(\text{acoustic})}{P(\text{hidden})}$
​

其中：

• P(acoustic)：声学特征本身的概率（对固定输入的声学特征，该值是常数）；
• P(hidden)：隐藏状态的先验概率（可通过训练数据中隐藏状态的出现频率估计）。

3. 简化：解码时只需计算 “缩放后的概率”

由于解码过程中声学特征是固定的（P(acoustic)为常数），因此：

$\frac{P(\text{hidden}|\text{acoustic})}{P(\text{hidden})}\propto P(\text{acoustic}|\text{hidden})$

• 含义：无需计算完整的P(acoustic∣hidden)，只需计算P(hidden|acoustic)/P(hidden)的比值，即可等价替代发射概率用于 HMM 解码。

用前文识别‘机’（音素序列j→ī）的例子

1. 已知条件（前文对应数据）

• 声学特征（acoustic）：“机” 的第 1~5 帧 MFCC（固定输入，P(acoustic)为常数）；
• 隐藏状态（hidden）：音素j（HMM 的状态 S₁）；
• 神经网络输出：P(j|acoustic)=0.9（第 3 帧 MFCC 对应音素j的概率）；
• 隐藏状态先验概率：P(j)通过训练数据估计为 0.05（音素j在训练集中的出现频率）。

即

• P(j|A) = 0.9 → 听特征 A，是音素 j 的概率 90%（神经网络输出）；
• P(j) = 0.05 → 音素 j 在训练集中的出现频率（先验概率）；
• P(A) → 特征 A 本身的概率（固定常数，无需具体值）。

2. 概率转换计算

计算 P(A|j)（音素 j 生成特征 A 的概率）：

根据贝叶斯公式：

$P(\text{acoustic}|j)=\frac{P(j|\text{acoustic})\cdot P(\text{acoustic})}{P(j)}$
​
代入数据：

$P(\text{A}|j)=P(\text{acoustic}|j)=\frac{0.9\cdot P(\text{acoustic})}{0.05}=18\cdot P(\text{acoustic})=18\cdot P(A)$
​→ “当发 j 这个音素时，产生第 3 帧 MFCC（A）的概率，是 P(A) 的 18 倍”。

再计算 P(A|q)（音素 q 生成特征 A 的概率）：

已知：

• P(q|A) = 0.01 → 听特征 A，是音素 q 的概率 1%；
• P(q) = 0.02 → 音素 q 的先验概率。

代入公式：

$P(A|q)=\frac{0.01\times P(A)}{0.02}=0.5\times P(A)$
→ “当发 q 这个音素时，产生特征 A 的概率，是 P(A) 的 0.5 倍”。

3. 解码时的简化处理

由于P(acoustic)是固定常数（当前输入的声学特征概率不变），因此：

​$\frac{P(j|\text{acoustic})}{P(j)}=\frac{0.9}{0.05}=18$

这个比值（18）与P(acoustic|j)成正比（仅差常数P(acoustic)），因此在 HMM 的 Viterbi 解码中，直接用 18 替代P(acoustic|j)参与计算即可。

4. 对应到 HMM 解码的实际作用

HMM 的本质是 “模拟发音过程”：先有音素序列（j→ī→q→ì），每个音素 “发射” 出对应的 MFCC 特征，最终形成连续的语音。

P(acoustic|hidden) 就是这个 “发射” 过程的概率规则 —— 它告诉 HMM：

• 发 j 时，很大概率会产生特征 A（18×P(A)）；
• 发 q 时，产生特征 A 的概率很小（0.5×P (A)）。

因此，当 HMM 看到特征 A 时，会根据这个概率判断：“这个特征更可能是 j 发射的，而不是 q”—— 这就是 HMM 合并第 1~5 帧为音素 j 的核心依据。

HMM 解码时会选择比值更高的音素（18 > 0.5），因此判断当前声学特征对应的隐藏状态是j—— 这与前文 HMM 合并第 1~5 帧为音素j的逻辑完全一致。