BatchNorm 的计算逻辑-优快云博客

0、准备工作

均值和标准差的计算公式如下（代码中均值用mean表示，标准差用std表示）:
均值： $μ=1nΣi=1nxi\ \mu = \frac{1}{n} \Sigma_{i=1}^{n} x_i$

标准差： $σ=1nΣi=1n(xi−μ)2\ \sigma = \sqrt{ \frac{1}{n} \Sigma_{i=1}^{n} (x_i - \mu)^2 }$

1、BatchNorm 计算过程

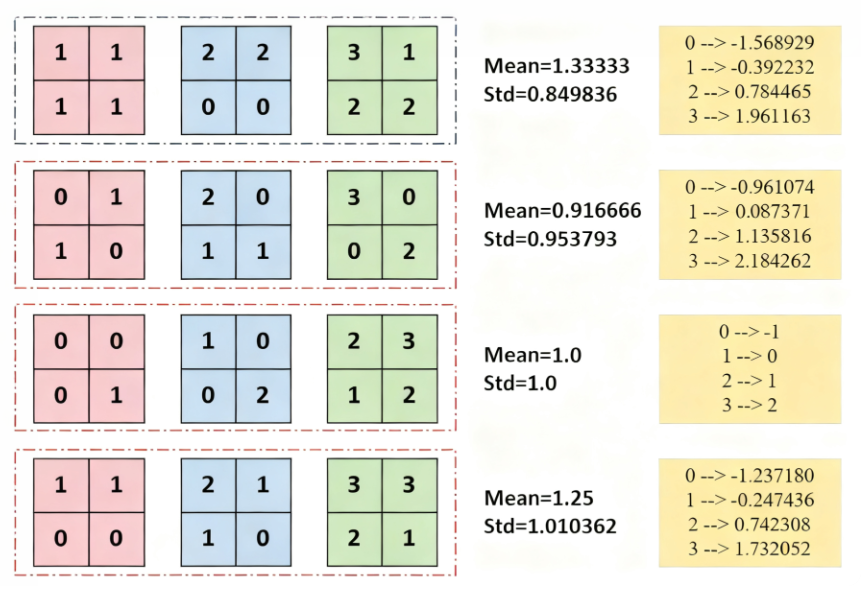
上图有3个样本(“样本” 是 “1 列的 4 个小矩阵”)，每个样本内部有 4 个独立的 “信息通道”，每个通道对应一个 2×2 的特征图（比如通道 1 可能是 “边缘特征”，通道 2 可能是 “纹理特征”）

图中输入的维度是：[Batch=3, Channel=4, Height=2, Width=2]，

Batch=3：3 个样本打包成 1 个批次
Channel=4：共 4 行（每行对应 1 个通道）
Height=2, Width=2：每个 “子特征图” 是 2×2 的矩阵

以 “第 1 个通道” （第 1 行）为例

步骤 1：收集 “该通道 + 整个批次” 的所有特征值

Batch=3，每个样本是 2×2 矩阵，共3×2×2=12个值：

第 1 个样本（粉色）：[1, 1, 1, 1]（对应 “边缘特征强”）；
第 2 个样本（蓝色）：[2, 2, 0, 0]（对应 “边缘特征有强有弱”）；
第 3 个样本（绿色）：[3, 1, 2, 2]（对应 “边缘特征中等”）；
合并所有值：[1,1,1,1, 2,2,0,0, 3,1,2,2]。Std）：

步骤 2：计算该通道的 “均值（Mean）” 和 “标准差（Std）”

这一步是 BatchNorm 的 “统计阶段”，目的是得到该通道特征的整体分布：

均值：所有值的平均 → (1+1+1+1+2+2+0+0+3+1+2+2) / 12 = 16 / 12 ≈ 1.33333（对应图中第一行的Mean=1.33333）；
方差：先算每个值与均值的差的平方和，再除以 12：
( (1-1.333)²×4 + (2-1.333)²×2 + (0-1.333)²×2 + (3-1.333)² + (1-1.333)² + (2-1.333)²×2 ) / 12 ≈ 0.7222；
标准差：√0.7222 ≈ 0.849836（对应图中第一行的Std=0.849836）

步骤 3：对该通道的每个值做 “归一化”

用公式 (原始值 - 均值) ÷ (标准差 + ε)（ε 是极小值，避免除零），把所有值缩放到 “均值 0、方差 1” 的分布：

原始值0：(0 - 1.33333) ÷ 0.849836 ≈ -1.568929（对应图右侧的0 --> -1.568929）；
原始值1：(1 - 1.33333) ÷ 0.849836 ≈ -0.392232（对应1 --> -0.392232）；
原始值2：(2 - 1.33333) ÷ 0.849836 ≈ 0.784465（对应2 --> 0.784465）；
原始值3：(3 - 1.33333) ÷ 0.849836 ≈ 1.961163（对应3 --> 1.961163）。

0、1、2、3 就是左侧特征图里的 “原始数字”，是归一化前的输入数据
BatchNorm 的目标是让同一通道的所有元素分布稳定在均值 0、方差 1—— 每个元素代表 “某个样本的某个位置的特征强度”，只有逐个替换，才能保证每个位置的特征都被归一化到标准分布，避免因批量处理导致的分布偏差。

其他通道的计算逻辑`完全相同`

以第 2 个通道（第 2 行，比如 “纹理特征”）为例：

收集该通道的 12 个值，计算得到Mean=0.916666、Std=0.953793；
对每个值用 (x - 0.916666) ÷ 0.953793 归一化，得到右侧的结果（比如0 --> -0.961074）

第 3 行的特殊情况（Mean=1.0，Std=1.0）

第 3 行的统计结果刚好是Mean=1.0、Std=1.0，所以归一化公式简化为 x - 1.0：

原始值0 → 0-1=-1；
原始值1 → 1-1=0；
原始值2 → 2-1=1；
原始值3 → 3-1=2；
这是巧合，实际场景中很少出现，但能更直观看到归一化的效果

BatchNorm 的核心逻辑「按通道分组，跨样本统计」

行 = 通道（第 1 行 = 通道 1，第 2 行 = 通道 2，共 4 个通道）；
列 = 样本（第 1 列 = 样本 1，第 2 列 = 样本 2，共 3 个样本）；
每个小矩阵 = 1 个样本的 1 个通道的特征图。

BatchNorm 的计算是按通道分组的：对每个通道，收集 “该批次内所有样本在这个通道的特征值”，计算均值 / 方差，再对这些值做归一化。

BatchNorm 的计算目标是：让 “同一类特征（同一通道）” 在 “所有样本（整个批次）” 上的分布稳定—— 所以必须 “按行（通道）收集所有样本的数据，计算统计量”。

BatchNorm 的 “Batch” 体现在 “跨样本统计”（用 Batch 里的 3 个样本的数据），“Norm” 体现在 “按通道归一化”（每行单独算均值方差）—— 按行算，是为了保证同一类特征的统计一致性；跨样本算，是为了保证统计量的稳定性。

3、常见混淆点

为什么不按列（样本）算？

如果按列（样本）算，比如第 1 列（样本 1）：

收集 “样本 1 的通道 1、通道 2、通道 3、通道 4” 的 16 个值（4 个通道 ×2×2），算均值方差；
归一化后，样本 1 的所有通道特征会被混在一起统计 —— 但通道 1 是 “边缘特征”，通道 2 是 “纹理特征”，两者含义完全不同，混在一起统计会破坏特征的独立性，模型根本学不到有用的规律。

而按行（通道）算的核心意义：同一通道是同一类特征，跨样本统计能反映这类特征的整体分布；不同通道是不同类特征，必须分开统计。

用「处理流程动画」理解 Batch=3 的计算

假设 GPU 处理你的图时，步骤是这样的（可视化）：

加载批次数据：同时把「样本 1（粉色列 4 个矩阵）、样本 2（蓝色列 4 个矩阵）、样本 3（绿色列 4 个矩阵）」加载到内存；
并行计算每个样本的所有通道：
- 对样本 1：计算通道 1、通道 2、通道 3、通道 4 的特征值；
- 对样本 2：同时计算它的 4 个通道；
- 对样本 3：同时计算它的 4 个通道；
BatchNorm 统计：
- 对通道 1：收集 “样本 1 通道 1 + 样本 2 通道 1 + 样本 3 通道 1” 的 12 个值，算均值 / 方差；
- 对通道 2：收集 3 个样本的通道 2 数据，算均值 / 方差；
  （4 个通道依次统计）；
输出结果：同时输出 3 个样本归一化后的 4 个通道特征图。