Probabilistic Graphical Model (PGM) 概率图模型框架详解

往期文章链接目录

Probabilistic Graphical Model (PGM)

Definition: A probabilistic graphical model is a probabilistic model for which a graph expresses the conditional dependence structure between random variables.

In general, PGM obeys following rules:
$$\begin{array}{rl}& \text{Sum Rule : }p\left(x_1\right)=\int p\left(x_1,x_2\right)d{x}_2\\ & \text{Product Rule : }p\left(x_1,x_2\right)=p\left(x_1|x_2\right)p\left(x_2\right)\\ & \text{Chain Rule: }p\left(x_1,x_2,\cdots ,x_p\right)=\prod _{i=1}^{p}p\left(x_i|x_{i+1,x_{i+2}}\dots x_p\right)\\ & \text{Bayesian Rule: }p\left(x_1|x_2\right)=\frac{p\left(x_2|x_1\right)p\left(x_1\right)}{p\left(x_2\right)}\end{array}$$

As the dimension of the data increases, the chain rule is harder to compute. In fact, many models try to simplify it in some ways.

Why we need probabilistic graphical models

Reasons:

• They provide a simple way to visualize the structure of a probabilistic model and can be used to design and motivate new models.

• Insights into the properties of the model, including conditional independence properties, can be obtained by inspection of the graph.

• Complex computations, required to perform inference and learning in sophisticated models, can be expressed in terms of graphical manipulations, in which underlying mathematical expressions are carried along implicitly.

Three major parts of PGM

• Representation: Express a probability distribution that models some real-world phenomenon.

• Inference: Obtain answers to relevant questions from our models.

• Learning: Fit a model to real-world data.

We are going to mainly focus on Representation in this post.

Representation

Representation: Express a probability distribution that models some real-world phenomenon.

Directed graphical models (Bayesian networks)

Directed graphical models is also known as Bayesian networks.

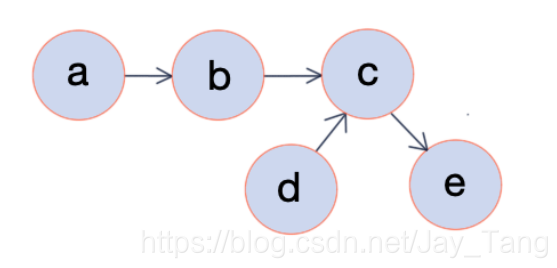
Intuition:

In a directed graph, vertices correspond to variables x i x_i x