往期文章链接目录
文章目录
Jensen’s inequality
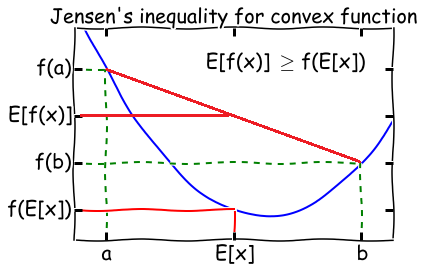
- Theorem: Let f f f be a convex function, and let X X X be a random variable. Then:
E [ f ( X ) ] ≥ f ( E [ X ] ) E[f(X)] \geq f(E[X]) E[f(X)]≥f(E[X])
\quad Moreover, if f f f is strictly convex, then E [ f ( X ) ] = f ( E [ X ] ) E[f(X)] = f(E[X]) E[f(X)]=f(E[X]) holds true if and
only if X X X is a constant.
- Later in the post we are going to use the following fact from the Jensen’s inequality:
Suppose λ j ≥ 0 \lambda_j \geq 0 λj≥0 for all j j j and ∑ j λ j = 1 \sum_j \lambda_j = 1 ∑jλj=1, then
log ∑ j λ j y j ≥ ∑ j λ j l o g y j \log \sum_j \lambda_j y_j \geq \sum_j \lambda_j \, log \, y_j logj∑λjyj≥j∑λjlogyj
\quad where the log \log log function is concave.
Overview of Expectation–Maximization (EM) algorithm
In this post, let Y Y Y be a set of observed data, Z Z Z a set of unobserved latent data, and θ \theta θ the unknown parameters.
(After this post, you will be comfortable with the following description about the EM algorithm.)
Expectation–Maximization (EM) algorithm is an iterative method to find (local) maximum likelihood estimation (MLE) of L ( θ ) = p ( Y ∣ θ ) L(\theta) = p(Y|\theta) L(θ)=p(Y∣θ), where the model depends on unobserved latent variables Z Z Z.
Algorithm:
- Initialize peremeters θ 0 \theta_0 θ0.
Iterate between steps 2 and 3 until convergence:
- an expectation (E) step, which creates a function Q ( θ , θ i ) Q(\theta, \theta_i) Q(θ,θi) for the expectation of the log-likelihood log p ( Y , Z ∣ θ ) \log p(Y,Z|\theta) logp(Y,Z∣θ) evaluated using the current conditional distribution of
Z Z Z given Y Y Y and the current estimate of the parameters θ i \theta_i θi, where
Q ( θ , θ i ) = ∑ Z P ( Z ∣ Y , θ i ) ⋅ log p ( Y , Z ∣ θ ) = E Z ∼ P ( Z ∣ Y , θ i ) [ log p ( Y , Z ∣ θ ) ] \begin{aligned} Q(\theta, \theta_i) &= \sum_Z P(Z|Y,\theta_i) \cdot \log p(Y,Z|\theta) \\ &= E_{Z \sim P(Z|Y,\theta_i)}[\log p(Y,Z|\theta)] \end{aligned} Q(θ,θi)=Z∑P(Z∣Y,θi)⋅logp(Y,Z∣θ)=EZ∼P(Z∣Y,θi)[logp(Y,Z∣θ)]
- A maximization (M) step, which computes parameters maximizing the expected log-likelihood Q ( θ , θ i ) Q(\theta, \theta_i) Q(θ,θi) found on the E E E step and then update parameters to θ i + 1 \theta_{i+1} θi+1.
These parameter-estimates are then used to determine the distribution of the latent variables in the next E E E step. We say it converges if the increase in successive iterations is smaller than some tolerance parameter.
In general, multiple maxima may occur, with no guarantee that the global maximum will be found.
Intuition: Why we need EM algorithm
Sometimes maximizing the likelihood ℓ ( θ ) \ell(\theta) ℓ(θ) explicitly might be difficult since there are some unknown latent variables. In such a setting, the EM algorithm gives an efficient method for maximum likelihood estimation.
Complete Case v.s. Incomplete Case
Complete case
( Y , Z ) (Y, Z) (Y,Z) is observable, and the log likelihood can be written as
ℓ ( θ ) = log p ( Y , Z ∣ θ ) = log p ( Z ∣ θ ) ⋅ p ( Y ∣ Z , θ ) = log p ( Z ∣ θ ) + log p ( Y ∣ Z , θ ) \begin{aligned} \ell(\theta) &= \log p(Y, Z | \theta) \\ &= \log p(Z|\theta) \cdot p(Y|Z, \theta) \\ &= \log p(Z|\theta) + \log p(Y|Z, \theta) \\ \end{aligned} ℓ(θ)=logp(Y,Z∣θ)=logp(Z∣θ)⋅p(Y∣Z,θ)=logp(Z∣θ)+logp(Y∣Z,θ)
We subdivide our task of maximizing ℓ ( θ ) \ell(\theta) ℓ(θ) into two sub-tasks. Note that in both log p ( Z ∣ θ ) \log p(Z|\theta) logp(Z∣θ) and log p ( Y ∣ Z , θ ) \log p(Y|Z, \theta) logp(Y∣Z,θ), the only unknown parameter is θ \theta θ. They are just two standard MLE problems which could be easily solved by methods such as gradient descent.
Incomplete case
( Y ) (Y) (Y) is observable, but ( Z ) (Z) (Z) is unknown. We need to introduce the marginal distribution of variable Z Z Z:
ℓ ( θ ) = log p ( Y ∣ θ ) = log ∑ Z p ( Y , Z ∣ θ ) = log ∑ Z p ( Z ∣ θ ) ⋅ p ( Y ∣ Z , θ ) \begin{aligned} \ell(\theta) &= \log p(Y | \theta) \\ &= \log \sum_Z p(Y, Z | \theta) \\ &= \log \sum_Z p(Z|\theta) \cdot p(Y|Z, \theta) \\ \end{aligned} ℓ(θ)=logp(Y∣θ)=logZ∑p(Y,Z∣θ)=logZ∑p(Z∣θ)⋅p(Y∣Z,θ)
Here we have a summation inside the log, so it’s hard to use optimization methods or take derivatives. This is the case where EM algorithm comes into aid.
EM Algorithm Derivation (Using MLE)
Given the observed data Y Y Y, we want to maximize the likelihood ℓ ( θ ) = p ( Y ∣ θ ) \ell(\theta) = p(Y|\theta) ℓ(θ)=p(Y∣θ), and it’s the same as maximizing the log-likelihood log p ( Y ∣ θ ) \log p(Y|\theta) logp(Y∣θ). Therefore, from now on we will try to maximize the likelihood
ℓ ( θ ) = log p ( Y ∣ θ ) \ell(\theta) = \log p(Y|\theta) ℓ(θ)=logp(Y∣θ)
by taking the unknown variable Z Z Z into account, we rewrite the objective function as
ℓ ( θ ) = log p ( Y ∣ θ ) = log ∑ Z p ( Y , Z ∣ θ ) = log ∑ Z p ( Y ∣ Z , θ ) ⋅ p ( Z ∣ θ ) \begin{aligned} \ell(\theta) &= \log p(Y|\theta) \\ &= \log \sum_Z p(Y, Z | \theta) \\ &= \log \sum_Z p(Y|Z,\theta) \cdot p(Z|\theta) \\ \end{aligned} ℓ(θ)=logp(Y∣θ)=logZ∑p(Y,Z∣θ)=logZ∑p(Y∣Z,θ)⋅p(Z∣θ)
Note that in the last step, the log \log log is outside of the ∑ \sum ∑, which is hard to compute and optimize. Check out my previous post to know why we prefer to have log \log log inside of ∑ \sum ∑, instead of outside. So later we would find a way to approximate it (Jensen’s inequality).
Suppose we follow the iteration step 2 (E) and 3 (M) repeatedly, and have updated parameters to θ i \theta_i θi, then the difference between ℓ ( θ ) \ell(\theta) ℓ(θ) and our estimate ℓ ( θ i ) \ell(\theta_i) ℓ(θi) is ℓ ( θ ) − ℓ ( θ i ) \ell(\theta) - \ell(\theta_i) ℓ(θ)−ℓ(θi). You can think of this difference as the improvement that later estimate of θ \theta θ tries to achieve. So our next step is to find θ i + 1 \theta_{i+1} θi








 EM算法是一种迭代方法,用于在存在未观察到的潜在变量的情况下进行最大似然估计。本文介绍了EM算法的背景,通过Jensen's不等式解释其必要性,并详细推导了算法过程,包括E步和M步。此外,还探讨了算法的收敛性和在K-means和GMM中的应用。
EM算法是一种迭代方法,用于在存在未观察到的潜在变量的情况下进行最大似然估计。本文介绍了EM算法的背景,通过Jensen's不等式解释其必要性,并详细推导了算法过程,包括E步和M步。此外,还探讨了算法的收敛性和在K-means和GMM中的应用。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 1720
1720

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








