02笔记离散数学——命题逻辑——基于离散数学(第3版)_章炯民,陶增乐

原创已于 2025-01-24 16:40:21 修改 · 1.6k 阅读

5 ·

CC 4.0 BY-SA版权

文章标签：

#离散数学

于 2021-09-18 11:34:26 首次发布

离散数学专栏收录该内容

9 篇文章

订阅专栏

本文深入讲解了命题逻辑的基础概念，包括命题、逻辑联结词及其运算规则，并介绍了真值表、命题公式的类型及等值演算等内容。此外，还探讨了范式、真值函数及推理系统的相关理论。

命题逻辑

命题和逻辑联结

确定真假的陈述句称为命题
用1表示真 0表示负

当命题不能进一步拆分成更简单的命题，称为原子命题，其他命题称为复合命题。

联结词

否定联结词：
$⌝\urcorner$
非p，对p的否定

合取联结词：
$∧\land$
p并且q

析取联结词：
$∨\lor$
p或者q

蕴涵联结词
$→\to$
如果p，那么q。p蕴含q
善意规定：如果p是0，默认p->q是真的

等价联结词
$↔\leftrightarrow$
p当且仅当q，p与q等价

真值表在这里插入图片描述

命题公式

命题变量：表示某个命题的变量
命题常量：命题公式中的常量

n元命题公式：含有n个命题变量的命题公式
子公式：B是A公式的一部分，那么B是子公式

规定运算优先级
$⌝∧∨→↔\urcorner \quad \land \quad \lor \quad \to \quad \leftrightarrow$

命题公式类型
①重言式（永真式）
②矛盾式（永假式）
③可满足式：有成真赋值

1）p-> p or q永真
2) p and not p 永假
3） p->q->r 可满足式

等值演算

方法一：证明两个命题等值可以用真值表
$\land q) \lor r = (p\lor r) \land(q\lor r)$
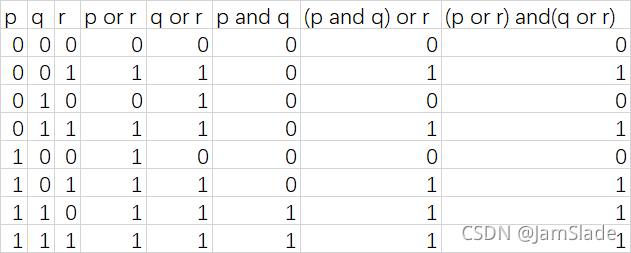
在这里插入图片描述

恒等式
1）双重否定
$⌝⌝A⇔A\urcorner \urcorner A \Leftrightarrow A$
2)幂等律
$A∧A⇔AA∨A⇔AA\land A\Leftrightarrow A \quad A\lor A \Leftrightarrow A$
3)交换律
$A∧B⇔B∧AA∨B⇔B∨AA\land B \Leftrightarrow B\land A \quad A\lor B \Leftrightarrow B\lor A$
4)结合律
$(A∧B)∧C⇔A∧(B∧C)(A∨B)∨C⇔A∨(B∨C)(A\land B)\land C \Leftrightarrow A\land(B\land C) \quad (A\lor B)\lor C \Leftrightarrow A\lor(B\lor C)$
5)分配律
$(A∧B)∨C⇔(A∨C)∧(B∨C)(A∨B)∧C⇔(A∧C)∨(B∧C)(A\land B)\lor C \Leftrightarrow (A\lor C)\land(B\lor C) \\(A\lor B)\land C \Leftrightarrow (A\land C)\lor(B\land C)$

6)德摩根律
$⌝(A∧B)⇔(⌝A∨⌝B)⌝(A∨B)⇔(⌝A∧⌝B)\urcorner(A\land B) \Leftrightarrow (\urcorner A \lor \urcorner B) \\ \urcorner(A\lor B) \Leftrightarrow (\urcorner A \land \urcorner B)$
7)吸收率
$A∨(A∧B)⇔AA∧(A∨B)⇔AA\lor(A\land B) \Leftrightarrow A \quad A\land(A\lor B) \Leftrightarrow A$
8)零律
$A∧0⇔AA∨1⇔1A\land 0 \Leftrightarrow A \quad A\lor 1 \Leftrightarrow 1$
9)同一律
$A∨0⇔AA∧1⇔AA\lor 0 \Leftrightarrow A\quad A\land 1 \Leftrightarrow A$
10)
$A∨⌝A⇔1A∧⌝A⇔0A\lor \urcorner A \Leftrightarrow 1 \\ A\land \urcorner A\Leftrightarrow 0$
11)蕴含等式
$A→B⇔⌝A∨BA\to B \Leftrightarrow \urcorner A \lor B$
12）假言易位式
$A→B⇔⌝B→⌝AA\to B \Leftrightarrow \urcorner B \to \urcorner A$
13)等价恒等式
$A↔B⇔(A→B)∧(B→A)A\leftrightarrow B \Leftrightarrow (A\to B) \land(B\to A)$
对偶原理
将A中的and or 0 1换成 or and 1 0，就是对偶式，记为A*

范式

文字：命题变量或它的否定形式
$p⌝pp\quad \urcorner p$
主析取范式：极小项的析取式，和原命题公式等值
极小项：文字的合取式，每个命题变量仅出现一次
编号：按二进制
极小项编码二进制串对应唯一成真赋值

主合取范式：极大项得和去向
极大项取唯一成假赋值
主合取范式和主析取范式取凡是对称

n元真值函数
$F(a_1……a_n)$
设S是一个联结词的集合，对于任何n元真值函数F（x1……xn)，都存在仅含S中的联结词的命题公式A，A所对应的联结词的命题公式A，A所对应的真值函数恰为F，则称改联结词S是完备的或完备集，完备的集合任何真子集均不是完备的，则该联结词极小完备的

冗余联结词：
独立联结词：
极小完备集：

推理系统

定义1

H1……Hn,C都是命题公式，若（H1 and …… and Hn）-> C是重言式
称H1……Hn推出结论C的推理正确或有效
H1……Hn称为C的前提
C是H1……Hn的有效结论
记为（H1……Hn) => C

定义2
从前提集合{H1……Hn}出发，得到一个公式序列S1……Sm
1）Sm恰为C
2）任意i＜m，Si要么是前提，要么是前面公式推理得出

自然推理规则
P规则：前提引入规则
T规则：重言蕴含规则

派生
1）置换规则
$A⇔B，则A推出BA\Leftrightarrow B，则A推出B$
2）假言推理
$A和A→B,推出BA和A\rightarrow B,推出B$
3）附加
$A推出A∨BA推出A\lor B$
4）化简
$A∧B推出AA\land B推出A$
5）拒取式
$¬B和A→B推出¬A\lnot B和A\rightarrow B 推出\lnot A$
6）假言三段论
$A→B和B→C推出A→CA\rightarrow B 和 B\rightarrow C推出A\rightarrow C$
7）析取三段论
$¬B和A∨B推出A\lnot B和A\lor B 推出 A$
8）构造性二难推理
$A∧C、A→B和C→D推出A\land C、A\rightarrow B和C\rightarrow D推出$
9）破坏性二难推理
$¬B∧¬D、A→B和C→D推出¬A∨¬C\lnot B\land \lnot D、A\rightarrow B 和 C\rightarrow D 推出 \lnot A \lor \lnot C$
10）合取引入
$A和B推出A∧BA和B推出A\land B$