二叉排序树，平衡二叉树和哈夫曼树

1. 二叉排序树查找

//递归
BiTNode *BST_Search_R(BiTree biTree, ElemType key) {
    if (biTree == NULL || key == biTree->data) return biTree;
    if (key < biTree->data) return BST_Search_R(biTree->lChild, key);
    else return BST_Search_R(biTree->rChild, key);
}

//非递归
BiTNode *BST_Search(BiTree biTree, ElemType key) {
    while (biTree != NULL && key != biTree->data){
        if (key<biTree->data) biTree = biTree->lChild;
        else biTree = biTree->rChild;
    }
    return biTree;
}

2. 二叉排序树插入

//二叉排序树插入
int BST_Insert(BiTree &biTree, ElemType key) {
    if (biTree == NULL) {
        biTree = (BiTree) malloc(sizeof(BiTNode));
        biTree->data = key;
        biTree->lChild = biTree->rChild = NULL;
        return 1;
    } else if (key==biTree->data) {
        return 0;
    } else if (key < biTree->data){
        return BST_Insert(biTree->lChild,key);
    } else{
        return BST_Insert(biTree->rChild,key);
    }
}

3. 二叉排序树构造

//二叉排序树构造
void create_BST(BiTree &biTree, ElemType array[], int n) {
    biTree = NULL;
    int i = 0;
    while (i < n) {
        BST_Insert(biTree, array[i]);
        i++;
    }
}

4. 二叉排序树的删除
   1) 删除叶子结点
   2)删除结点只有一颗左子树或右子树
   3)删除结点右左右子树
   

•   后继：右子树最左的结点（最小值）
    前驱：左子树最右的结点（最大值）
    注：为什么要上面这样？
    因为要维持二叉排序树的性质：左子树结点的值 < 根结点的值 < 右子树结点		
  

5. 二叉排序树的查找效率分析
   
   

---

1. 二叉平衡树结构

//二叉平衡树结构
typedef struct AVLNode {
    int data;//数据域
    int balance;//平衡因子
    AVLNode *lChild, *rChild;
} AVLNode, *AVLTree;

2. 平衡二叉树插入

只需调整最小不平衡子树


1）LL：右旋


2）RR：左旋

3）LR：先左旋后右旋

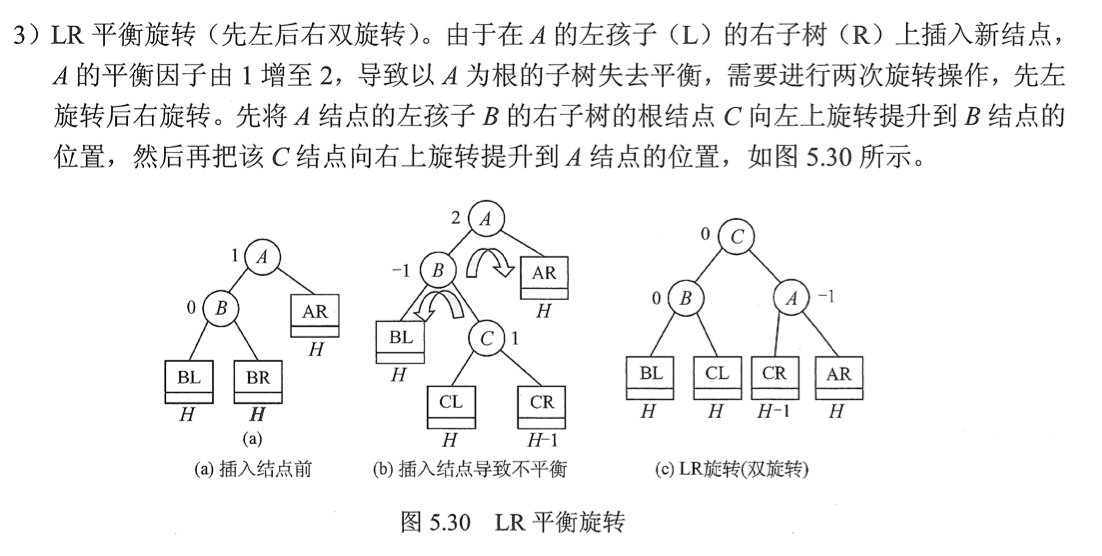
4）RL：先右旋后左旋

含有n个结点的平衡二叉树的最大深度为O(log2n)，即平均查找长度为O(log2n)

---

1. 哈夫曼树的构造（P180）
   抽取最小的两个结点，将它们的权值相加成它俩的父节点，后续重复此动作，可得到最小权值的哈夫曼树

2. 哈夫曼编码