具有n个结点的完全二叉树的深度_树与二叉树

树的基本概念

1. 树：包括n（n>=0)个节点的有穷集合T，任意非空树T满足以下条件：

• 有且仅有一个特定的称为根的结点；
• 除根结点之外，其余结点分成若干个互不相交的有限集合，这些集合中的每一个又都是树，称为根的字树

1. 树的专业名词：

• 双亲结点
• 孩子结点
• 兄弟结点
• 祖先结点
• 子孙结点
• 结点层次：根为第一层；
• 树的高度（深度）
• 堂兄结点

1. 有序树：将树中结点的各子树看成从左向右次序的（次序不能互换）；
2. 无序树:结点之间没有次序，课互换位置；
3. 结点的次序：在有序树中可以从左到右规定结点的次数；
4. 长子：在有序树中，把一个结点最左边得子结点称为长子；
5. 森林：m课互不相交得树得集合；

二叉树

1. 定义：每个结点最多有两棵子树（不存在度大于2的结点）并且二叉树的子树有左右之分，不能任意颠倒顺序；
2. 满二叉树：每层结点都为满的二叉树（即每层结点都具有最大结点数）；
3. 完全二叉树：只有最下面两层结点度数小于2，其余各层结点度数都等于2，并且最下面一层的结点都应该集中在该层最左边的若干上；
4. 二叉树的主要性质

• 在非空二叉树的第h层上，至多有
  个结点（h>=1);
• 深度为k(k>=1)的二叉树，最多有
  个结点；
• 对于任意一棵非空的树二叉树，如果叶子结点个数为
  ，度数为2的结点个数为
  ,则
  =
  +1;
• 具有n个结点的完全二叉树的高度k为[
  ]+1

二叉树的存储——顺序存储和链式存储

1. 顺序存储：采用一组地址连续的存储单元依次自上而下、自左至右存储完全二叉树上的结点元素；
2. 链式存储：使用指针域链接各个结点；

完全二叉树的顺序存储：按照从上到下，从左到右的顺序对二叉树所有结点编号后存储；

一般二叉树的顺序存储：将各个结点与完全二叉树上的结点相对照，并存储在一维数组的相应位置上，用‘0’或者^表示不存在的结点；

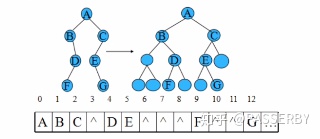
二叉树的链式存储：

二叉链表法：

二叉链表法

typedef struct bitnode
{
    int data;
    struct bitnode *lchild,*rchild;
}bitnode,*bitnode;

三叉链表法

typedef struct bitnode
{
    int data;
    struct bitnode *lchild,*rchild，*parent;
}bitnode,*bitnode;

二叉树的遍历：按某条搜索路径寻访树中的每个结点，使得每个结点均被访问一次，而且仅被访问一次；

二叉树的组成：根结点、左子树和右子树；

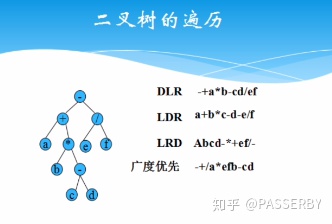
遍历的类别：深度优先遍历和广度优先遍历

DLR（先根次序）：根、左子树，右子树

LDR（中根次序）：左子树、根、右子树

LRD（后根次序）：左子树，右子树、根

代码的实现：


#include<stdio.h>
#include<stdlib.h>
 
typedef struct node{
 	int data;
 	struct node* left;
 	struct node* right;
 }Node;
 
 void preorder(Node* node)
 {
 	if(node != NULL)
 	{
 		printf("%d  ",node->data);
 		preorder(node->left);
 		preorder(node->right);
	 }
	 
 }
 void inorder(Node* node)
 {
 	if(node != NULL)
 	{
 		inorder(node->left);
 		printf("%d  ",node->data);
 		inorder(node->right);
	 }
	 
 }
 void posorder(Node* node)
 {
 	if(node != NULL)
 	{
 		inorder(node->right);
 		printf("%d  ",node->data);
 		inorder(node->left);
	 }
	 
 }
 int main()
 {
 	Node n1,n2,n3,n4;
 	
 	n1.data=5;
 	n2.data=6;
 	n3.data=7;
 	n4.data=8;
 	
 	n1.left=&n2;
 	n1.right=&n3;
 	n2.left=&n4;
 	n2.right=NULL;
 	n3.left=NULL;
 	n3.right=NULL;
 	n4.left=NULL;
 	n4.right=NULL;
 	
 	printf("前序遍历n");
 	preorder(&n1);
 	printf("n");
 	printf("中序遍历n");
 	inorder(&n1);
 	printf("n");
 	printf("后序遍历n");
 	posorder(&n1);
 }

#include<stdio.h>
#include<stdlib.h>

typedef struct node 
{
	int data;
	struct node * left;
	struct node * right;
 } Node;
 
 typedef struct
 {
 	Node* root;
 }Tree;
 void preorder(Node* node)
 {
 	if(node != NULL)
 	{
 		printf("%d  ",node->data);
 		preorder(node->left);
 		preorder(node->right);
	 }
	 
 }
 void inorder(Node* node)
 {
 	if(node != NULL)
 	{
 		inorder(node->left);
 		printf("%d  ",node->data);
 		inorder(node->right);
	 }
	 
 }
 void posorder(Node* node)
 {
 	if(node != NULL)
 	{
 		inorder(node->right);
 		printf("%d  ",node->data);
 		inorder(node->left);
	 }
	 
 }
 void insert(Tree* tree, int value)
 {
 	Node* node = (Node*)malloc(sizeof(Node));
 	node->data = value;
 	node->left=NULL;
 	node->right=NULL;
 	
 	if(tree->root==NULL)
 	{
 		tree->root=node;
	}
	 else
	{
	 		Node *temp =tree->root;
			while(temp != NULL)
			{
				if(value<temp->data)
				{
					if(temp->left==NULL)
					{
						temp->left=node;
						return ;
					}
					else
					{
						temp=temp->left;
					}
				}
				else
				{
				if(temp->right==NULL)
					{
						temp->right=node;
						return ;
					}
					else
					{
						temp=temp->right;
					}
				}
			 } 
		}
	}
	
	int main()
	{
		int a[7]={6,3,8,2,5,1,7};
		Tree tree;
		tree.root = NULL;
		
		int i;
		for(i=0;i<7;i++)
		{
			insert(&tree,a[i]);	
		}
		 
	 	printf("前序遍历n");
	 	preorder(tree.root);
	 	printf("n");
	 	printf("中序遍历n");
	 	inorder(tree.root);
	 	printf("n");
	 	printf("后序遍历n");
	 	posorder(tree.root);
 }