1、BST
先介绍一下BST二叉搜索树(Binary Search Tree)。对于二叉搜索树的每个节点,其左节点的值小于等于它,右节点的值大于它。如图1所示
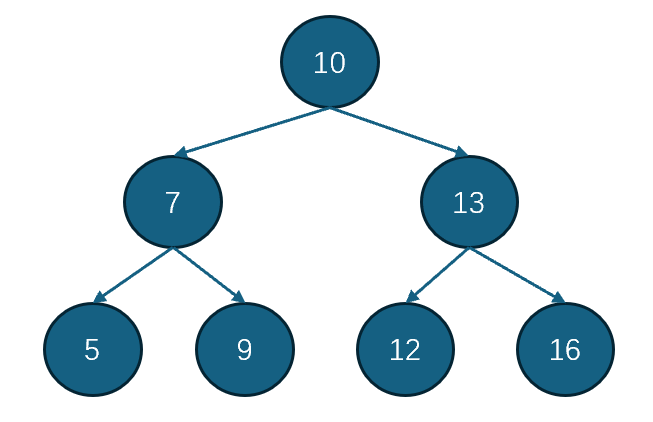
为后续描述方便,定义几个概念:根节点、叶子节点、左子树、右子树、左节点、右节点、父节点。如图1中,10节点为整个搜索树的根节点;5、9、12、16为叶子节点;7、13分别为10的左节点和右节点。5、7、9组成的子树为10的左子树;12、13、16节点组成的子树为10的右子树。10为7、13的父节点;7为6、9的父节点;13为12、16的父节点
树结构有三种操作:搜索、插入、删除。
1.1 搜索
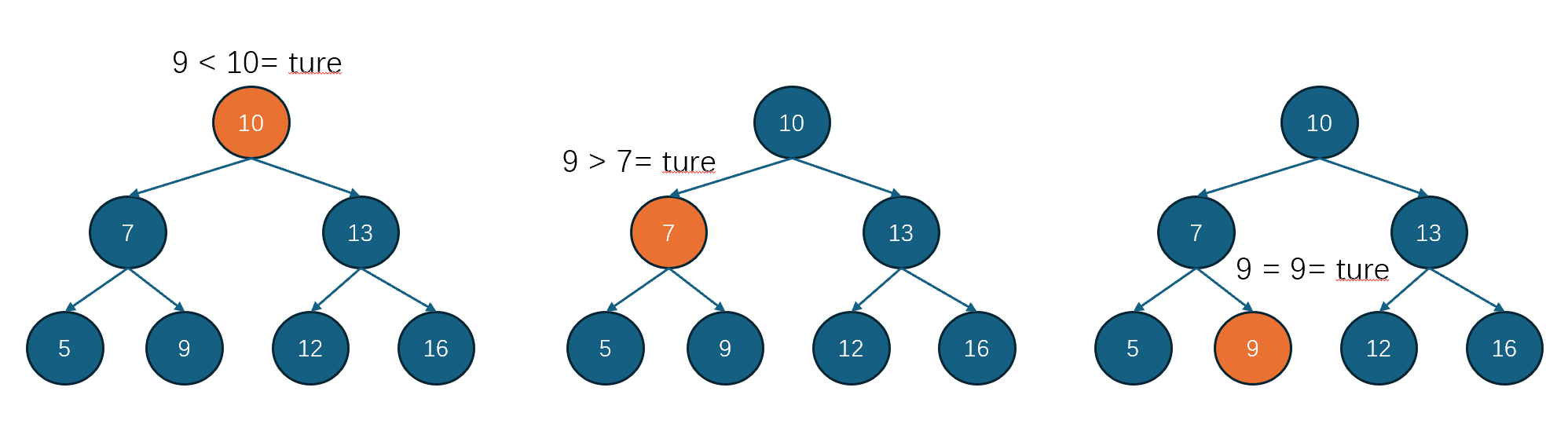
搜索:BST搜索操作时间复杂度为O(logn),如图1中需要搜索节点9。那从根节点出发,9小于根节点10,那么9如果存在则必然在10的左子树。再判断9大于 10的左节点7,那么9如果存在则必然在7的右子树。再判断7的右节点就是等于9,即只花了三步就在7个元素中找到了9节点。
1.2 插入
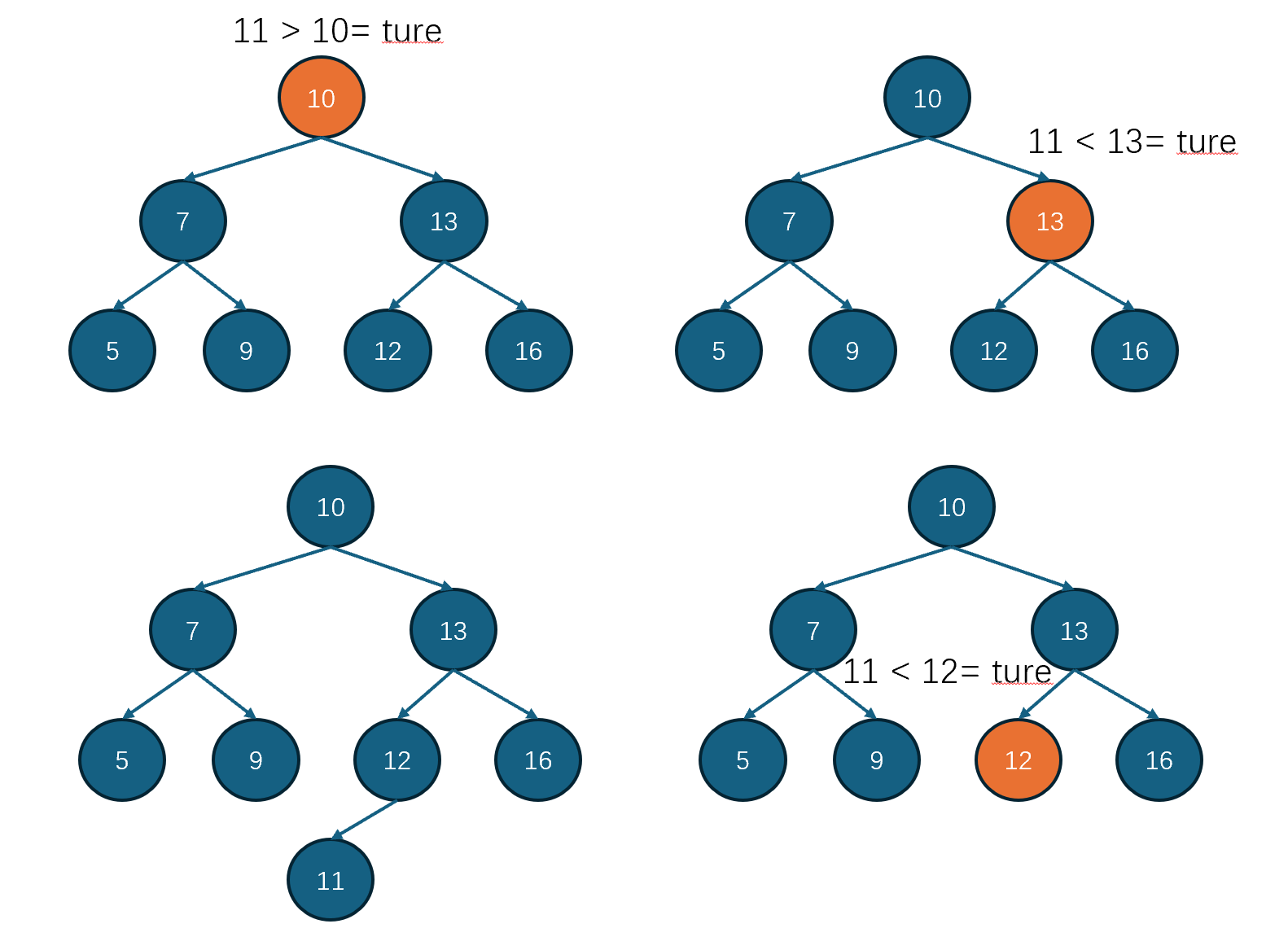
插入:BST新插入的节点,永远在叶子节点。这个应该很好理解,如图所以,如果还需要插入值为11的节点,那需要从根节点出发,11大于根节点10,所以11应该插入在根节点的右侧。再判断11小于10节点的右节点13,所以11节点应该插入在13节点的左侧。
1.3 删除
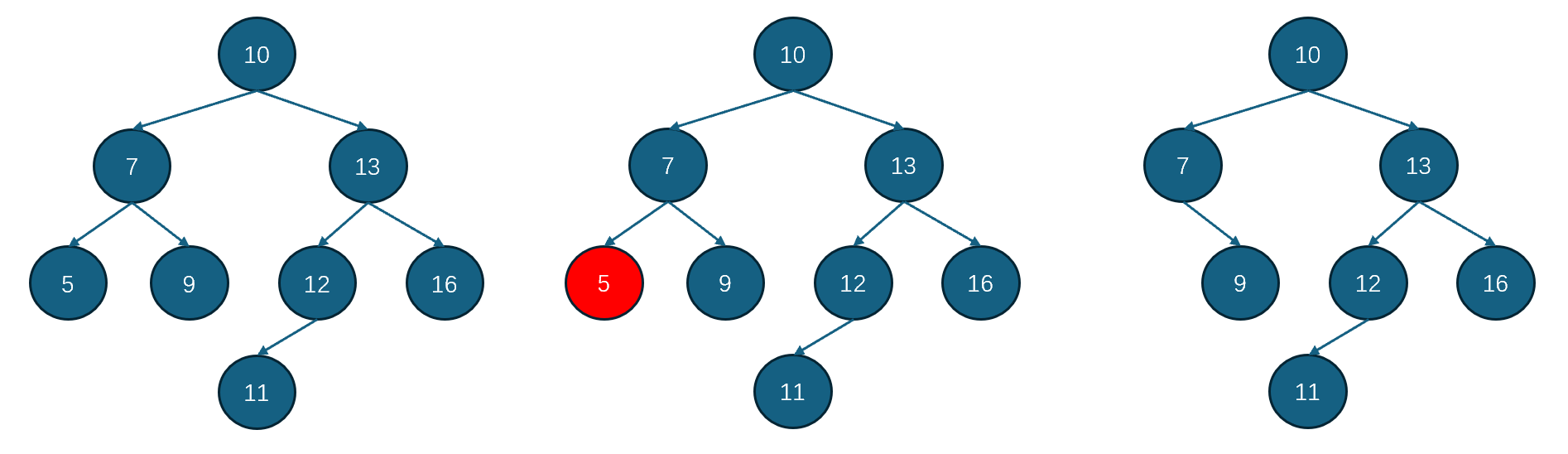
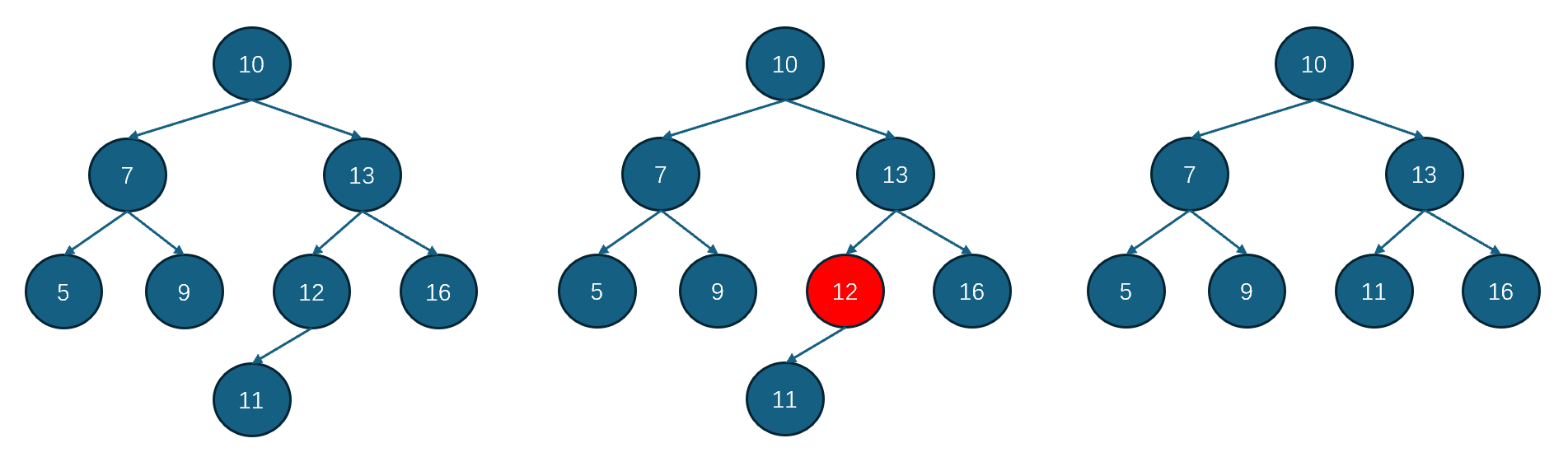
删除:删除操作比插入和搜索要稍微复杂一些,一共分为三种情况。首先介绍最简单的一种:删除叶子节点。如上图中的BST,需要删除5节点,那先要查询是否存在5,然后判断是否为叶子节点,然后直接删除,如下图所示:
第二种情况为:删除的节点的左右子树仅一侧存在(即左子树存在,右子树为空;或左子树为空,右子树存在)。比如删除节点12(左子树存在,右子树为空),那么还是先搜索12节点,那么将12节点的左子树与12节点的父节点直接相连。相当于12的左子树直接代替12。
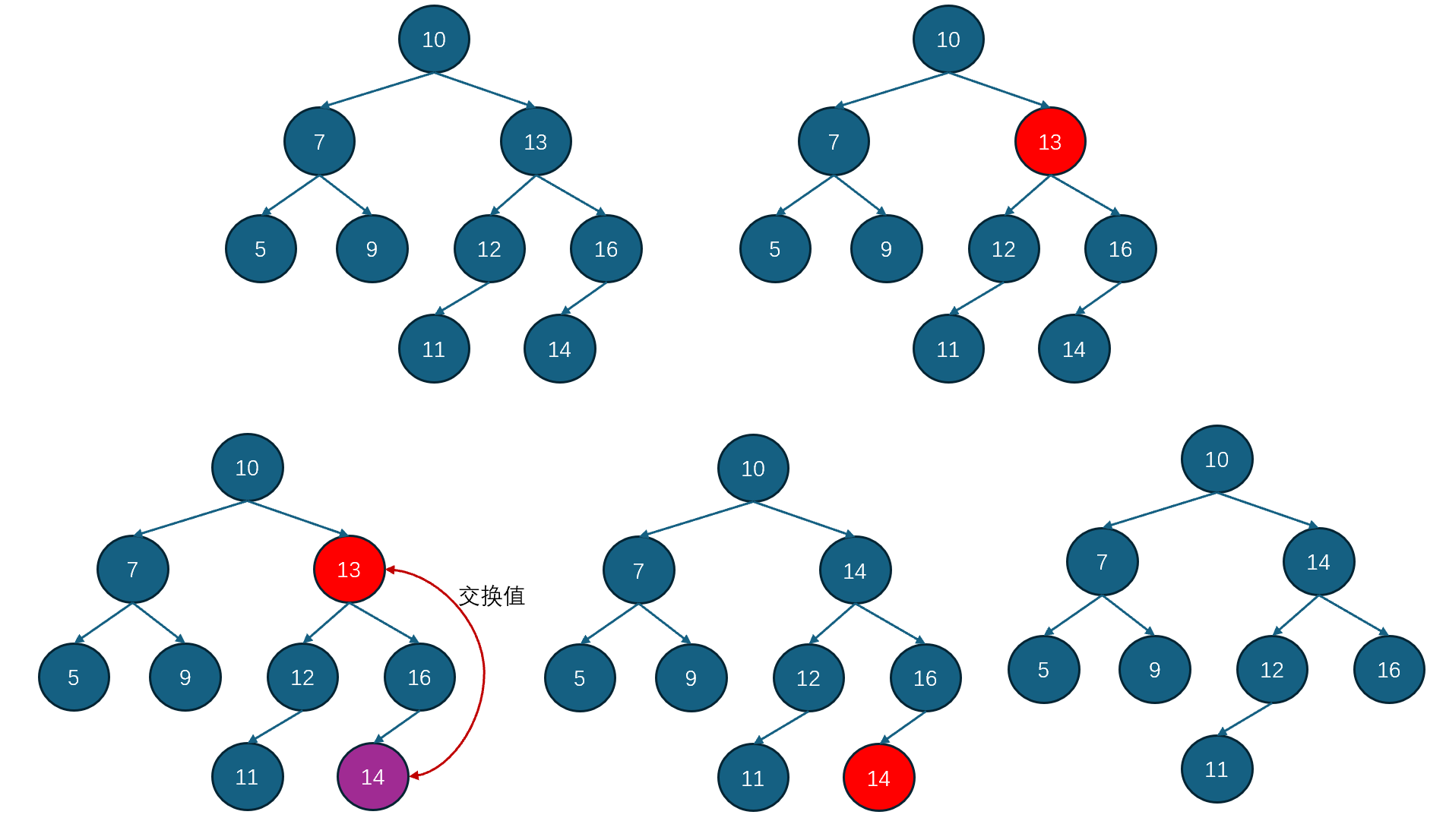
第三种情况为:删除的节点左右子树均存在。如图所示,需要删除节点13。如果直接删除13,不好处理13左右子树与13父节点的连接关系。可以找到13右子树的最小值,然后取代13,然后再删除被替换的叶子节点,这个问题就很解决了,如下图所示。(当前也可以去找左子树的最大值。我代码中是用的右子树的最小值,我就用这种情况举例了)
1.4 代码
接下来直接撸BST的完整代码,首先定义了一个基类BaseNode<T>(后续写AVL也会用到),定义了一些常用的方法,比如插入左右节点,判断是否为根节点、叶子节点等;Result类是个人开发习惯喜欢用的一个类,标准化模块间的输入输出;:
///接口
internal interface IOperation
{
void Insert(int value);
Result Query(int value);
Result Delete(int value);
}
/// <summary>
/// 标准返回
/// </summary>
public class Result
{
/// <summary>
/// 返回状态
/// </summary>
public bool Status { get; set; }
/// <summary>
/// 具体信息
/// </summary>
public string Message { get; set; }
}
/// <summary>
/// 标准返回带数据
/// </summary>
/// <typeparam name="T"></typeparam>
public class Result<T> : Result
{
public T Data { get; set; }
}
///节点基类
public class BaseNode<T> where T: BaseNode<T>
{
/// <summary>
/// 值
/// </summary>
private int _value;
/// <summary>
/// 坐节点
/// </summary>
private T _leftNode = default(T);
/// <summary>
/// 右节点
/// </summary>
private T _rightNode = default(T);
/// <summary>
/// 父节点
/// </summary>
private T _parentNode = default(T);
public int Value { get => _value; }
public T RightNode { get => _rightNode; }
public T LeftNode { get => _leftNode; }
public T ParentNode { get => _parentNode; }
public bool IsRoot { get => _parentNode == null; }
public bool HaveLeftNode { get => _leftNode != null; }
public bool HaveRightNode { get => _rightNode != null; }
public bool IsLeftNode { get => _parentNode != null && _parentNode._leftNode == this; }
public bool IsRightNode { get => _parentNode != null && _parentNode._rightNode == this; }
public bool IsLeaf { get => _rightNode == null && _leftNode == null; }
public bool HasBothNode { get => _rightNode != null && _leftNode != null; }
public BaseNode(int value)
{
_value = value;
}
/// <summary>
/// 修改值
/// </summary>
/// <param name="value"></param>
public void ChangeValue(int value)
{
_value = value;
}
/// <summary>
/// 插入左节点
/// </summary>
/// <param name="node"></param>
public void InsertLeft(T node)
{
_leftNode = node;
if (node != null)
{
node.AddParent(this as T);
}
}
/// <summary>
/// 插入右节点
/// </summary>
/// <param name="node"></param>
public void InsertRight(T node)
{
_rightNode = node;
if (node != null)
{
node.AddParent(this as T);
}
}
/// <summary>
/// 添加父节点
/// </summary>
/// <param name="node"></param>
private void AddParent(T node)
{
_parentNode = node;
}
}
//BST 节点类
public class BSTNode : BaseNode<BSTNode>
{
public BSTNode(int value) : base(value) { }
}
BaseTree是一个树的基类,BSTree是BST的完整实现
public class BaseTree<T>
{
public T Root { get => _root; }
internal T _root = default(T);
}
public class BSTree: BaseTree<BSTNode>, IOperation
{
public BSTree(int val)
{
_root = new BSTNode(val);
}
#region 对外接口
/// <summary>
/// 插入
/// </summary>
/// <param name="val"></param>
public void Insert(int val)
{
if(_root == null)
{
_root = new BSTNode(val);
}
else
{
Insert(_root, val);
}
}
/// <summary>
/// 查询
/// </summary>
/// <param name="val"></param>
/// <returns></returns>
public Result Query(int value)
{
Result result = new Result();
if(Query(_root, value) == null)
{
result.Status = false;
result.Message = "No Such Node!";
}
else
{
result.Status = true;
}
return result;
}
/// <summary>
/// 删除
/// </summary>
/// <param name="val"></param>
/// <returns></returns>
public Result Delete(int value)
{
Result result = new Result() { Status = true };
BSTNode deleteNode = Query(_root, value);
if(deleteNode == null)
{
result.Status = false;
result.Message = "No such Node!";
}
if (deleteNode.IsRoot)
{
DeleteLeafNode(deleteNode);
}
else if (deleteNode.HasBothNode)
{
BSTNode exchangeNode = deleteNode.RightNode;
while (exchangeNode.LeftNode != null)
{
exchangeNode = exchangeNode.LeftNode;
}
deleteNode.ChangeValue(exchangeNode.Value);
if (deleteNode.IsLeaf)
{
DeleteLeafNode(exchangeNode);
}
else
{
DeleteNodeOnlyRightChild(exchangeNode);
}
}
else if (deleteNode.HaveLeftNode)
{
DeleteNodeOnlyLeftChild(deleteNode);
}
else if (deleteNode.HaveRightNode)
{
DeleteNodeOnlyRightChild(deleteNode);
}
else
{
result.Status = false;
result.Message = "System Error!";
}
return result;
}
#endregion
/// <summary>
/// 插入
/// </summary>
/// <param name="curNode"></param>
/// <param name="val"></param>
private void Insert(BaseNode<BSTNode> curNode, int value)
{
if (value <= curNode.Value)
{
if (curNode.HaveLeftNode)
{
Insert(curNode.LeftNode, value);
}
else
{
curNode.InsertLeft(new BSTNode(value));
}
}
else
{
if (curNode.HaveRightNode)
{
Insert(curNode.RightNode, value);
}
else
{
curNode.InsertRight(new BSTNode(value));
}
}
}
/// <summary>
/// 删除
/// </summary>
/// <param name="node"></param>
/// <param name="val"></param>
/// <returns></returns>
private BSTNode Query(BSTNode node, int value)
{
if(node.Value == value)
{
return node;
}
if (value > node.Value)
{
if (node.HaveRightNode)
{
return Query(node.RightNode, value);
}
else
{
return null;
}
}
else
{
if (node.HaveLeftNode)
{
return Query(node.LeftNode, value);
}
else
{
return null;
}
}
}
/// <summary>
/// 删除叶子节点
/// </summary>
/// <param name="node"></param>
private void DeleteLeafNode(BSTNode deleteNode)
{
if (deleteNode.IsRoot)
{
_root = null;
}
else
{
if (deleteNode.IsLeftNode)
{
deleteNode.ParentNode.InsertLeft(null);
return;
}
if (deleteNode.IsRightNode)
{
deleteNode.ParentNode.InsertRight(null);
}
}
}
/// <summary>
/// 删除只有左子树的节点
/// </summary>
private void DeleteNodeOnlyLeftChild(BaseNode<BSTNode> deleteNode)
{
if (deleteNode.IsRoot)
{
_root = deleteNode.LeftNode;
}
else if (deleteNode.IsLeftNode)
{
deleteNode.ParentNode.InsertLeft(deleteNode.LeftNode);
}
else if (deleteNode.IsRightNode)
{
deleteNode.ParentNode.InsertRight(deleteNode.LeftNode);
}
}
/// <summary>
/// 删除只有右子树的节点
/// </summary>
/// <param name="deleteNode"></param>
private void DeleteNodeOnlyRightChild(BaseNode<BSTNode> deleteNode)
{
if (deleteNode.IsRoot)
{
_root = deleteNode.RightNode;
}
else if (deleteNode.IsLeftNode)
{
deleteNode.ParentNode.InsertLeft(deleteNode.RightNode);
}
else if (deleteNode.IsRightNode)
{
deleteNode.ParentNode.InsertRight(deleteNode.RightNode);
}
}
}
2、AVL
上述中的BST存在一个问题:即BST整个结构与节点的插入、删除的顺序有关系。当极端情况,整个搜索树可能像单向链表一样,搜索时间复杂度为O(n)。如下图所示

2.1 平衡因子
为了解决BST这一弊端,就引入了平衡二叉搜索树,即AVL。首先在BSTNode的基础上,增加了一个属性——平衡因子BalanceFactor。平衡因子即当前节点,左右子树的高度差。举例如下图所示:
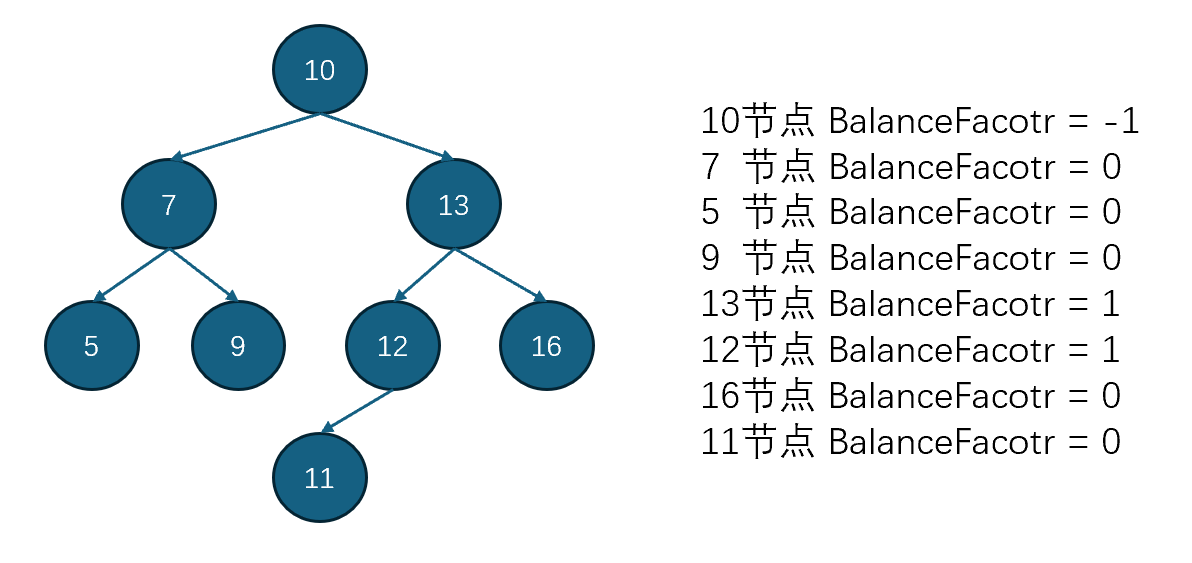
AVL即每一个节点的平衡因子绝对值小于等于1,即每个节点的左右子树高度差的绝对值小于1。
2.2 插入
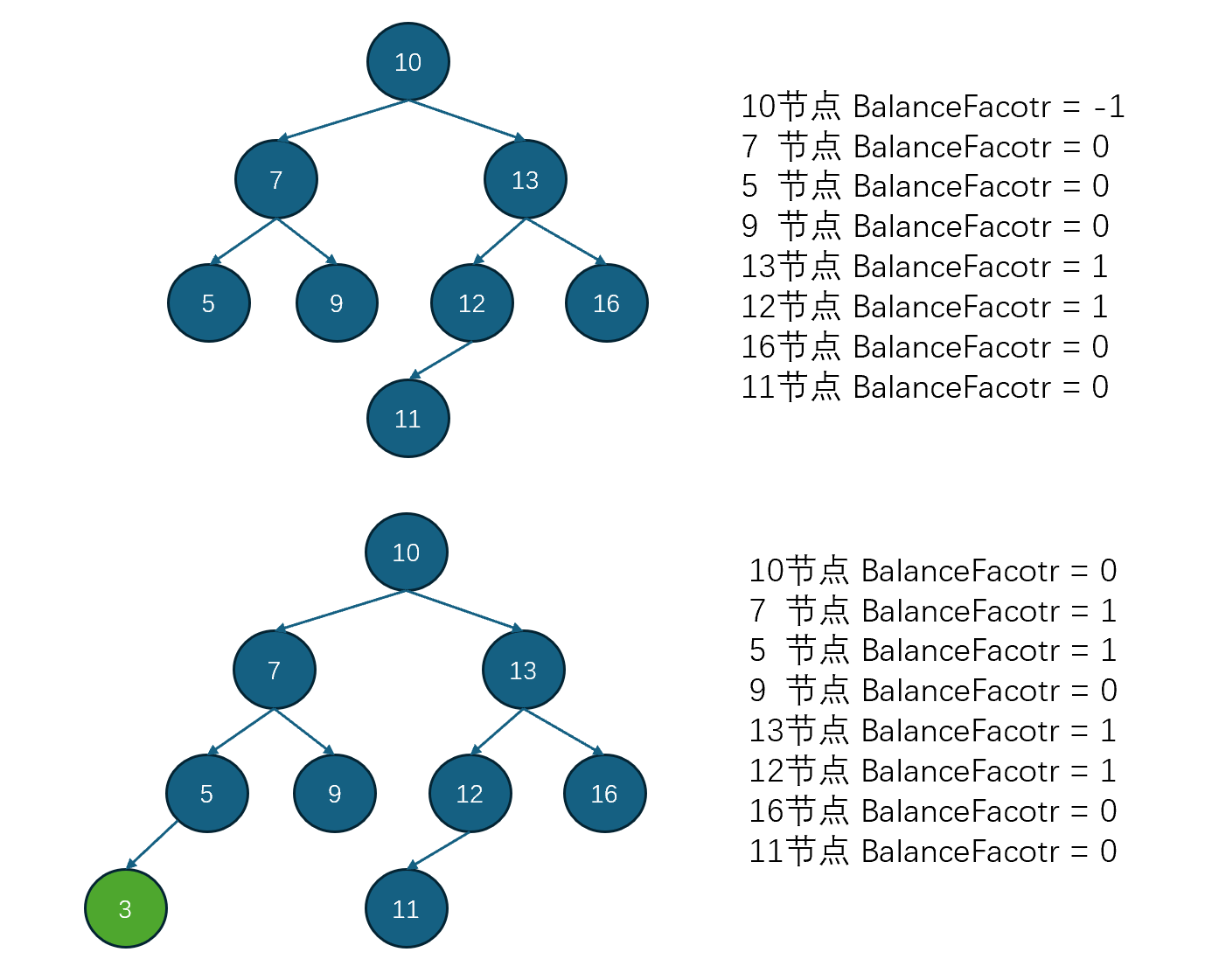
插入逻辑与BST大致相同,但是当插入结束后需要从当前节点往父节点方向更新平衡因子。如当前插入的左节点,则其父节点平衡因子+1,若为右节点,则其父节点的平衡因子-1,如下图所示。
当从插入节点往父节点方向更新平衡因子时,如果某个节点的平衡因子等于2或者-2,则需要做结构调整,可以一共分为左旋、右旋、左右旋、右左旋四个类型。
2.2.1 左旋
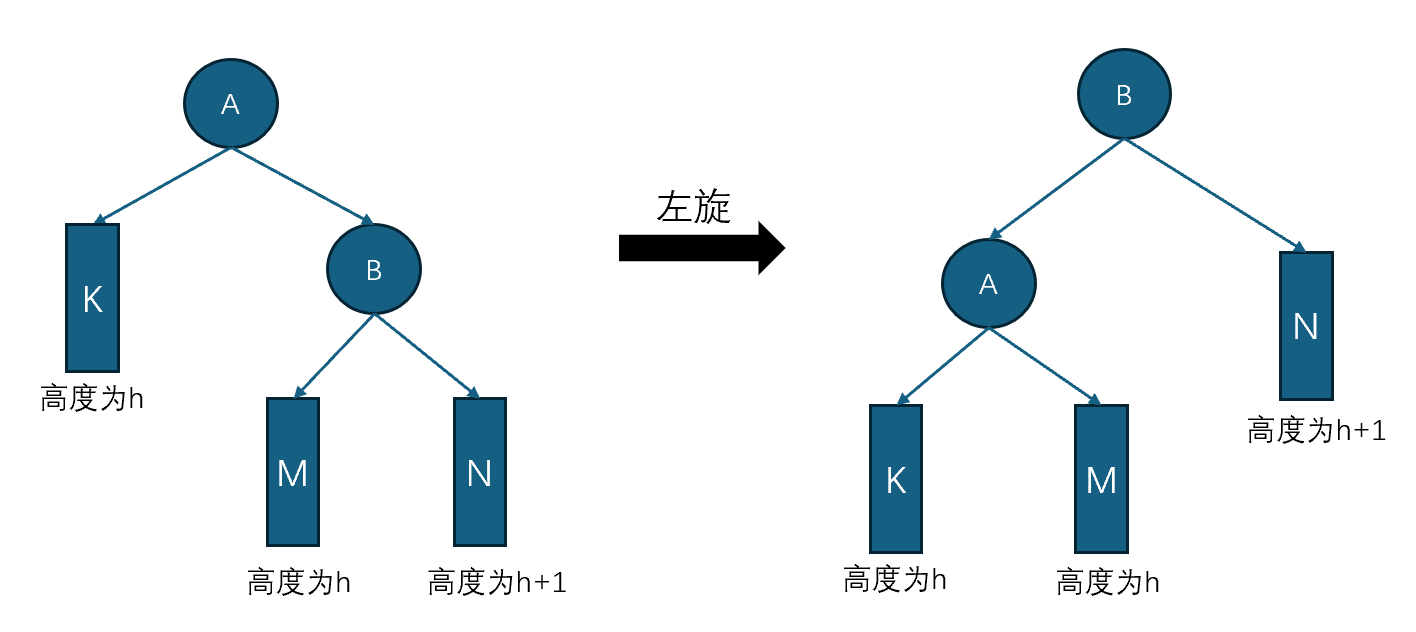
当某个节点不平衡的原因是因为右节点的右子树导致,则需要左旋。整个过程如下图所示:A节点平衡因子为-2,A节点不平衡的原因是由于其右节点B的右子树N引起的。整个左旋步骤为:将A的右节点B作为旋转后的新节点节点,A节点作为B节点的左节点,B的左节点作为A的右节点。
2.2.2 右旋
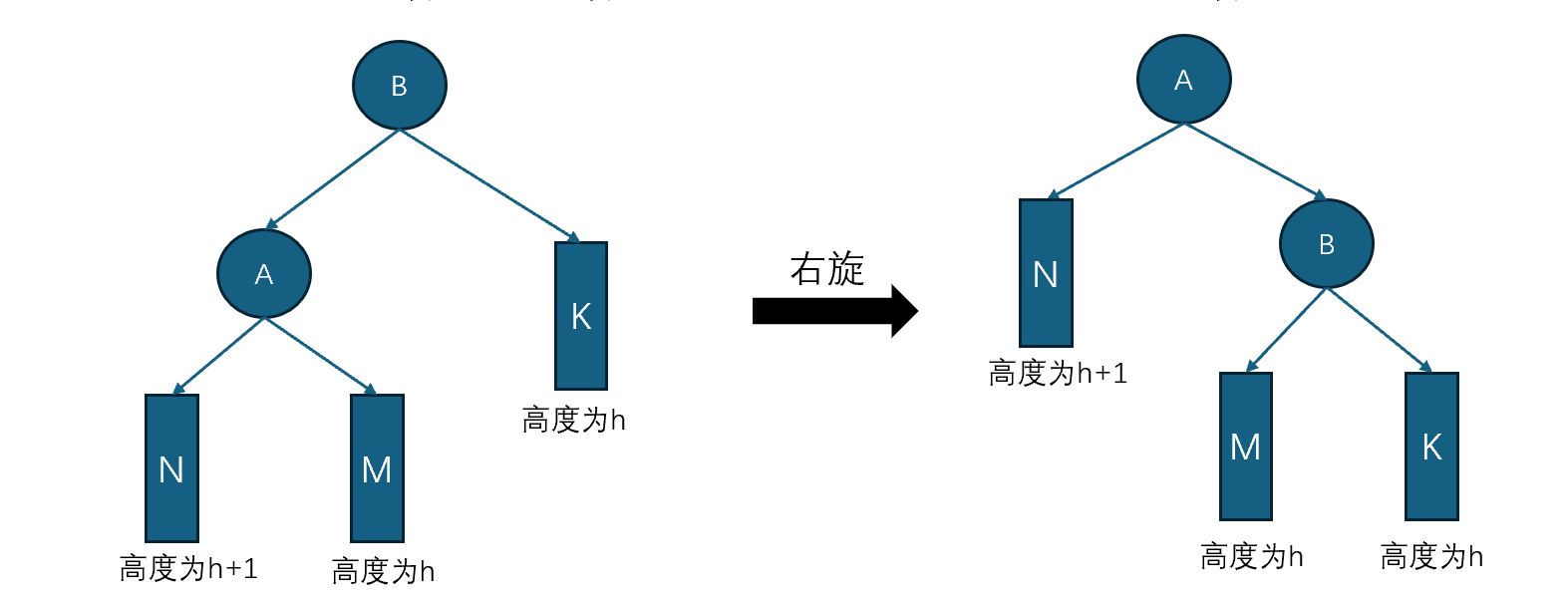
右旋过程与左旋过程对称,也可以理解为左旋的逆过程如下图所示:
2.2.3 左右旋
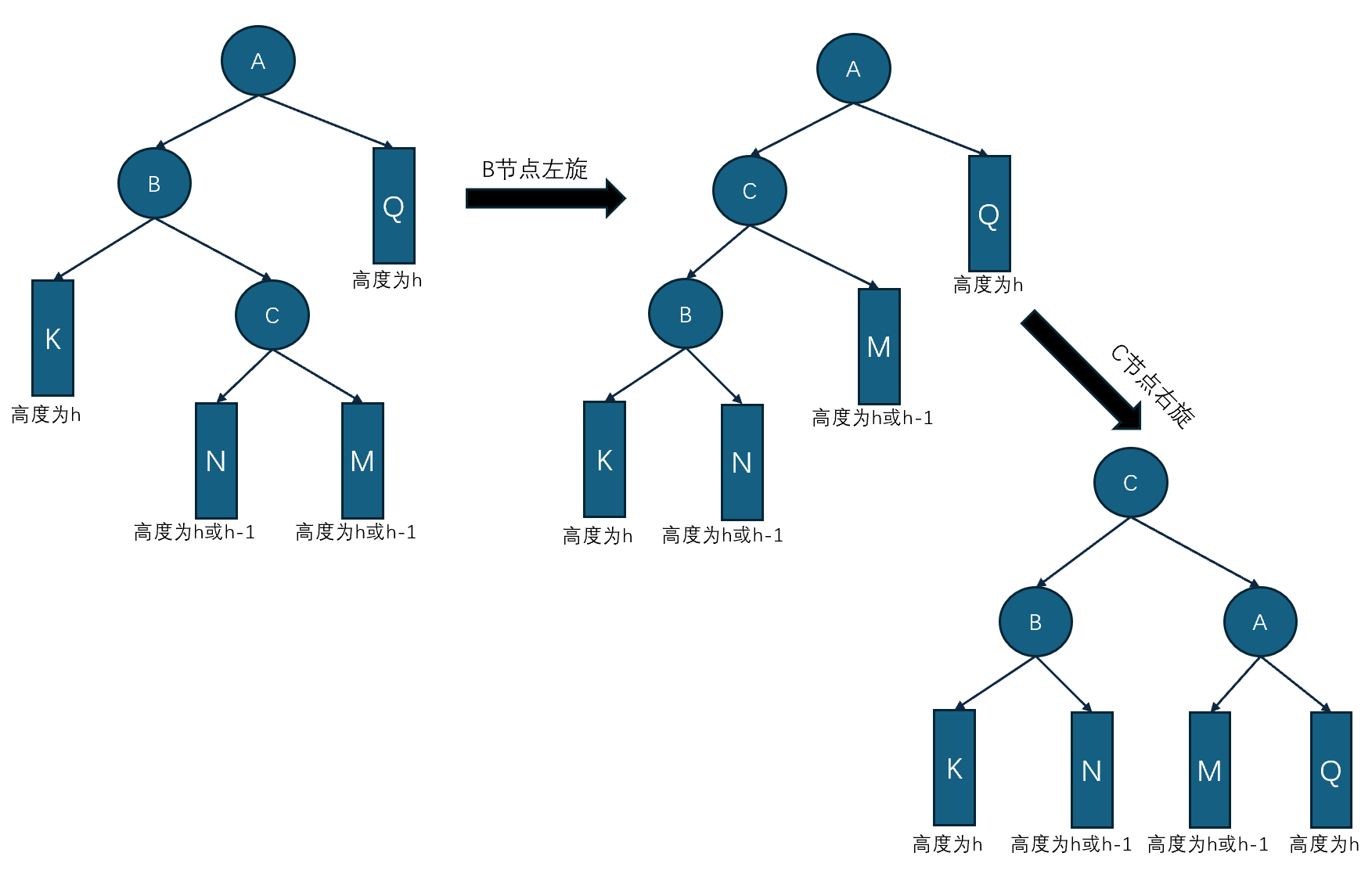
左右旋是因为不平衡的原因是左节点的右子树,即A节点不平衡的原因是其左节点B的右子树C+N+M。这种情况B节点先左旋,C节点再右旋
2.2.4 右左旋
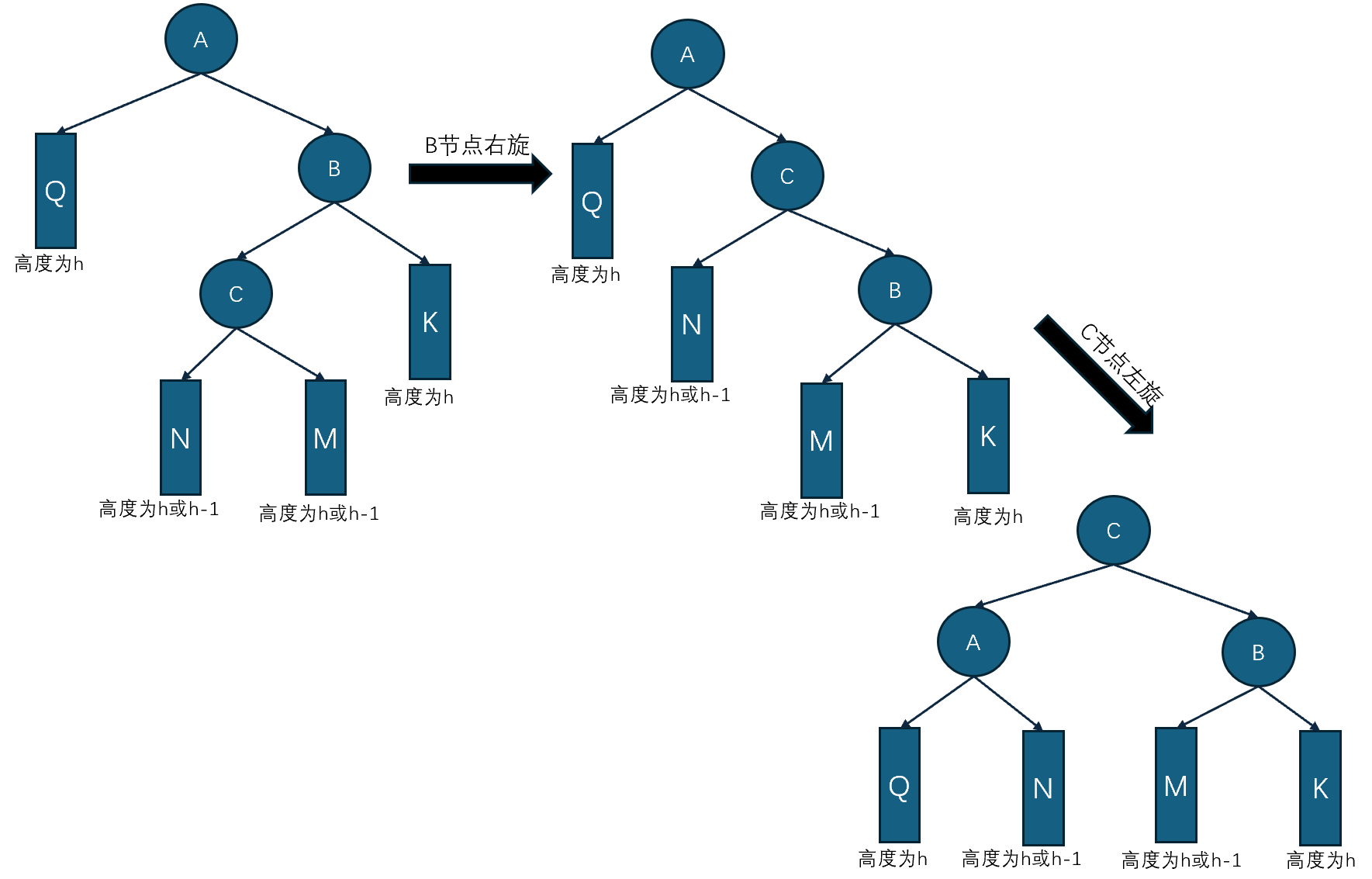
右左旋与左右旋对称,如下图所示:
2.2.5 终止更新条件
若当前插入的左节点,则其父节点平衡因子+1,若为右节点,则其父节点的平衡因子-1。当平衡因子为-2或2时,会根据失去平衡原因决定左旋、右旋、左右旋、右左旋。当前节点往父节点更新会有如下几种情况:
| 父节点平衡因子 | 父节点平衡因子(更新后) | 是否旋转 | 高度是否变化 | 旋转后的平衡因子 | |
| 插入左节点 | -1 | 0 | 否 | 否 | / |
| 0 | 1 | 否 | 是 | / | |
| 1 | 2 | 是 | 否 | 0 | |
| 插入右节点 | -1 | -2 | 是 | 否 | 0 |
| 0 | -1 | 否 | 是 | / | |
| 1 | 0 | 否 | 否 | / |
尤其要理解一点:仅仅是因为插入操作导致的某个节点旋转,旋转后该节点平衡因子一定为0,且整个子树高度与插入前相同,这个可以自己画几个例子想一想,很简单。
所以,显而易见,当插入节点往父节点方向更新平衡因子时,若更新后父节点的平衡因子为0时候,停止往上更新。
2.3 更新平衡因子变化证明过程
刚才提到不平衡的节点旋转后,平衡因子为0,但为了考虑左右旋方法的通用性,我们要证明一下平衡因子的变化过程,以左旋为例:

A节点平衡因子证明过程如下:
A.BalanceFactor(After) = h(K) - h(M) (左旋后)
A.BalanceFactor(Before) = h(K) - h(B) (左旋前)
h(B) = 1 + max(h(M), h(N)) (左旋前)
等式3代入等式2:
A.BalanceFactor(Before) = h(K) - 1 - max(h(M), h(N))
等式1 减等式4:
A.BalanceFactor(After) - A.BalanceFactor(Before) = h(K) - h(M) - h(K) + 1 + max(h(M), h(N))
A.BalanceFactor(After) - A.BalanceFactor(Before) = 1 + max(h(M)-h(M), h(N)-h(M))
A.BalanceFactor(After) - A.BalanceFactor(Before) = 1 + max(0, h(N)-h(M))
A.BalanceFactor(After) - A.BalanceFactor(Before) = 1 + max(0, - A.BalanceFactor(After) )
A.BalanceFactor(After) - A.BalanceFactor(Before) = 1 - min(0, A.BalanceFactor(After) )
A.BalanceFactor(After) = 1 + A.BalanceFactor(Before) - min(0, A.BalanceFactor(After) )
B节点平衡因子证明过程:
B.BalanceFactor(After) = h(A) - h(N) (左旋后)
B.BalanceFactor(Before) = h(M) - h(N) (左旋前)
h(A) = 1 + max( h(K), h(M))(左旋后)
等式3代入等式1
B.BalanceFactor(After) = 1 + max( h(K), h(M)) - h(N)
等式4-等式2:
B.BalanceFactor(After) - B.BalanceFactor(Before) = 1 + max( h(K), h(M)) - h(M)
B.BalanceFactor(After) - B.BalanceFactor(Before) = 1 + max( h(K)- h(M), 0)
B.BalanceFactor(After) - B.BalanceFactor(Before) = 1 + max( A.BalanceFactor(After), 0)
B.BalanceFactor(After) = B.BalanceFactor(Before) + 1 + max(A.BalanceFactor(After), 0)
2.4 删除
删除与BST的删除类似,但还是需要往父节点方向更新平衡因子。但与插入的时候更新平衡因子稍有不同。当删除节点为左节点时,父节平衡因子-1;当删除节点为右节点时,父节点平衡因子+1。且终止更新条件也与插入的更新条件恰好相反。这里我不做太多证明,详情见代码。
2.5 代码
public class AVLNode : BaseNode<AVLNode>
{
/// <summary>
/// 平衡因子
/// </summary>
private int _balanceFactor = 0;
public int BalanceFactor { get => _balanceFactor; }
public AVLNode(int value) : base(value) { }
/// <summary>
/// 修改平衡因子
/// </summary>
/// <param name="balanceFactor"></param>
public void ModifyBalanceFactor(int BalanceFactor)
{
_balanceFactor = BalanceFactor;
}
public void ModifyBalanceFactor(bool IsIncrease)
{
_balanceFactor += IsIncrease ? 1 : -1;
}
}
public class AVLTree : BaseTree<AVLNode>, IOperation
{
public AVLTree(int value)
{
_root = new AVLNode(value);
}
/// <summary>
/// 查询
/// </summary>
/// <param name="value"></param>
/// <returns></returns>
public Result Query(int value)
{
Result result = new Result();
if (Query(_root, value) == null)
{
result.Status = false;
result.Message = "No Such Node!";
}
else
{
result.Status = true;
}
return result;
}
/// <summary>
/// 删除
/// </summary>
/// <param name="value"></param>
/// <returns></returns>
public Result Delete(int value)
{
Result result = new Result() { Status = true };
AVLNode node = Query(_root, value);
if (node == null)
{
result.Status = false;
result.Message = "No Such Node";
}
else
{
Delete(node);
}
return result;
}
/// <summary>
/// 插入
/// </summary>
/// <param name="value"></param>
public void Insert(int value)
{
if (_root == null)
{
_root = new AVLNode(value);
}
else
{
Insert(_root, value);
}
}
private void RotateLeft(AVLNode rotateNode)
{
AVLNode newNode = rotateNode.RightNode;
if (!rotateNode.IsRoot)
{
if (rotateNode.IsLeftNode)
{
rotateNode.ParentNode.InsertLeft(newNode);
}
else
{
rotateNode.ParentNode.InsertRight(newNode);
}
}
else
{
_root = newNode;
}
rotateNode.InsertRight(newNode.LeftNode);
newNode.InsertLeft(rotateNode);
rotateNode.ModifyBalanceFactor(rotateNode.BalanceFactor - Math.Min(0, newNode.BalanceFactor) + 1);
newNode.ModifyBalanceFactor(newNode.BalanceFactor + Math.Max(0, rotateNode.BalanceFactor) + 1); ;
}
/// <summary>
/// 右旋
/// </summary>
/// <param name="rotateNode"></param>
private void RotateRight(AVLNode rotateNode)
{
AVLNode newNode = rotateNode.LeftNode;
if (!rotateNode.IsRoot)
{
if (rotateNode.IsLeftNode)
{
rotateNode.ParentNode.InsertLeft(newNode);
}
else
{
rotateNode.ParentNode.InsertRight(newNode);
}
}
else
{
_root = newNode;
}
rotateNode.InsertLeft(newNode.RightNode);
newNode.InsertRight(rotateNode);
rotateNode.ModifyBalanceFactor(rotateNode.BalanceFactor - Math.Max(0,newNode.BalanceFactor) - 1);
newNode.ModifyBalanceFactor(newNode.BalanceFactor + Math.Min(0, rotateNode.BalanceFactor) - 1); ;
}
/// <summary>
/// 往上更新平衡因子
/// </summary>
/// <param name="node"></param>
private void UpdateBalanceFactor(AVLNode node)
{
if(node.BalanceFactor < -1 || node.BalanceFactor > 1)
{
KeepBalance(node);
return;
}
if (node.ParentNode != null)
{
if (node.IsLeftNode)
{
node.ParentNode.ModifyBalanceFactor(true);
}
else if (node.IsRightNode)
{
node.ParentNode.ModifyBalanceFactor(false);
}
if(node.ParentNode.BalanceFactor != 0)
{
UpdateBalanceFactor(node.ParentNode);
}
}
}
/// <summary>
/// 删除节点时往上更新平衡因子
/// </summary>
/// <param name="node"></param>
private void UpdateBalanceFactorWhenDelete(AVLNode node)
{
if(node.BalanceFactor == -1 || node.BalanceFactor == 1)
{
return;
}
if (node.BalanceFactor < -1 || node.BalanceFactor > 1)
{
KeepBalance(node);
UpdateBalanceFactorWhenDelete(node.ParentNode);
return;
}
if(node.ParentNode != null)
{
if (node.IsLeftNode)
{
node.ParentNode.ModifyBalanceFactor(false);
}
else if (node.IsRightNode)
{
node.ParentNode.ModifyBalanceFactor(true);
}
if(node.ParentNode.BalanceFactor != 1 && node.ParentNode.BalanceFactor != -1)
{
UpdateBalanceFactorWhenDelete(node.ParentNode);
}
}
}
/// <summary>
/// 旋转平衡
/// </summary>
/// <param name="node"></param>
private void KeepBalance(AVLNode node)
{
if(node.BalanceFactor < 0)
{
if(node.RightNode.BalanceFactor > 0)
{
RotateRight(node.RightNode);
}
RotateLeft(node);
}
else
{
if(node.LeftNode.BalanceFactor < 0)
{
RotateLeft(node.LeftNode);
}
RotateRight(node);
}
}
private void Insert(AVLNode node, int value)
{
if(value <= node.Value)
{
if(node.LeftNode == null)
{
node.InsertLeft(new AVLNode(value));
UpdateBalanceFactor(node.LeftNode);
}
else
{
Insert(node.LeftNode, value);
}
}
else
{
if (node.RightNode == null)
{
node.InsertRight(new AVLNode(value));
UpdateBalanceFactor(node.RightNode);
}
else
{
Insert(node.RightNode, value);
}
}
}
private AVLNode Query(AVLNode node, int value)
{
if (node.Value == value)
{
return node;
}
if (value > node.Value)
{
if (node.HaveRightNode)
{
return Query(node.RightNode, value);
}
else
{
return null;
}
}
else
{
if (node.HaveLeftNode)
{
return Query(node.LeftNode, value);
}
else
{
return null;
}
}
}
private void Delete(AVLNode node)
{
if (node.IsLeaf)
{
if (node.IsLeftNode)
{
node.ParentNode.InsertLeft(null);
node.ParentNode.ModifyBalanceFactor(false);
UpdateBalanceFactorWhenDelete(node.ParentNode);
}
else
{
node.ParentNode.InsertRight(null);
node.ParentNode.ModifyBalanceFactor(true);
UpdateBalanceFactorWhenDelete(node.ParentNode);
}
}
else if (node.HasBothNode)
{
AVLNode exchangeNode = node.RightNode;
while (exchangeNode.LeftNode != null)
{
exchangeNode = exchangeNode.LeftNode;
}
node.ChangeValue(exchangeNode.Value);
Delete(exchangeNode);
}
else
{
if (node.HaveLeftNode)
{
if (node.IsLeftNode)
{
node.ParentNode.InsertLeft(node.LeftNode);
node.ParentNode.ModifyBalanceFactor(false);
UpdateBalanceFactorWhenDelete(node.ParentNode);
}
else if (node.IsRightNode)
{
node.ParentNode.InsertRight(node.LeftNode);
node.ParentNode.ModifyBalanceFactor(true);
UpdateBalanceFactorWhenDelete(node.ParentNode);
}
else
{
_root = node.LeftNode;
}
}
else
{
if (node.IsLeftNode)
{
node.ParentNode.InsertLeft(node.RightNode);
node.ParentNode.ModifyBalanceFactor(false);
UpdateBalanceFactorWhenDelete(node.ParentNode);
}
else if (node.IsRightNode)
{
node.ParentNode.InsertRight(node.RightNode);
node.ParentNode.ModifyBalanceFactor(true);
UpdateBalanceFactorWhenDelete(node.ParentNode);
}
else
{
_root = node.RightNode;
}
}
}
}
}
没有做可视化演示,可以用中序遍历测试一下
/// <summary>
/// 中序遍历
/// </summary>
/// <typeparam name="T"></typeparam>
/// <param name="node"></param>
/// <returns></returns>
private static List<int> OrderBy<T>(BaseNode<T> node) where T:BaseNode<T>
{
List<int> result = new List<int>();
if(node != null)
{
result.AddRange(OrderBy(node.LeftNode));
result.Add(node.Value);
result.AddRange(OrderBy(node.RightNode));
}
return result;
}
/// <summary>
/// 中序遍历并返回平衡因子
/// </summary>
/// <param name="node"></param>
/// <returns></returns>
private static List<Tuple<int, int>> OrderByWithBalance(AVLNode node)
{
List<Tuple<int, int>> result = new List<Tuple<int, int>>();
if (node != null)
{
result.AddRange(OrderByWithBalance(node.LeftNode));
result.Add(new Tuple<int, int>(node.Value, node.BalanceFactor));
result.AddRange(OrderByWithBalance(node.RightNode));
}
return result;
}
写到这里实在不想写了。。。
我的项目结构如下,想要整个项目的可以私信我发你:




















 109
109

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








