【漫话机器学习系列】205.度（夹角）（Span）

什么是矩阵的“度（夹角）”与“张成空间”——从向量到空间的几何直观

在学习线性代数的过程中，我们经常会遇到“张成空间（Span）”这个概念。对于初学者而言，这个词听起来抽象又遥远，甚至容易混淆于“维度”、“线性无关”这些概念中。

今天我们就借助一张生动直观的手绘图，来全面理解“张成空间”的几何意义，并从图中扩展出一个更常见的问题：向量之间的夹角（或称“度”）在空间中的角色。

---

一、什么是张成（Span）？

我们先来看图中这段话：

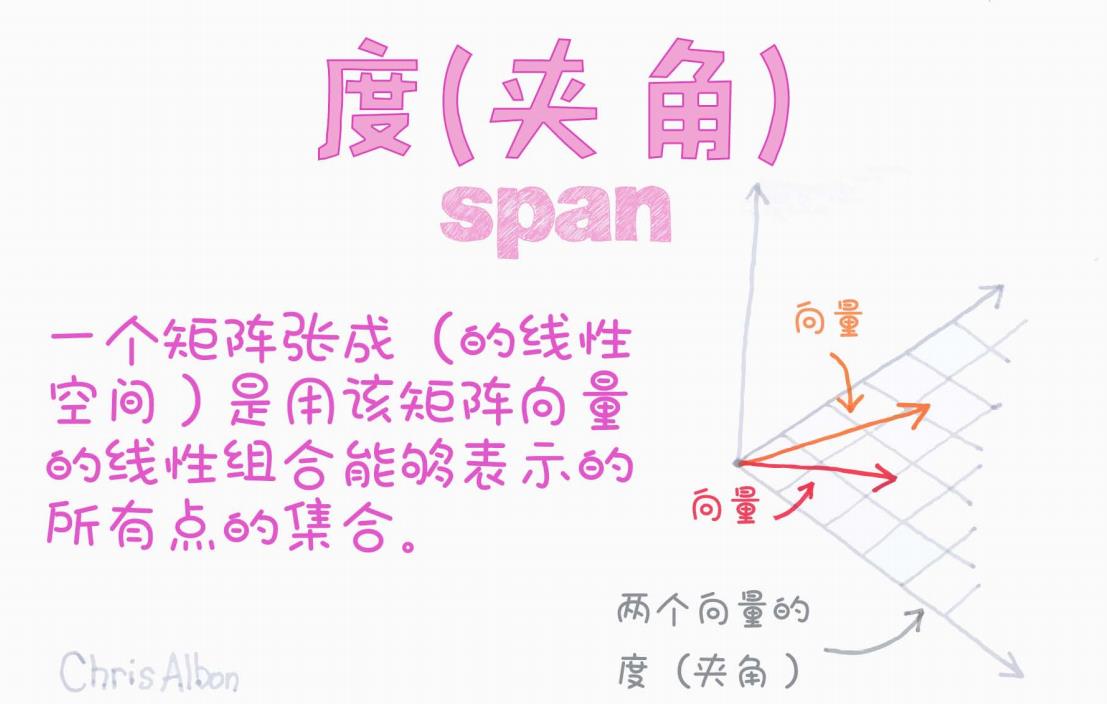
一个矩阵张成（的线性空间）是用该矩阵向量的线性组合能够表示的所有点的集合。

这其实是“张成空间”的一个非常准确的定义。我们可以逐句拆解一下：

• 矩阵向量：假设我们有两个向量，分别为 v₁ 和 v₂，它们可能来自一个矩阵的列向量。

• 线性组合：我们可以用任意实数 a、b 来构造：a*v₁ + b*v₂

• 所有点的集合：这个组合中，a、b 可任意取值（实数），就可以构造出无数个新的向量，也就构成了一个“空间”。

通俗理解：

如果你把向量想象成“方向”，那么“张成空间”就像是在这些方向上尽可能延伸拉开的“整个区域”。
在二维中，这通常是一个平面；在三维中，可能是一个线、一个平面，或整个空间，取决于向量的数量与线性相关性。

---

二、图片中的几何解读

图片右侧用几何方式表达了这个概念：

• 两个原点出发的箭头代表两个向量

• 从这两个向量出发，用不同权重组合生成了一张平面网格

• 这个“网格”就是这两个向量张成的平面

这个图特别好的地方在于，它强调了：

张成空间是从“方向 + 尺度”的无限组合构造出来的一个空间。

你不需要去死记公式，只要理解：你可以沿着这些向量“加权走”，就能到达张成空间的任意一个点。

---

三、那“度（夹角）”又是啥意思？

图片左上角写着大字：“度（夹角） span”。右下角补充：

两个向量的度（夹角）

这提示我们另一个重要概念：向量之间的夹角。

向量夹角的数学定义：

对于两个向量 a 和 b，它们的夹角 θ 满足：

这里：

• a⋅b：是向量点积

• ∥a∥,∥b∥：分别是向量的模长

夹角反映了两个向量之间的“相似程度”：

• θ = 0°：完全同方向

• θ = 90°：正交，彼此无关

• θ = 180°：完全反方向

和张成空间的关系？

夹角的大小直接影响张成空间的“形状”和“维度”：

• 如果两个向量夹角为 0 或 180°（共线），它们张成的空间就是“一条线”

• 如果夹角不为 0/180°，它们张成的是一个“二维平面”

• 如果你有三个彼此不共面的向量（在三维空间中），就能张成整个三维空间

所以，“夹角”是判断向量之间是否能扩展成更高维空间的关键！

---

四、应用与延伸

理解张成空间和夹角，不只是理论上的概念，它在许多实际应用中都有重要作用：

应用领域	使用场景
机器学习	判断特征向量是否冗余（是否线性相关）
信号处理	判断信号是否可以由基信号表示（傅里叶变换等）
图像压缩	选择能张成原始图像空间的大致子空间，保留重要信息
物理建模	利用基向量张成运动空间，表示多维运动
NLP 词向量表示	多个词向量张成的空间，用于推测词汇之间的关系

---

五、总结

通过这张图，我们可以深刻理解两个核心概念：

张成空间（Span）：

是由向量的线性组合构成的所有点的集合，本质上描述了“这些向量能够覆盖的空间”。

向量之间的夹角：

是判断这些向量是否能扩展出“有体积”的空间的关键。

---

一句话总结： 张成空间告诉我们“我们能去哪儿”，而夹角告诉我们“我们之间差多远”。

这两个概念结合在一起，是我们理解线性代数、建模、特征工程等核心问题的基础。