【字符串算法】扩展 KMP 算法（Z-Algorithm）

【字符串算法】扩展 KMP 算法（Z-Algorithm）

---

算法专栏：扩展 KMP 算法
算法竞赛：字符串，模式匹配，扩展 KMP 算法
洛谷专栏：模板，字符串，扩展 KMP 算法
洛谷模板：P5410 扩展 KMP（Z 函数）
题目链接：洛谷 P5410 扩展 KMP

题目描述：
给定两个字符串 $a,b$，你要求出两个数组：

• $b$ 的 $z$ 函数数组 $z$，即 $b$ 与 $b$ 的每一个后缀的 LCP 长度。
• $b$ 与 $a$ 的每一个后缀的 LCP 长度数组 $p$。

对于一个长度为 $n$ 的数组 $a$，设其权值为 ${\mathrm{xor}}_{i=1}^{n}i\times (a_i+1)$。

输入格式：
两行两个字符串 $a,b$。
输出格式：
第一行一个整数，表示 $z$ 的权值。第二行一个整数，表示 $p$ 的权值。

数据范围：
对于第一个测试点，$|a|,|b|\le 2\times 10^3$。
对于第二个测试点，$|a|,|b|\le 2\times 10^5$。
对于 $100\%$ 的数据，$1\le |a|,|b|\le 2\times 10^7$，所有字符均为小写字母。

---

扩展 KMP（Z-Algorithm）

扩展 KMP（exKMP）算法，也被称作 Z 函数（Z-Algorithm），顾名思义就是 KMP 算法的扩展算法，是一种字符串模式匹配算法，可以在 $\mathcal{O}(n)$ 的时间复杂度内求解字符串后缀与前缀的最长公共前缀（LCP）长度问题。

---

问题描述

给定两个字符串 $a,b$，你要求出两个数组：

• $b$ 的 $z$ 函数数组 $z$，即 $b$ 与 $b$ 的每一个后缀的 LCP 长度。
• $b$ 与 $a$ 的每一个后缀的 LCP 长度数组 $p$。

LCP 长度（Longest Common Prefix），指两个字符串或序列的最长公共前缀长度。在此问题中，两个字符串分别为给定串和给定串的其中某个后缀子串。

对于一个长度为 $n$ 的字符串 $S[0\sim n-1]$（字符串 $b$），$z$ 数组定义为：

• $z[0]=n$（整个字符串与自身完全匹配）；
• 对于 $i>0$，$z[i]$ 表示从位置 $i$ 开始的子串 $S[i\sim n-1]$ 与 $S$ 的前缀 $S[0\sim n-1]$ 的最长公共前缀的长度。

对于一个长度为 $m$ 的字符串 $S^{\prime }[0\sim m-1]$（字符串 $a$），$p$ 数组定义为：

• 对于 $i\ge 0$，$p[i]$ 表示从位置 $i$ 开始的子串 $S^{\prime }[i\sim m-1]$ 与 $S$ 的前缀 $S[0\sim n-1]$ 的最长公共前缀的长度。

对数组 $p$ 和数组 $z$ 的定义进行观察可以发现，可以通过将字符串 $a$ 拼接到字符串 $b$ 后求 $z$ 数组，间接求解 $p$ 数组。

---

实例展示

字符串 $b$：

事物	内容	内容	内容	内容	内容	内容	内容
字符串 $b$	$a$	$a$	$a$	$b$	$b$	$a$	$a$
数组 $z$	$7$	$2$	$1$	$0$	$0$	$2$	$1$

字符串 $a$：

事物	内容	内容	内容	内容	内容	内容	内容	内容	内容	内容
字符串 $a$	$a$	$a$	$a$	$a$	$a$	$b$	$b$	$b$	$a$	$a$
数组 $p$	$3$	$3$	$5$	$2$	$1$	$0$	$0$	$0$	$2$	$1$

---

扩展 KMP 算法

算法思想

扩展 KMP 算法是根据前面求解出来的结果递推式地向后扩展求解。

扩展 KMP 算法在处理字符串时是从前向后依次遍历地处理每一位字符，对于一个字符串 $S[0\sim n-1]$，如果已经知道 $z[0\sim i-1]$ 的结果，就能递推式地求解出 $z[i]$ 的值。

---

算法思路

对于一个长度为 $n$ 的字符串 $S[0\sim n-1]$，求解其 $z$ 数组，已知 $z[0\sim i-1]$ 时，对于 $0\le l<i$，维护一个 $l$，使 $l+z[l]-1$ 最大，记作 $r$，即 $r=l+z[l]-1$。

将字符串 $S$ 表示在图片上，如图所示：

根据 $z$ 数组的定义，可以知道 $s[0\sim r-l]=s[l\sim r]$，即图中蓝色的两部分是完全相同的，分两种情况进行讨论：

（情况一）：

当 $i-l+z[i-l]-1\le r-l$（即 $i+z[i-l]-1\le r$）时，由蓝色部分一致性可知 $z[i]=z[i-l]$。

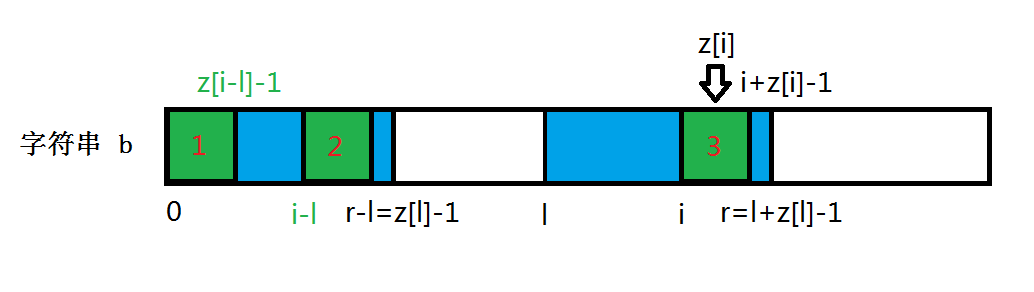
如图所示：

• $Part(1)$ 部分即 $S[0\sim z[i-l]-1]$；
• $Part(2)$ 部分即 $S[i-l\sim i-l+z[i-l]-1]$；
• $Part(3)$ 部分即 $S[i\sim i+z[i-l]-1]$，即待求部分。
• $Part(4)$ 部分即 $S[i-l\sim z[l]-1]$，即从 $i-l$ 到第一个蓝色部分最后。
• $Part(5)$ 部分即 $S[i\sim l+z[l]-1]$，即从 $i$ 到第二个蓝色部分最后。

思路过程：

1. 已知 $Part(5)$ 部分，即 $S[i\sim l+z[l]-1]$，找到与 $Part(5)$ 对应的 $Part(4)$ 部分，即 $S[i-l\sim z[l]-1]$；
2. 标记出从 $i-l$ 开始的后缀的前缀中与前缀的最长公共部分，记作 $Part(2)$ 部分，即 $S[i-l\sim i-l+z[i-l]-1]$，对应的前缀部分标记为 $Part(1)$ 部分，即 $S[0\sim z[i-l]-1]$；
3. 从 $Part(5)$ 部分找出与 $Part(2)$ 对应的部分，即 $S[i\sim i+z[i-l]-1]$，标记为 $Part(3)$ 部分；
4. 由蓝色部分一致性可知 $Part(2,3)$ 两部分完全相同，且 $Part(1,2)$ 两部分完全相同，则 $Part(1,3)$ 两部分完全相同；
5. 由 $z$ 数组的定义可知，$Part(1)$ 部分和 $Part(2)$ 部分的下一位字符不相同，则 $Part(1)$ 部分和 $Part(3)$ 部分的下一位字符不相同，故可得 $z[i]=z[i-l]$。

（情况二）：

当 $i-l+z[i-l]-1>r-l$（即 $i+z[i-l]-1>r$）时，$z[i]=l+z[l]-i$（即 $z[i]=r-i+1$），超出蓝色部分处需枚举判断，并更新 $l=i,r=i+z[i]-1$。

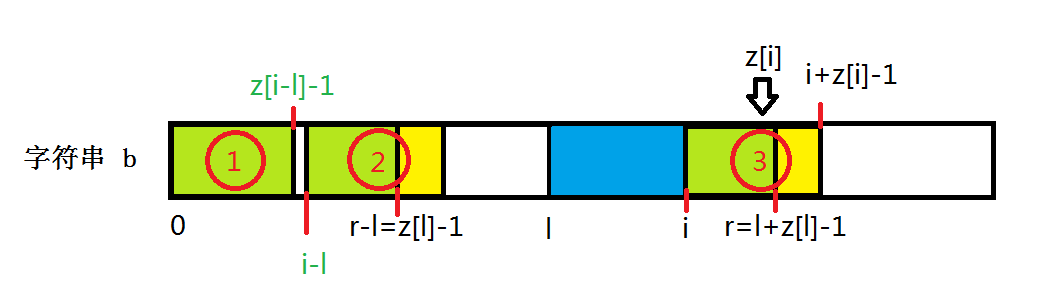
根据情况一所述，可知 $Part(2,3)$ 两部分的 $S[i-l\sim r-l]=S[i\sim r]$，而超出 $r-l,r$ 的图中黄色部分就需要枚举来判断是否相同了，若黄色部分中枚举到的位上的字符相同，这时维护的 $l,r$ 就需要更新，$l=i,r=i+z[i]-1$。

根据上述两种情况综合来看，$z[i]=\min (z[i-l],l+z[l]-i)$ 或者 $z[i]=\min (z[i-l],r-i+1)$，再根据情况枚举即可。

算法思路就是如此了，接下来看一看算法的公式证明。

---

公式证明

参考博客：扩展 KMP。

同样，对于字符串 $S$，我们从下标 $0$ 开始计数。

---

结论

对于 $i>0$，对任意的 $0\le l<i$ 都有：

$$\forall 0\le x<\min (z[i-l],l+z[l]-i),S[(i)+(x)]=S[(0)+(x)]$$

---

证明

$$\begin{array}{rl}& S[(i)+(x)]\\ & =S[(l)+(i+x-l)]\\ & =S[(0)+(i+x-l)](i+x-l<z[l]⟹x<l+z[l]-i)\\ & =S[(i-l)+(x)]\\ & =S[(0)+(x)](x<z[i-l])\end{array}$$

---

说明

这个结论说明对于 $z[i]$ 至少是 $\min (z[i-l],l+z[l]-i),\forall 0\le l<i$，这属于是一个递推式的初始化结果，根据上述证明过程不能确保 $x\ge \min (z[i-l],l+z[l]-i),\forall 0\le l<i$ 时，$S[(0)+(x)]\ne S[(i)+(x)]$，所以还要枚举后续位上的字符更新 $z[i]$。

在算法过程中，如果我们维护 $r={\max }_{l=0}^{i-1}(l+z[l])$，并且只需在枚举后续位上的字符更新 $z[i]$ 时更新 $r$，则 $r$ 被更新最多会有 $N$ 次，可以达到 $\mathcal{O}(N)$ 的时间复杂度。

---

AC Code

注意：在最后求异或和时要开 long long 类型，会爆 int。

参考代码（一）

#include <bits/stdc++.h>
using namespace std;
const int N = 2e7+10;
char s[N<<1],a[N],b[N];
int z[N<<1],len,len_a,len_b;
void z_algorithm()
{
	int l=0;
	for (int i=1;i<len;i++)
	{
		if (l+z[l]>i) z[i]=min(z[i-l],l+z[l]-i);
		while (i+z[i]<len&&s[z[i]]==s[z[i]+i]) z[i]++;
		if (i+z[i]>l+z[l]) l=i;
	}
	z[0]=len_b;
}
int main()
{
	scanf("%s%s",a,b);
	len_a=strlen(a),len_b=strlen(b);
	strcpy(s,b);
	s[len_b]='#';
	strcpy(s+len_b+1,a);
	len=strlen(s);
	//puts(s);
	z_algorithm();
	long ans=0;
	for (int i=0;i<len_b;i++) ans^=1LL*(i+1)*(z[i]+1);
	printf("%lld\n",ans);
	ans=0;
	for (int i=len_b+1;i<len;i++) ans^=1LL*(i-len_b)*(z[i]+1);
	printf("%lld\n",ans);
	return 0;
}

参考代码（二）

#include <bits/stdc++.h>
using namespace std;
const int N = 2e7+10;
char a[N],b[N];
int nxt[N],ext[N];
void z_next()
{
	int len=strlen(b+1);
	nxt[1]=len;
	int l=1,r=1;
	for (int i=2;i<=len;i++)
	{
		if (i<=r) nxt[i]=min(nxt[i-l+1],r-i+1);
		while (i+nxt[i]<=len&&b[1+nxt[i]]==b[i+nxt[i]]) nxt[i]++;
		if (i+nxt[i]-1>r) l=i,r=i+nxt[i]-1;
	}
}
void z_extend()
{
	int len_a=strlen(a+1),len_b=strlen(b+1);
	int l=0,r=0;
	for (int i=1;i<=len_a;i++)
	{
		if (i<=r) ext[i]=min(nxt[i-l+1],r-i+1);
		while (i+ext[i]<=len_a&&ext[i]+1<=len_b&&a[i+ext[i]]==b[1+ext[i]]) ext[i]++;
		if (i+ext[i]-1>r) l=i,r=i+ext[i]-1;
	}
}
int main()
{
	scanf("%s%s",a+1,b+1);
	z_next(),z_extend();
	long long ans=0;
	for (int i=1;i<=strlen(b+1);i++) ans^=1LL*i*(nxt[i]+1);
	printf("%lld\n",ans);
	ans=0;
	for (int i=1;i<=strlen(a+1);i++) ans^=1LL*i*(ext[i]+1);
	printf("%lld\n",ans);
	return 0;
}

End

感谢观看，如有问题欢迎指出。

更新日志

1. 2025/08/21 开始书写本篇 优快云 博客。
2. 2025/08/23 本篇 优快云 博客第一次完稿并发布。
3. 2025/09/06 对本篇 优快云 博客进行了第一次更新，修改了一些单词拼写错误，优化了部分排版形式，优化了一些数学公式表达形式，更改了一些不严谨的表达，更改了文章封面图片。
4. 2025/09/10 对本篇 优快云 博客进行了第二次更新，在算法思路方面有较大调整，调整了算法思路的逻辑及排版，并且修改了部分语言表述和布局排版。

本篇博客同步于洛谷文章广场，洛谷用户：ZZA000HAH。