Day 55 序列预测任务介绍

原创于 2025-11-27 14:26:45 发布 · 604 阅读

8 ·

CC 4.0 BY-SA版权

文章标签：

#深度学习 #机器学习

Python打卡训练营专栏收录该内容

54 篇文章

订阅专栏

@浙大疏锦行

今日任务：

序列预测介绍：单步预测；多步预测（2种方式）
序列数据的处理：滑动窗口
多输入多输出任务的思路
经典机器学习在序列任务上的劣势

作业：手动构造类似的数据集（如cosx数据），观察不同的机器学习模型的差异

序列预测任务

序列预测：数据存在先后关系（顺序），任务是根据已有的历史数据预测未来的数据。比如，股票价格预测（根据过去30天预测第31天），文本单词预测等。

滑动窗口

在结构化数据中，处理监督学习问题时，存在的是“样本—标签”数据对。而在序列任务中，也有这样类似的数据对“x-y”，实现的方法是滑动窗口（类似卷积核的滑动）。

通过设置不同的时间步（seq_length）来完成下一个时间步的预测。比如在下面的例子中，就得到了 "[10,20,30] --> 40" 的数据对。

注：最后的[70,80,90]不能作为输入(无后续值作为目标)，故生成样本数：len(data) - seq_length

data = [10,20,30,40,50,60,70,80,90]
seq_length = 3
X = [
  [10, 20, 30],  # 用前3步预测第4步 -> 40
      [20, 30, 40],  # 用2-4步预测第5步 -> 50
          [30, 40, 50],  # 用3-5步预测第6步 -> 60
              [40, 50, 60],  # 用4-6步预测第7步 -> 70
                  [50, 60, 70],  # 用5-7步预测第8步 -> 80
                      [60, 70, 80]   # 用6-8步预测第9步 -> 90
]

y = [40, 50, 60, 70, 80, 90]  # 每个X对应的下一个值

预测方式

之前的结构化数据是独立同分布的，可以完成一步到位的映射；而序列数据由于自身的时间顺序性，只能一步一步地、递归地预测。

根据每一次预测的时刻数量，可分为单步预测和多步预测。

（1）单步预测：一次只预测下一时刻，多输入单输出。比如上面例子中的 [10,20,30] --> 40。

（2）多步预测：一次预测多个时刻，多输入多输出。

递归式（滚动预测）：先用预测第81天的，再用81天的预测数据和历史数据预测第82天的，以此类推，这种方式会造成误差的累积。
直接式：一次性输出未来多个时刻的值。如输入 x60-x80，输出 x81-x90，不累积误差

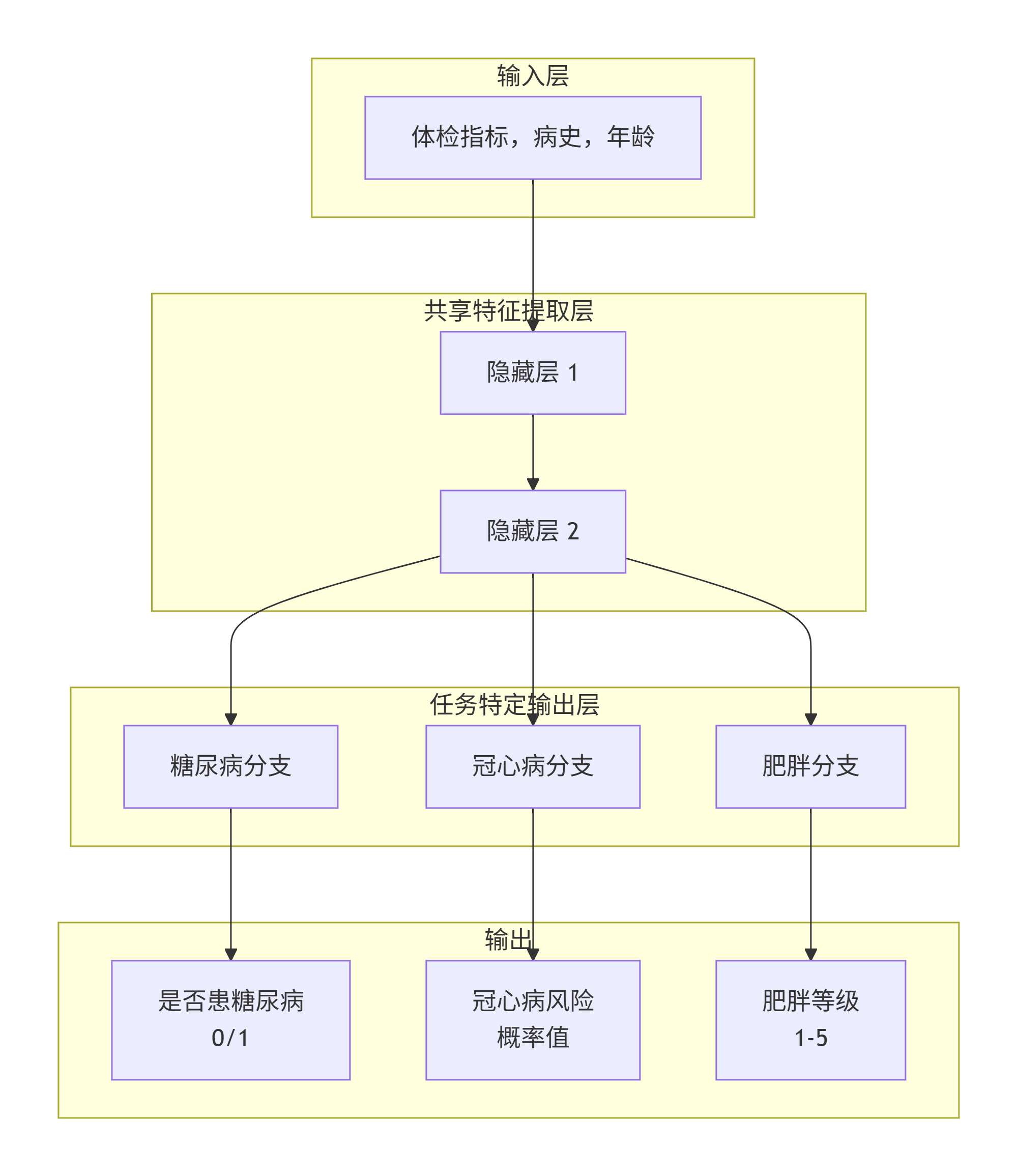
多输入多输出任务

输入：血压、血糖、胆固醇、病史、年龄

输出：

是否患糖尿病 (0/1) -> 任务A：二分类

冠心病风险 (概率值) -> 任务B：回归

肥胖等级 (1-5) -> 任务C：多分类

上面的例子是一个多输入多输出（MIMO）的问题，由于传统的机器学习模型默认单输出，针对这类MIMO问题可以由MLP实现，思路如下：

独立建模：直接拆分为多个多输入单输出的任务，可能丢失预测标签间的影响
联合建模：通过共享表示和任务特定分支，同时、协同地预测多个相关目标变量，最终损失函数是三个任务损失函数的加权和（权重分配）

实战

（1）准备工作：设置全局随机种子，复用之前的函数

# 准备工作

import numpy as np
import random
import os
import torch
import matplotlib.pyplot as plt
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_squared_error
import warnings
warnings.filterwarnings("ignore")


# 设置随机种子确保结果可复现，全局随机函数
def set_seed(seed=42, deterministic=True):
    """
    设置全局随机种子，确保实验可重复性
    
    参数:
        seed: 随机种子值，默认为42
        deterministic: 是否启用确定性模式，默认为True
    """
    # 设置Python的随机种子
    random.seed(seed) 
    os.environ['PYTHONHASHSEED'] = str(seed) # 确保Python哈希函数的随机性一致，比如字典、集合等无序
    
    # 设置NumPy的随机种子
    np.random.seed(seed)
    
    # 设置PyTorch的随机种子
    torch.manual_seed(seed) # 设置CPU上的随机种子
    torch.cuda.manual_seed(seed) # 设置GPU上的随机种子
    torch.cuda.manual_seed_all(seed)  # 如果使用多GPU
    
    # 配置cuDNN以确保结果可重复
    if deterministic:
        torch.backends.cudnn.deterministic = True
        torch.backends.cudnn.benchmark = False


# 设置随机种子
set_seed(42)

（2）数据准备：生成合成的时间序列数据、标准化、数据划分

# 1-生成合成的时间序列数据
x = np.linspace(0,100,1000)
y = np.cos(x) + 0.1 * x + np.random.randn(1000) # 余弦波+线性趋势+噪声
# 可视化原始数据
plt.figure(figsize=(12, 6))
plt.plot(y)
plt.title('Sythesized Time Sequential Data (Cos + Linear + Noise)')
plt.xlabel('Seq_length')
plt.ylabel('Value')
plt.grid(True)
plt.show()

在这里需要注意的是顺序的选择：不能按照之前机器学习的思路，直接先划分训练集和测试集，然后滑动窗口得到数据对。这样做会导致数据不全。

因此需要先对全部的数据进行滑动窗口处理，然后再划分测试集和训练集。本质上讲，就是先转换为之前的模式（有结构化数据的数据对），然后划分数据集进行后续操作。

注：标准化时使用训练数据拟合，再转换整个数据。因为真实情况下，只知道历史数据的分布。

# 2-数据划分
train_size = int(len(y) * 0.8) # 训练集占比
train_data_raw = y[:train_size] # 得到训练集

# 2-1 标准化
# 缩放器处理特征矩阵，要求输入[样本数, 特征数]
scaler = MinMaxScaler(feature_range=(0,1))
scaler.fit(train_data_raw.reshape(-1,1)) # 学习训练集
scaled_y = scaler.transform(y.reshape(-1,1)).flatten() # 转换整个数据

# 2-2 定义生成数据对的函数（滑动窗口）
def create_sequences(data,seq_length):
    X,y = [],[] # 分别存储特征和标签
    for i in range(len(data)-seq_length):
        X.append(data[i:i+seq_length])
        y.append(data[i+seq_length])

    return np.array(X),np.array(y)

seq_length = 30
all_X,all_y = create_sequences(scaled_y,seq_length) # 得到数据对
# 2-3 划分测试集和训练集 
split_idx = train_size - seq_length

X_train = all_X[:split_idx]
y_train = all_y[:split_idx]
X_test = all_X[split_idx:]
y_test = all_y[split_idx:]

# 查看大小，验证
print("原始数据总长度:", len(y))
print("训练数据原始长度:", train_size)
print("测试数据原始长度:", len(y) - train_size)
print("-" * 30)
print("序列长度 (seq_length):", seq_length)
print("滑动窗口后样本总数:", len(all_X))
print("-" * 30)
print("训练集划分点 (split_idx):", split_idx)
print("训练集特征(X_train)形状:", X_train.shape) # (770, 30) -> (800-30, 30)
print("训练集标签(y_train)形状:", y_train.shape)   # (770,)
print("测试集特征(X_test)形状:", X_test.shape)   # (200, 30) -> (1000-30 - 770, 30)
print("测试集标签(y_test)形状:", y_test.shape)     # (200,)
print("-" * 30)

（3）调整形状

序列数据的形状：[samples,seq_length,features=1]（RNN）,对于传统机器学习模型的输入：[samples,features]。因此需要讲具有时间顺序的三维序列数据"扁平化"为二维特征表格，从而让传统的机器学习模型（如随机森林、SVM等）能够处理时间序列预测任务（牺牲时间性）。

# 3-调整形状，适配机器学习模型
# Scikit-learn的机器学习模型需要二维的输入: [样本数, 特征数]
# RNN需要的是三维输入: [样本数, 时间步长, 特征数]
# 我们需要将每个样本的 `seq_length` 个时间步“扁平化”成 `seq_length` 个特征。
# 原始形状: (770, 30, 1) or (770, 30) -> 目标形状: (770, 30)

X_train_rf = X_train.reshape(X_train.shape[0],-1)
X_test_rf = X_test.reshape(X_test.shape[0],-1)
# y_train,y_test形状符合要求

（4）搭建模型（RF）：训练、评估

按照之前的流程，核心的三行代码：实例化、训练、预测。

注：评估是要在原始尺度上（反标准化）比较，因为不同缩放的差异不同，与原始数据的误差也更具解释性。

# 4-模型
from sklearn.ensemble import RandomForestRegressor
from xgboost import XGBRegressor
from lightgbm import LGBMRegressor
rf_model = LGBMRegressor(random_state=42) # 实例化
rf_model.fit(X_train_rf,y_train) # 训练
# 得到训练集和测试集的预测结果
rf_train_pred = rf_model.predict(X_train_rf)
rf_test_pred = rf_model.predict(X_test_rf)

# 5-评估：RMSE
# 5-1 反标准化，在原始尺度上评估，scaler.inverse_transform 需要二维输入，所以先 reshape
rf_train_pred_origin = scaler.inverse_transform(rf_train_pred.reshape(-1,1))
rf_test_pred_origin = scaler.inverse_transform(rf_test_pred.reshape(-1,1))

y_train_origin = scaler.inverse_transform(y_train.reshape(-1,1))
y_test_origin = scaler.inverse_transform(y_test.reshape(-1,1))
    
# 5-2 计算RMSE
train_rmse = np.sqrt(mean_squared_error(y_train_origin,rf_train_pred_origin))
test_rmse = np.sqrt(mean_squared_error(y_test_origin,rf_test_pred_origin))
print(f"\n训练集 RMSE: {train_rmse:.4f}")
print(f"测试集 RMSE: {test_rmse:.4f}")

（5）可视化结果

绘制训练集和测试集的结果

注：原始数据和预测值存在时间偏移，需要先对齐，再绘图

# 可视化
plt.figure(figsize=(15, 7))
plt.plot(y, label='Origin', color='gray', alpha=0.5)

# 绘制训练集的预测结果
# 预测值与原始数据位置不同步（时间偏移），要对齐
train_predict_plot = np.empty_like(y) # 创建一个与原始数据y形状相同的空数组
train_predict_plot[:] = np.nan # 填充为空值，实现在有预测值的位置显示线条
train_predict_plot[seq_length : len(rf_train_pred_origin) + seq_length] = rf_train_pred_origin.flatten() #填入预测值
plt.plot(train_predict_plot, label='Train Pred (RF)', color='blue')

# 绘制测试集的预测结果
test_predict_plot = np.empty_like(y)
test_predict_plot[:] = np.nan
test_predict_plot[len(rf_train_pred_origin) + seq_length : len(y)] = rf_test_pred_origin.flatten()
plt.plot(test_predict_plot, label='Test Pred (RF)', color='red')

plt.title('Time Sequence Predictions(LGBM)')
plt.xlabel('Seq_length')
plt.ylabel('Value')
plt.legend()
plt.grid(True)
plt.show()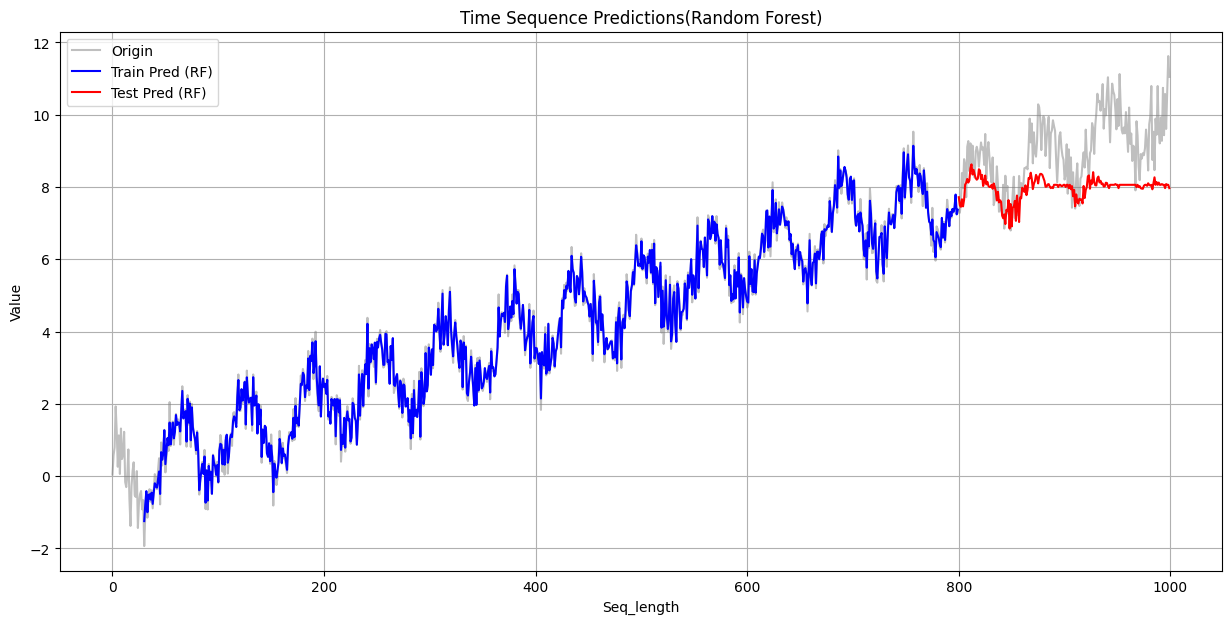

作业

使用数据：

x = np.linspace(0,100,1000)
y = np.cos(x) + 0.1 * x + np.random.randn(1000) # 余弦波+线性趋势+噪声

其余不变，查看各模型的输出：

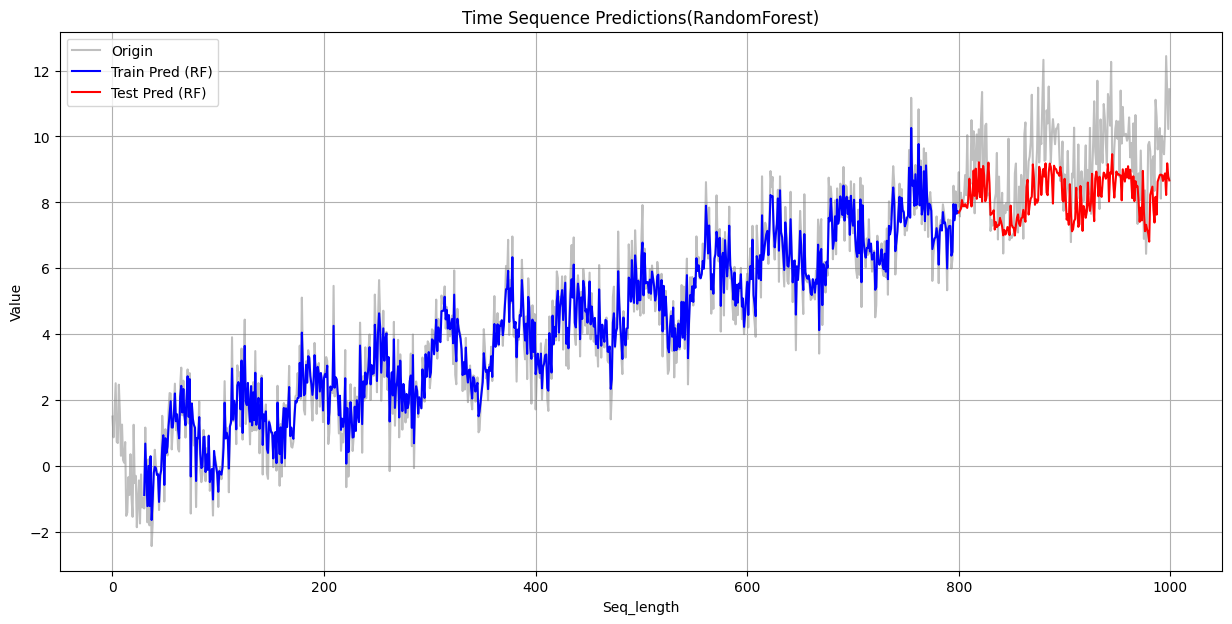
Random Forest

训练集 RMSE: 0.4269 测试集 RMSE: 1.4789

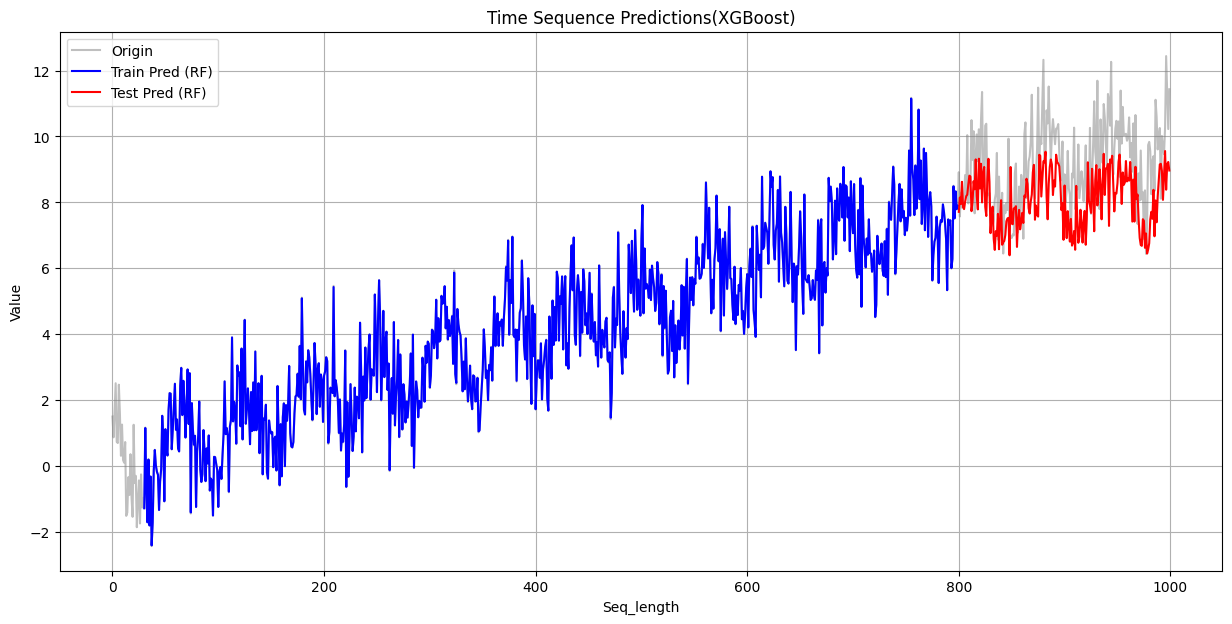
XGBoost

训练集 RMSE: 0.0110 测试集 RMSE: 1.5932

LGBM

训练集 RMSE: 0.1949 测试集 RMSE: 1.7703

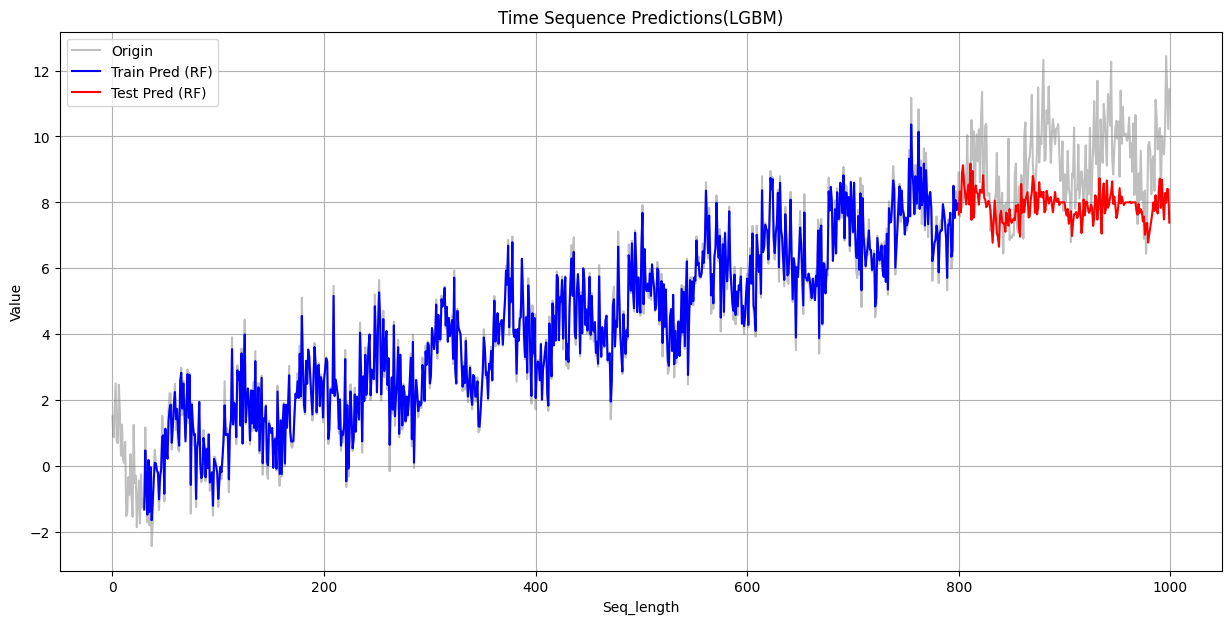
从上面可以看到，在训练集上，三个模型的表现都不错，其中XGBoost的误差最小，与原始数据重合度最高。但是在测试集上，三者的误差都比较大。

失败的原因根源在于决策树的工作原理：决策树及其集成模型（如随机森林）的预测基于训练数据的局部平均，其输出范围被训练集目标值的极值所严格限制，因此不具备外推能力，无法预测超出其“经验”范围的值。

模型（单棵树或森林）的最终预测值是训练样本在叶子节点内的平均值。
模型的预测结果严格限定在训练集目标值（y）的最小值与最大值之间。
模型学到的是输入与输出在训练集范围内的静态映射关系，而非抽象的、可延伸的“趋势”概念
当输入/输出超出训练范围时，模型只会给出其已知的边界极值，导致预测曲线变为一条水平线，无法进行有效外推。