games101 作业3

题目

1. 修改函数 rasterize_triangle(const Triangle& t) in rasterizer.cpp: 在此
   处实现与作业 2 类似的插值算法，实现法向量、颜色、纹理颜色的插值。
2. 修改函数 get_projection_matrix() in main.cpp: 将你自己在之前的实验中
   实现的投影矩阵填到此处，此时你可以运行 ./Rasterizer output.png normal
   来观察法向量实现结果。
3. 修改函数 phong_fragment_shader() in main.cpp: 实现 Blinn-Phong 模型计
   算 Fragment Color.
4. 修改函数 texture_fragment_shader() in main.cpp: 在实现 Blinn-Phong
   的基础上，将纹理颜色视为公式中的 kd，实现 Texture Shading Fragment
   Shader.
5. 修改函数 bump_fragment_shader() in main.cpp: 在实现 Blinn-Phong 的
   基础上，仔细阅读该函数中的注释，实现 Bump mapping.
6. 修改函数 displacement_fragment_shader() in main.cpp: 在实现 Bump
   mapping 的基础上，实现 displacement mapping.

题解

本次作业考察的技术点主要有3点：

1. 根据重心坐标进行插值，包括颜色插值、法向量插值、纹理坐标插值以及观 察坐标系中的顶点坐标插值。
2. Blinn-Phong 光照模型
3. 贴图，包括纹理贴图(texture)，凹凸贴图(bump)，位移贴图(displacement)

0.坐标转换回顾

在正式解题之前，我们先梳理一下顶点坐标以及法向量的转换过程。
模型坐标->（模型矩阵） 世界坐标->（观察矩阵）观察坐标->（投影矩阵）投影坐标->透视除法->（视口变换矩阵）屏幕坐标
(1). 获取模型坐标$pos$
(2). 计算世界坐标$po{s}_w=M_{model}\ast pos$
(其中$M_{model}$为模型变换矩阵：平移旋转缩放)
(3). 计算观察坐标$po{s}_v=M_{view}\ast M_{model}\ast pos$
(其中$M_{view}$为观察矩阵)
$$M_{\text{view }}=M_R\ast M_T$$
(4). 计算投影坐标$po{s}_p=M_{proj}\ast M_{view}\ast M_{model}\ast pos$
(其中$M_{proj}$为投影矩阵:正交投影或透视投影)
$$\begin{gathered} M_{\text{ortho }}=\left[\begin{array}{cccc}\frac{2}{r-l}& 0& 0& -\frac{r+l}{r-l}\\ 0& \frac{2}{t-b}& 0& -\frac{t+b}{t-b}\\ 0& 0& \frac{2}{n-f}& -\frac{n+f}{n-f}\\ 0& 0& 0& 1\end{array}\right] \\ {M}_{\text{persp }}=\left[\begin{array}{cccc}-\frac{1}{aspect\ast tan(\frac{fov}{2})}& 0& 0& 0\\ 0& -\frac{1}{tan(\frac{fov}{2})}& 0& 0\\ 0& 0& \frac{near+far}{near-far}& \frac{2\ast near\ast far}{near-far}\\ 0& 0& 1& 0\end{array}\right] \end{gathered}$$
(5). 透视除法$po{s}_h=po{s}_p/po{s}_p.w$
(6). 计算屏幕坐标$po{s}_{screen}=M_{viewport}\ast po{s}_h$
(其中$M_{viewport}$为视口变换矩阵)
$$M_{\text{viewport}}=\left[\begin{array}{cccc}\frac{w}{2}& 0& 0& \frac{w}{2}\\ 0& \frac{h}{2}& 0& \frac{h}{2}\\ 0& 0& 0& 0\\ 0& 0& 0& 1\end{array}\right]$$
其中$w,h$ 为视口的宽高
(7). 模型法向量转换
一般情况下，模型顶点转到世界坐标系，直接乘以模型矩阵即可，但是法向量是垂直某条边的，在进行xyz方向不等比缩放的情况下，原来的法向量则不垂直原来那条边。所以法向量的转换不能直接乘以模型矩阵。$n^{{}^{\prime }}=(M_{model}^{-1}{)}^T\ast n$. 详解参考博客。
如果是将模型法向量转为观察坐标系下的法向量，用于计算光照，则将上述的模型矩阵改为$M_{view}\ast M_{model}$就可以了。
假设模型法向量为$n$,观察坐标系下的法向量为$n_{view}=((M_{view}\ast M_{model}{)}^{-1}{)}^T\ast n$

(顶点的法向量计算：一个顶点作为多个三角形的公共顶点，此时，顶点法向量是相关三角形法向量的加权求和，权值为三角形的面积和所有相关三角形面积总和之比)

1. 插值

1. 计算重心坐标

在屏幕空间中，给定一个三角形的三个顶点（构成一个重心坐标系C），和一个任意点P，首先我们计算任意点P在重点坐标系C中的重心坐标。一般有两种计算方法：（1）几何面积法 (2) 坐标系角度法
重心坐标系满足以下两个条件：

因此，利用重心坐标系可以判断一个点是否位于三角形的内部。
根据前面介绍的两种方法，最终可以得出给定任一点 $P(x,y)$,和一个三角形$A(x_a,y_z),B(x_b,y_b),C(x_c,y_c)$,它的重心坐标为：
$$\begin{array}{rl}& \gamma =\frac{\left(y_a-y_b\right)x+\left(x_b-x_a\right)y+x_a{y}_b-x_b{y}_a}{\left(y_a-y_b\right)x_c+\left(x_b-x_a\right)y_c+x_a{y}_b-x_b{y}_a}\\ & \beta =\frac{\left(y_a-y_c\right)x+\left(x_c-x_a\right)y+x_a{y}_c-x_c{y}_a}{\left(y_a-y_c\right)x_b+\left(x_c-x_a\right)y_b+x_a{y}_c-x_c{y}_a}\\ & \alpha =1-\beta -\gamma \end{array}$$
代码如下

static std::tuple<float, float, float> computeBarycentric2D(float x, float y, const Vector4f* v){
    float c1 = (x*(v[1].y() - v[2].y()) + (v[2].x() - v[1].x())*y + v[1].x()*v[2].y() - v[2].x()*v[1].y()) / (v[0].x()*(v[1].y() - v[2].y()) + (v[2].x() - v[1].x())*v[0].y() + v[1].x()*v[2].y() - v[2].x()*v[1].y());
    float c2 = (x*(v[2].y() - v[0].y()) + (v[0].x() - v[2].x())*y + v[2].x()*v[0].y() - v[0].x()*v[2].y()) / (v[1].x()*(v[2].y() - v[0].y()) + (v[0].x() - v[2].x())*v[1].y() + v[2].x()*v[0].y() - v[0].x()*v[2].y());
    float c3 = (x*(v[0].y() - v[1].y()) + (v[1].x() - v[0].x())*y + v[0].x()*v[1].y() - v[1].x()*v[0].y()) / (v[2].x()*(v[0].y() - v[1].y()) + (v[1].x() - v[0].x())*v[2].y() + v[0].x()*v[1].y() - v[1].x()*v[0].y());
    return {c1,c2,c3};
}

2. 根据重心坐标插值

假设点$p(x,y,z)$在三角形$(A,B,C)$重心坐标为$(\alpha ,\beta ,\gamma )$,那么它的颜色插值$Colo{r}_p$,法线插值$Norma{l}_p$，纹理坐标插值$TexCoor{d}_p$分别为：
$$\begin{gathered} Colo{r}_p=\alpha \ast Colo{r}_A+\beta \ast Colo{r}_B+\gamma \ast Colo{r}_C \\ Norma{l}_p=\alpha \ast Norma{l}_A+\beta \ast Norma{l}_B+\gamma \ast Norma{l}_C \\ TexCoor{d}_p=\alpha \ast TexCoor{d}_A+\beta \ast TexCoor{d}_B+\gamma \ast TexCoor{d}_C \end{gathered}$$

2. 光照模型

目前为止，我了解到的光照模型：从宏观上分为两类：全局光照和局部光照。全局光照涉及到比如路径追踪，双向路径追踪，辐射方法等。局部光照包含我们经常接触到的：环境光照模型(Ambient)，漫反射光照模型(Lambert/Diffuse)，镜面光照模型（Phong），修正镜面光照模型（Blinn-Phong）和基于物理的光照模型（比如PBR等）。局部光照模型我理解的都是基于BRDF（双向反射分布函数）进行研究的，它的两大基础特性就是：（1）满足交换律（2）能量守恒。本文章仅整理一下Blinn-Phong模型的公式，因为它综合了环境光和漫反射光模型，并且对Phong模型进行了优化，至于基于物理的光照模型较为复杂，后续单独整理。

2.0 引个题

一个物体在场景中，能够被观察到，是因为它反射了某些光（假如它不能发光），这些光包含环境光，光源的光。（全局光照还得考虑其他物体反射的光）。而镜面光照模型认为（Phong）,反射到人眼的能量与入射光的角度、入射光的波长以及反射表面的材料性质有关，因此，观察到的光的强度就包含了三个主要信息：环境光，光源的光（漫反射光）和镜面反射光（高光）。

2.1 环境光

只考虑环境光的强度$I_a$和环境光的反射率$K_a$。（环境贴图就是使用贴图的采样值替换$I_a$）
$$I_{env}=K_a\ast I_a$$

2.2 漫反射光

光从光源出发，照射到物体表面的某个点上，该点会向周围各个方向进行反射光线，这种现象我们称之为漫反射。
物体表面的能量
假设场景中有个光源$L$，它距离物体的点$P$距离为$r$，那么点$P$接受到的能量
$$I^{{}^{\prime }}=I/r^2$$
该公式的推导如下：
假设有个一球体，球心有个光源，向四周发出能量，假设在单位球的表面，每个点的能量为$I$,那么单位球表面的能量就为$4\pi I$,根据能量守恒，在半径为$r$的同心圆表面（假设每个点的能量为$I^{{}^{\prime }}$）和单位圆表面的能量相等。那么：$4\pi r^2{I}^{{}^{\prime }}=4\pi I$,即$I^{{}^{\prime }}=I/r^2$

反射的能量
每个着色点对光的吸收率不一样（取决于光的颜色），我们用一个系数$K_d$表示该点的光的吸收率。（一般情况下用该点的颜色值或者纹理）

观察上图，入射角度越小，反射的能量越多，反射系数的范围【0，1】，刚好可以使用入射角度的余弦值表示$cos\theta =l\cdot n$ 。$l$为入射光线的单位向量，$n$为表面单位法向量 综上所述：漫反射光的公式如下：
$$L_d=K_d(I/r^2)max(0,l\cdot n)$$

2.3 高光

在物体表面的观察角度与光源角度正好是镜面对称时，即可看到高光.

如上图，向量$R$为反射光线，$V$为观察向量，两者越接近，高光越明显。
但是计算$R$的计算量较大，Blinn-Phong 提出了半程向量$h=normal(l+v)$

$h$和$n$的接近程度和$R$与$V$的接近程度相等。
物体表面某点的高光强度就可以用半程向量和法向量的夹角余弦表示：$cos\alpha =h\cdot n$
高光公式如下
$$L_s=K_s(I/r^2)max(0,h\cdot n{)}^p$$
其中$p$表示光的衰减系数，与物体的材质有关。表白越光滑的物体，$p$越大，衰减的速度会越快，高光点的范围越小，如下图：

Phong 光照模型为三种光照的相加
$$\begin{gathered} L=L_{env}+L_d+L_s \\ =K_a\ast I_a+K_d(I/r^2)max(0,l\cdot n)+K_s(I/r^2)max(0,h\cdot n{)}^p \end{gathered}$$
着色频率有三种类型：Flat shading(Face),Gouraud shading(vertex),Phong shading(pixel)

3. 贴图

贴图，顾名思义，就是将一张图片贴到物体表面。

1.纹理贴图

一般情况下，结合Phong 光照模型，将贴图采样后的颜色值设置为漫反射系数$K_{d}$ 即：
$$K_{d}=texture.sample(u,v)$$

纹理贴图会遇到两种问题：
1.Texture too small ：贴图的尺寸小于物体表面的尺寸，需要将贴图放大。此时可以进行双线性插值(此外还有近邻，三次样条插值)。

2.Texture too large ：贴图的尺寸比物体表面大，这种问题更难以处理，如果不处理会出现摩尔纹（一个texel的值代替了周围多个texel的值）。因为这种情况下，会出现贴图的多个texel,对应物体表面的一个像素pixel。采样后贴图时，很难查询多个texel的平均值，或者说一块纹素的综合值（这种查询我们称为范围查询）。解决这种问题，最著名的方式就是Mipmap
示意图如下：

空间小：所有层级的Mipmap所占用的存储空间只有原图的1/3
有了Mimap，我们如何做范围查找呢？如何知道屏幕上的一个像素去哪个层级的Mipmap查询，也就是如何确定一个像素和哪个层级的纹素是一一对应的？借用课件里面的图说明一下：

左边是屏幕种的像素，右图是源贴图中的纹素。通过计算像素的重心坐标，对纹理坐标进行插值后，会得到该像素点以及水平相邻点和垂直相邻点的纹理坐标（归一化的纹理坐标需要乘以纹理贴图的长和宽），如右图所示的红色点。计算水平相邻纹素的距离和垂直相邻纹素的距离最大值，然后取$lo{g}_2$，得到Mimpap的层级。此时还存在一个问题就是，层级都是整数，如果我们直接取整后从Mipmap取值，会出现“颜色断崖”现象，像这样：

此时可以利用线性插值，将D和D+1层的Mimap值进行插值计算，得到最终的颜色值。
当然，Mimap也有缺陷：只能矩形范围插值，对于长方形的纹理会出现过度模糊现象。此时可以使用各向异性过滤。

但是对于旋转的范围查找，课件中提供了一种方法：EWA过滤。（没太弄明白）

2.凹凸贴图（法线贴图）

使用一张纹理，存储每个纹素的“高度”信息，在每个像素纹理贴图时，采样纹理颜色值的同时，采样纹素的“高度”值。每个像素点本身有插值后的法向量$n$,我们通过该纹素周围的纹素的高度信息，能够计算出扰动后的法向量$n_{shift}$，最后通过$n_{shift}$进行光照模型计算。
![在这里插入图片描述](https://img-blog.csdnimg.cn/direct/b1c9b964cbc54afdab694c2779583468.png)

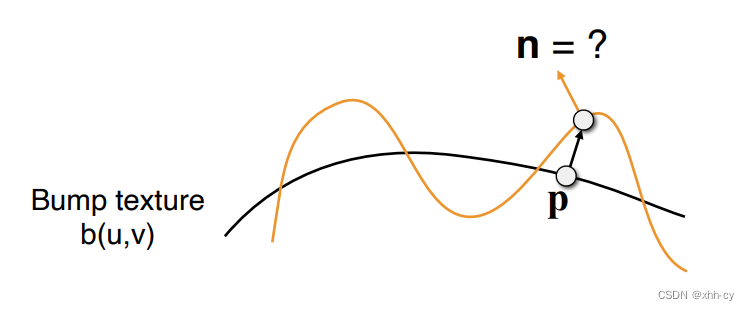
那么如何计算$n_{shift}$?
第一步：计算TBN矩阵
首先需要了解什么是切线空间，简单说，以表面点$p$为原点，法线N为z轴，然后在该点找一条切线T，垂直与法线N,然后再找一条副切线B,垂直N和T,由T B N构成的空间我们称之为切线空间。如下图：

TBN矩阵用于切线空间到其他空间的相互转换(这里的其他空间和N是在同一空间）。对于TBN矩阵的计算，网上大部分资料都在说通过几何坐标相对于纹理坐标的变化程度去计算，比如文章 ：凹凸贴图、法线贴图、切线空间、TBN矩阵讲解 文章：TBN都进行了详细的讲解，但是，对于作业中的T的计算，还是未能找打答案，不过，看了大佬的讲解，终于明白了，以下是我的个人理解和推导。
我们确定一个z轴方向就是法线$N(x,y,z)$,然后我们计算x轴方向，也就是切线方向T(tangent)。
最后通过N和T的叉乘得到副切线向量B(bitangent),下面是具体的步骤：

1.将法向量投影到$xoz$平面，得到$n_{xz}=(x,0,z)$,$|n_{xz}|=\sqrt{x^2+z^2}$
2.旋转向量$n_{xz}$和y轴正向重合，得到$n_{xz}^{{}^{\prime }}$,记为$t_y=(0,\sqrt{x^2+z^2},0)$
3.$n_y和n_{xz}$做同样的旋转得到$n_y^{{}^{\prime }}$,$n_y^{{}^{\prime }}$将会落到$xoz$平面。
4.根据下图中的手动推导，可以计算$n_y^{{}^{\prime }}=(t_x,0,t_z)$
5.因为旋转了90度，$t_x$和t_{z}分别和$x,z$是反向的，所以前面需要加负号。（作业里面的示例代码有问题)
6.最后得到T $$T=(-xy/\sqrt{x^2+z^2},\sqrt{x^2+z^2},-zy/\sqrt{x^2+z^2})$$可以通过点乘验证T和N垂直。其实T就是N旋转90度后得到向量。而围绕的旋转轴就是$R=N\times n_{xz}=(yz,0,-xy)$,根据三维向量围绕任意轴的旋转矩阵，也可以得到T(方向可能和前一种方式得到的相反，但这并不影响切线空间的构建)
$$T=(xy/\sqrt{x^2+z^2},-\sqrt{x^2+z^2},zy/\sqrt{x^2+z^2})$$
7.最后通过N和T的叉乘，就可以得到B.$$B=N\times T$$

第二步 扰动法向量
这一步的计算必须是在切线空间中计算，根据高度图，计算扰动的法线（切线空间中）。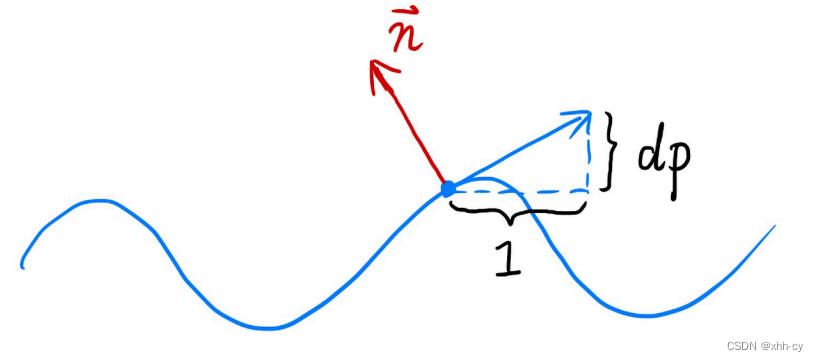

1）求这一点的几何坐标相对于高度信息的偏导数，得到切线向量（如课件所示）。
2）根据切线和法线垂直，得到法向量$N_{tbn}$（如课件所示）。
3）最后乘以矩阵$TBN$,得到扰动的法向量$N_{perturb}$。
$$N_{perturb}=N_{tbn}\ast TBN$$
第三步 根据扰动后的法线，进行Phong 光照计算。

3.位移贴图

弄明白凹凸贴图，就很容易理解位移贴图了，位移贴图就是根据高度图，沿着扰动后的法线方向移动顶点的位置，而不仅仅是扰动法线了。具体的步骤如下：
1.计算TBN矩阵。
2.扰动法向量。（同凹凸贴图）
3.获取高度信息，记为$huv$。
4.原始顶点沿着扰动后的法线方向移动$huv$的距离，得到新的顶点坐标。

位移贴图比凹凸贴图更加真实。

本次作业的答案放在的git仓库中：作业地址