前往我的博客阅读体验更佳:本文链接
3 雅可比矩阵
3.1 概念
由正运动学分析可知,只要我们知道机器人的结构以及每个关节的位置(旋转关节的角度或者移动关节的平移),就可以求出末端执行器的位姿,即末端执行器的位姿和关节位置有如下关系:
x
⃗
=
f
(
θ
⃗
)
(1)
\vec{x}=f(\vec\theta)\tag{1}
x=f(θ)(1)
其中,
x
⃗
\vec x
x表示末端执行器的位姿,
θ
⃗
\vec\theta
θ表示关节角度。
对式(1)两边同时对时间
t
t
t求导可得:
d
x
⃗
d
t
=
d
f
(
θ
⃗
)
d
t
=
d
f
(
θ
⃗
)
d
θ
⃗
⋅
d
θ
⃗
d
t
(2)
\frac{\mathrm d\vec x}{\mathrm d t}=\frac{\mathrm df(\vec \theta)}{\mathrm dt}=\frac{\mathrm df( \vec\theta)}{\mathrm d\vec\theta}·\frac{\mathrm d\vec\theta}{\mathrm dt}\tag{2}
dtdx=dtdf(θ)=dθdf(θ)⋅dtdθ(2)
即:
x
˙
=
d
x
⃗
d
θ
⃗
⋅
θ
˙
=
J
(
θ
)
⋅
θ
˙
(3)
\dot x=\frac{\mathrm d\vec x}{\mathrm d\vec\theta}·\dot\theta=J(\theta)·\dot\theta\tag{3}
x˙=dθdx⋅θ˙=J(θ)⋅θ˙(3)
矩阵 J ( θ ) J(\theta) J(θ)即为机器人的雅可比矩阵,它将机器人关节空间的速度与操作空间的速度联系起来。这里需要注意 x ⃗ \vec{x} x, x ⃗ \vec{x} x的描述有多种形式,其位置和姿态可以表示在笛卡尔坐标系、柱坐标系、球坐标系等不同坐标系下,其姿态可以表示为欧拉角、四元数等等。随着 x ⃗ \vec{x} x的描述不同,雅可比矩阵 J ( θ ) J(\theta) J(θ)也会随之变化。为方便起见,定义基本雅可比矩阵,即用笛卡尔坐标描述线速度和角速度、以机械臂的基准坐标系(即坐标系 { 0 } \{0\} {0})作为参照系来描述末端执行器速度所求得的雅可比矩阵。(如无特殊说明,以下提到的雅可比矩阵均指基本雅可比矩阵)
3.2 UR3基本雅可比矩阵的求解
根据基本雅可比矩阵的定义,末端执行器的速度可以写为:
x
˙
=
[
v
x
v
y
v
z
ω
x
ω
y
ω
z
]
=
[
v
⃗
ω
⃗
]
(4)
\dot x= \begin{bmatrix} v_x \\v_y\\v_z\\\omega_x\\\omega_y\\\omega_z \end{bmatrix} = \begin{bmatrix} \vec v \\\vec \omega \end{bmatrix}\tag{4}
x˙=⎣⎢⎢⎢⎢⎢⎢⎡vxvyvzωxωyωz⎦⎥⎥⎥⎥⎥⎥⎤=[vω](4)
雅可比矩阵应为
6
∗
6
6*6
6∗6的矩阵,可以写成:
J
=
[
J
v
J
ω
]
(5)
J= \begin{bmatrix} J_v \\J_\omega \end{bmatrix}\tag{5}
J=[JvJω](5)
上半部分对应线速度,下半部分对应角速度。
3.2.1 线速度部分
由正运动学部分可以得到,末端执行器位姿矩阵为:
T
6
0
=
[
n
x
o
x
a
x
p
x
n
y
o
y
a
y
p
y
n
z
o
z
a
z
p
z
0
0
0
1
]
(6)
T^0_6 = \begin{bmatrix} n_x & o_x & a_x & p_x \\ n_y & o_y & a_y & p_y \\ n_z & o_z & a_z & p_z \\ 0 & 0 & 0 & 1 \end{bmatrix}\tag{6}
T60=⎣⎢⎢⎡nxnynz0oxoyoz0axayaz0pxpypz1⎦⎥⎥⎤(6)
其中
p
x
p_x
px、
p
y
p_y
py、
p
z
p_z
pz即为末端执行器在坐标系
{
0
}
\{0\}
{0}下的位置,因此,要求雅可比矩阵线速度部分
J
v
J_v
Jv,只需要将
p
x
p_x
px、
p
y
p_y
py、
p
z
p_z
pz分别对关节角求导即可。所以,可求得
J
v
J_v
Jv为:
J
v
=
[
d
p
x
d
θ
1
d
p
x
d
θ
2
d
p
x
d
θ
3
d
p
x
d
θ
4
d
p
x
d
θ
5
d
p
x
d
θ
6
d
p
y
d
θ
1
d
p
y
d
θ
2
d
p
y
d
θ
3
d
p
y
d
θ
4
d
p
y
d
θ
5
d
p
y
d
θ
6
d
p
z
d
θ
1
d
p
z
d
θ
2
d
p
z
d
θ
3
d
p
z
d
θ
4
d
p
z
d
θ
5
d
p
z
d
θ
6
]
(7)
J_v= \begin{bmatrix} \frac{\mathrm{d}p_x}{\mathrm{d}\theta_1} & \frac{\mathrm{d}p_x}{\mathrm{d}\theta_2} & \frac{\mathrm{d}p_x}{\mathrm{d}\theta_3} & \frac{\mathrm{d}p_x}{\mathrm{d}\theta_4} & \frac{\mathrm{d}p_x}{\mathrm{d}\theta_5} & \frac{\mathrm{d}p_x}{\mathrm{d}\theta_6} \\ \frac{\mathrm{d}p_y}{\mathrm{d}\theta_1} & \frac{\mathrm{d}p_y}{\mathrm{d}\theta_2} & \frac{\mathrm{d}p_y}{\mathrm{d}\theta_3} & \frac{\mathrm{d}p_y}{\mathrm{d}\theta_4} & \frac{\mathrm{d}p_y}{\mathrm{d}\theta_5} & \frac{\mathrm{d}p_y}{\mathrm{d}\theta_6} \\ \frac{\mathrm{d}p_z}{\mathrm{d}\theta_1} & \frac{\mathrm{d}p_z}{\mathrm{d}\theta_2} & \frac{\mathrm{d}p_z}{\mathrm{d}\theta_3} & \frac{\mathrm{d}p_z}{\mathrm{d}\theta_4} & \frac{\mathrm{d}p_z}{\mathrm{d}\theta_5} & \frac{\mathrm{d}p_z}{\mathrm{d}\theta_6} \end{bmatrix}\tag{7}
Jv=⎣⎢⎡dθ1dpxdθ1dpydθ1dpzdθ2dpxdθ2dpydθ2dpzdθ3dpxdθ3dpydθ3dpzdθ4dpxdθ4dpydθ4dpzdθ5dpxdθ5dpydθ5dpzdθ6dpxdθ6dpydθ6dpz⎦⎥⎤(7)
3.2.2 角速度部分
在三维空间里,角速度定义为一个指向旋转轴的向量,其方向可以由右手定则确定。因为我们定义机械臂的每个旋转关节都是绕自身的z轴旋转的,所以当一个旋转关节转速为 ω \omega ω时,它所贡献的的末端执行器的角速度向量以这个旋转关节本身的坐标系为参照系必然为 [ 0 , 0 , ω ] [0,0,\omega] [0,0,ω]。换句话说,这个旋转关节的转速乘以 [ 0 , 0 , 1 ] [0, 0, 1] [0,0,1]即可得到它所引起的末端执行器的角速度(在该旋转关节坐标系下)。末端执行器的实际转速可由不同旋转关节贡献的的角速度线性叠加得到。
由于我们的基本雅可比矩阵是以坐标系 { 0 } \{0\} {0}为参照系的,为了写出 J ω J_\omega Jω,我们需要把每个旋转关节的 z z z轴 [ 0 , 0 , 1 ] [0, 0, 1] [0,0,1],从以关节自身坐标系为参照系转换到基准坐标系 { 0 } \{0\} {0}中表示。另外,对于平移关节,因为平移关节的运动不可能改变末端执行器的朝向,所以末端执行器的角速度对平移关节位置的求导一定是0!
所以,雅可比矩阵角速度部分
J
ω
J_\omega
Jω为:
J
ω
=
[
0
Z
^
1
0
Z
^
2
0
Z
^
3
0
Z
^
4
0
Z
^
5
0
Z
^
6
]
(8)
J_\omega= \begin{bmatrix} ^0\hat{Z}_1 & ^0\hat{Z}_2 & ^0\hat{Z}_3 & ^0\hat{Z}_4 & ^0\hat{Z}_5 & ^0\hat{Z}_6 \end{bmatrix}\tag{8}
Jω=[0Z^10Z^20Z^30Z^40Z^50Z^6](8)
由正运动学部分分析可知,
0
Z
^
i
^0\hat{Z}_i
0Z^i即为齐次坐标矩阵
T
i
0
T^0_i
Ti0第三列前三行元素。
3.2.3 UR3机器人雅可比矩阵解析表达式
由正运动学部分可知
{
p
x
=
(
s
1
c
5
−
c
1
c
234
s
5
)
d
6
+
c
1
s
234
d
5
+
c
1
c
23
a
3
+
s
1
d
4
+
c
1
c
2
a
2
+
s
1
d
2
p
y
=
−
(
c
1
c
5
+
s
1
c
234
s
5
)
d
6
+
s
1
s
234
d
5
+
s
1
c
23
a
3
−
c
1
d
4
+
s
1
c
2
a
2
−
c
1
d
2
p
z
=
−
s
234
s
5
d
6
−
c
234
d
5
+
s
23
a
3
+
s
2
a
2
+
d
1
(9)
\left\{ \begin{array}{lr} p_x = (s_1c_5-c_1c_{234}s_5)d_6+c_1s_{234}d_5+c_1c_{23}a_3+s_1d_4+c_1c_2a_2+s_1d_2 \\ p_y = -(c_1c_5+s_1c_{234}s_5)d_6+s_1s_{234}d_5+s_1c_{23}a_3-c_1d_4+s_1c_2a_2-c_1d_2 \\ p_z = -s_{234}s_5d_6-c_{234}d_5+s_{23}a_3+s_2a_2+d_1 \end{array} \right.\tag{9}
⎩⎨⎧px=(s1c5−c1c234s5)d6+c1s234d5+c1c23a3+s1d4+c1c2a2+s1d2py=−(c1c5+s1c234s5)d6+s1s234d5+s1c23a3−c1d4+s1c2a2−c1d2pz=−s234s5d6−c234d5+s23a3+s2a2+d1(9)
T
1
0
=
[
∗
∗
0
∗
∗
∗
0
∗
∗
∗
1
∗
0
0
0
1
]
(10)
T^0_1= \begin{bmatrix} * & * & 0 & * \\ * & * & 0 & * \\ * & * & 1 & * \\ 0 & 0 & 0 & 1 \end{bmatrix}\tag{10}
T10=⎣⎢⎢⎡∗∗∗0∗∗∗00010∗∗∗1⎦⎥⎥⎤(10)
T
2
0
=
[
∗
∗
s
1
∗
∗
∗
−
c
1
∗
∗
∗
0
∗
0
0
0
1
]
(11)
T^0_2= \begin{bmatrix} * & * & s_1 & * \\ * & * & -c_1 & * \\ * & * & 0 & * \\ 0 & 0 & 0 & 1 \end{bmatrix}\tag{11}
T20=⎣⎢⎢⎡∗∗∗0∗∗∗0s1−c100∗∗∗1⎦⎥⎥⎤(11)
T
3
0
=
[
∗
∗
s
1
∗
∗
∗
−
c
1
∗
∗
∗
0
∗
0
0
0
1
]
(12)
T^0_3= \begin{bmatrix} * & * & s_1 & * \\ * & * & -c_1 & * \\ * & * & 0 & * \\ 0 & 0 & 0 & 1 \end{bmatrix}\tag{12}
T30=⎣⎢⎢⎡∗∗∗0∗∗∗0s1−c100∗∗∗1⎦⎥⎥⎤(12)
T
4
0
=
[
∗
∗
s
1
∗
∗
∗
−
c
1
∗
∗
∗
0
∗
0
0
0
1
]
(13)
T^0_4= \begin{bmatrix} * & * & s_1 & * \\ * & * & -c_1 & * \\ * & * & 0 & * \\ 0 & 0 & 0 & 1 \end{bmatrix}\tag{13}
T40=⎣⎢⎢⎡∗∗∗0∗∗∗0s1−c100∗∗∗1⎦⎥⎥⎤(13)
T
5
0
=
[
∗
∗
c
1
s
234
∗
∗
∗
s
1
s
234
∗
∗
∗
−
c
234
∗
0
0
0
1
]
(14)
T^0_5= \begin{bmatrix} * & * & c_1s_{234} & * \\ * & * & s_1s_{234} & * \\ * & * & -c_{234} & * \\ 0 & 0 & 0 & 1 \end{bmatrix}\tag{14}
T50=⎣⎢⎢⎡∗∗∗0∗∗∗0c1s234s1s234−c2340∗∗∗1⎦⎥⎥⎤(14)
T
6
0
=
[
∗
∗
s
1
c
5
−
c
1
c
234
s
5
∗
∗
∗
−
c
1
c
5
−
s
1
c
234
s
5
∗
∗
∗
−
s
234
s
5
∗
0
0
0
1
]
(15)
T^0_6= \begin{bmatrix} * & * & s_1c_5-c_1c_{234}s_5 & * \\ * & * & -c_1c_5-s_1c_{234}s_5 & * \\ * & * & -s_{234}s_5 & * \\ 0 & 0 & 0 & 1 \end{bmatrix}\tag{15}
T60=⎣⎢⎢⎡∗∗∗0∗∗∗0s1c5−c1c234s5−c1c5−s1c234s5−s234s50∗∗∗1⎦⎥⎥⎤(15)
所以,UR3机器人的雅可比矩阵为:
J
=
[
j
11
j
12
j
13
j
14
j
15
0
j
21
j
22
j
23
j
24
j
25
0
0
j
32
j
33
j
34
j
35
0
0
s
1
s
1
s
1
c
1
s
234
j
46
0
−
c
1
−
c
1
−
c
1
s
1
s
234
j
56
1
0
0
0
−
c
234
j
66
]
(16)
% J = % \begin{bmatrix} % j_{11} & j_{12} & j_{13} & j_{14} & j_{15} & j_{16} \\ % j_{21} & j_{22} & j_{23} & j_{24} & j_{25} & j_{26} \\ % j_{31} & j_{32} & j_{33} & j_{34} & j_{35} & j_{36} \\ % j_{41} & j_{42} & j_{43} & j_{44} & j_{45} & j_{46} \\ % j_{51} & j_{52} & j_{53} & j_{54} & j_{55} & j_{56} \\ % j_{61} & j_{62} & j_{63} & j_{64} & j_{65} & j_{66} % \end{bmatrix} J = \begin{bmatrix} j_{11} & j_{12} & j_{13} & j_{14} & j_{15} & 0 \\ j_{21} & j_{22} & j_{23} & j_{24} & j_{25} & 0 \\ 0 & j_{32} & j_{33} & j_{34} & j_{35} & 0 \\ 0 & s_1 & s_1 & s_1 & c_1s_{234} & j_{46} \\ 0 & -c_1 & -c_1 & -c_1 & s_1s_{234} & j_{56} \\ 1 & 0 & 0 & 0 & -c_{234} & j_{66} \end{bmatrix}\tag{16}
J=⎣⎢⎢⎢⎢⎢⎢⎡j11j210001j12j22j32s1−c10j13j23j33s1−c10j14j24j34s1−c10j15j25j35c1s234s1s234−c234000j46j56j66⎦⎥⎥⎥⎥⎥⎥⎤(16)
式(16)中各简式如下:
{
j
11
=
(
c
1
c
5
+
s
1
c
234
s
5
)
d
6
−
s
1
s
234
d
5
−
s
1
c
23
a
3
+
c
1
d
4
−
s
1
c
2
a
2
+
c
1
d
2
j
21
=
(
s
1
c
5
−
c
1
c
234
s
5
)
d
6
+
c
1
s
234
d
5
+
c
1
c
23
a
3
+
s
1
d
4
+
c
1
c
2
a
2
+
s
1
d
2
j
12
=
−
c
1
(
−
s
234
s
5
d
6
−
c
234
d
5
+
s
23
a
3
+
s
2
a
2
)
j
22
=
−
s
1
(
−
s
234
s
5
d
6
−
c
234
d
5
+
s
23
a
3
+
s
2
a
2
)
j
32
=
−
c
234
s
5
d
6
+
s
234
d
5
+
c
23
a
3
+
c
2
a
2
j
13
=
c
1
(
s
234
s
5
d
6
+
c
234
d
5
−
s
23
a
3
)
j
23
=
s
1
(
s
234
s
5
d
6
+
c
234
d
5
−
s
23
a
3
)
j
33
=
−
c
234
s
5
d
6
+
s
234
d
5
+
c
23
a
3
j
14
=
c
1
(
s
234
s
5
d
6
+
c
234
d
5
)
j
24
=
s
1
(
s
234
s
5
d
6
+
c
234
d
5
)
j
34
=
−
c
234
s
5
d
6
+
s
234
d
5
j
15
=
−
(
s
1
s
5
+
c
1
c
234
c
5
)
d
6
j
25
=
(
c
1
s
5
−
s
1
c
234
c
5
)
d
6
j
35
=
−
s
234
c
5
d
6
j
46
=
s
1
c
5
−
c
1
c
234
s
5
j
56
=
−
c
1
c
5
−
s
1
c
234
s
5
j
66
=
−
s
234
s
5
(17)
\left\{ \begin{array}{lr} j_{11}=(c_1c_5+s_1c_{234}s_5)d_6-s_1s_{234}d_5-s_1c_{23}a_3+c_1d_4-s_1c_2a_2+c_1d_2 \\ j_{21}=(s_1c_5-c_1c_{234}s_5)d_6+c_1s_{234}d_5+c_1c_{23}a_3+s_1d_4+c_1c_2a_2+s_1d_2 j_{12}=-c_1(-s_{234}s_5d_6-c_{234}d_5+s_{23}a_3+s_2a_2) \\ j_{22}=-s_1(-s_{234}s_5d_6-c_{234}d_5+s_{23}a_3+s_2a_2) \\ j_{32}=-c_{234}s_5d_6+s_{234}d_5+c_{23}a_3+c_2a_2 j_{13}=c_1(s_{234}s_5d_6+c_{234}d_5-s_{23}a_3) \\ j_{23}=s_1(s_{234}s_5d_6+c_{234}d_5-s_{23}a_3) \\ j_{33}=-c_{234}s_5d_6+s_{234}d_5+c_{23}a_3 j_{14}=c_1(s_{234}s_5d_6+c_{234}d_5) \\ j_{24}=s_1(s_{234}s_5d_6+c_{234}d_5) \\ j_{34}=-c_{234}s_5d_6+s_{234}d_5 j_{15}=-(s_1s_5+c_1c_{234}c_5)d_6 \\ j_{25}=(c_1s_5-s_1c_{234}c_5)d_6 \\ j_{35}=-s_{234}c_5d_6 j_{46}=s_1c_5-c_1c_{234}s_5 \\ j_{56}=-c_1c_5-s_1c_{234}s_5 \\ j_{66}=-s_{234}s_5 \\ \end{array} \right.\tag{17}
⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧j11=(c1c5+s1c234s5)d6−s1s234d5−s1c23a3+c1d4−s1c2a2+c1d2j21=(s1c5−c1c234s5)d6+c1s234d5+c1c23a3+s1d4+c1c2a2+s1d2j12=−c1(−s234s5d6−c234d5+s23a3+s2a2)j22=−s1(−s234s5d6−c234d5+s23a3+s2a2)j32=−c234s5d6+s234d5+c23a3+c2a2j13=c1(s234s5d6+c234d5−s23a3)j23=s1(s234s5d6+c234d5−s23a3)j33=−c234s5d6+s234d5+c23a3j14=c1(s234s5d6+c234d5)j24=s1(s234s5d6+c234d5)j34=−c234s5d6+s234d5j15=−(s1s5+c1c234c5)d6j25=(c1s5−s1c234c5)d6j35=−s234c5d6j46=s1c5−c1c234s5j56=−c1c5−s1c234s5j66=−s234s5(17)
3.3 验证
利用Robotics Toolbox进行验证,当关节角为 Θ = [ 1 5 ∘ 1 5 ∘ 1 5 ∘ 1 5 ∘ 1 5 ∘ 1 5 ∘ ] T \Theta=\left[15^{\circ}\ 15^{\circ}\ 15^{\circ}\ 15^{\circ}\ 15^{\circ}\ 15^{\circ}\right]^T Θ=[15∘ 15∘ 15∘ 15∘ 15∘ 15∘]T时,分别利用Robotics Toolbox中R.jacob0()函数以及自己编写函数进行求解,所得结果如下图所示:
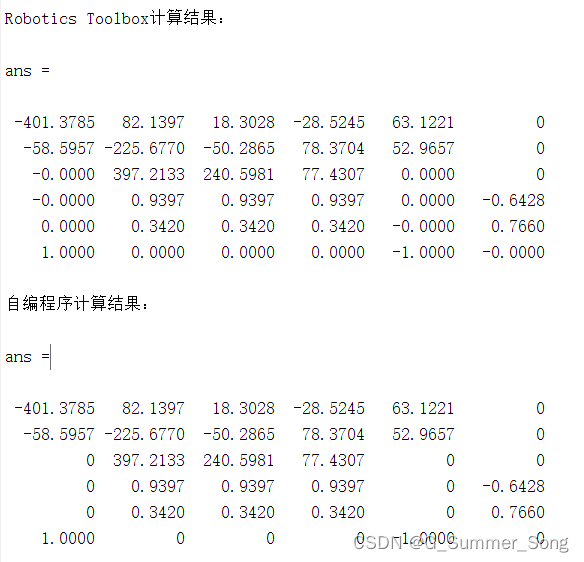
从图中可以看出,利用Robotics Toolbox中R.jacob0()函数和自编函数计算结果相同,说明3.2.3节中雅可比矩阵解析表达式求解无误。





















 2400
2400

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








