深度学习笔记:正则化和批量归一化

原创于 2025-11-17 15:01:24 发布 · 758 阅读

20 ·

CC 4.0 BY-SA版权

文章标签：

#深度学习 #笔记 #人工智能

部署运行你感兴趣的模型镜像

正则化为了防止模型过拟合的一种操作，那么什么是过拟合。

过拟合就是说在模型训练中，学习了许多无关紧要的东西或者是学习了错误的规律，比如在预测房价的训练中，模型居然把门前有几朵花这种类似的特征都学习进去了，又或者在识别猫狗的训练中，模型并不是通过猫狗的生物特征，而是通过背景板来判断是猫是狗，类似的情况都称作为过拟合。

根本原因：模型复杂度过高，学习了训练数据中的噪声和偶然模式

核心矛盾：降低了训练误差，但提高了测试误差，即泛化能力下降。

那么正则化就是针对于上述情况的一种策略，那么又应该如何防止模型这种错误的特征学习呢？我认为本质上就是权重的更新上入手，那么下文就是一些正则化的手段。

L1，L2正则化

L1，L2正则化，又叫做范数惩罚，他是通过在损失函数中添加模型参数的范数作为惩罚项，来到到防止过拟合的效果。

公式

$L1=loss+\lambda *||w||$

$||w||=\sum_{i}^{} |w_i|$

$L2=loss+(\lambda/2) *||w||_2^2$

$||w||_2^2=(\sqrt[2]{\sum_{i}^{}w_i^2})^2=\sum_{i}^{}w_i^2$

以上就是范数惩罚的公式

梯度更新

对于L1正则化，||w||的求导可以看做大于0的取1，小于0的取-1，等于0就取0也就是sign函数，那么在梯度更新中(此处就以SGD举例)就长这样

$w'=w-lr*(\partial L/\partial w+\lambda *sign(w))$

不难发现，这样在参数更新中，都会多减去一个固定量（λ * sign(w)），对于参数本身较小的值，这个固定量影响就更大，本身参数较大的值这个固定量的影响就小，循环往复后，那些参数小的值就会在0附近震荡，在实践中就直接变为0。

那对于L2正则化，(||w||_2)^2的求导就等于当前参数的w，也就是

$w'=w-lr*(\partial L/\partial w+\lambda *w)=(1-lr *\lambda)*w-lr*(\partial L/\partial w)$

每次更新时，权重都会先乘以 (1 - lr*λ)，然后再减去原始梯度，这样每次更新，参数都会一点点向0收缩，但永不为0（因为w_n的系数是指数衰减的）。

直观理解

对此我们可以这么理解L1，L2正则化

L1正则化是通过把并非重要的参数直接变为0，就像一个老师让你把那些不重要的科目废弃，只去学重要的，以此达到重要特征学习正确的效果；

L2正则化是通过保留所有特征，但是都在缓慢下降的策略，就像一个老师让你学所有科目，但是所有时间都平均下来，到达一个不会过度关注不重要特征的效果。

代码演示

pytorch中演示L2正则化，L1要手动实现

import torch
import torch.nn as nn
import torch.optim as optim
# 设定w
w=torch.tensor([1.0],requires_grad=True,dtype=torch.float)
# 定义损失函数
criterion = ((w ** 2) / 2.0)
# 优化器 
optimizer = optim.SGD(params=[w], lr=0.01, weight_decay=0.01) # weight_decay=惩罚力度
# 清空梯度，避免累加
optimizer.zero_grad()
# 反向传播，计算梯度
criterion.backward()
# 梯度下降 参数更新
optimizer.step()

print(w.grad)
#模拟第二次
criterion = ((w ** 2) / 2.0)
optimizer.zero_grad()
criterion.backward()
optimizer.step()
print(w.grad)

Dropout正则化

核心思路

Dropout的思路和L1，L2有所不同，L1，L2正则化是通过惩罚权重来达到防止过拟合的效果，而Dropout的核心思路是，在训练过程中随机丢弃部分神经元，破坏了神经网络固有的连接，强制每个神经元都有独立发挥的可能，而不是过度依赖某几个神经元（万一那几个神经元理解的特征是错误的或不重要的呢）。

代码演示

在训练过程中，Dropout的实现是让神经元以超参数p的概率停止工作或者激活被置为0,未被置为0的进行缩放，缩放比例为1/(1-p)（为了保证最终的输出期望一样）。训练过程可以认为是对完整的神经网络的一些子集进行训练，每次基于输入数据只更新子网络的参数。

在测试过程中，随机失活不起作用。

import torch
import torch.nn as nn
import torch.optim as optim

# 输入
x=torch.randint(0,10,(1,4),dtype=torch.float)
print(x)
# 线性层
linear1=nn.Linear(4,5)
y=linear1(x)
print(y)
# 激活函数
output=torch.relu(y)
print(output)
# dropout层，对上一层的输出随机归零(失活)
dropout=nn.Dropout(p=0.5)
d1=dropout(output)
print(d1)

批量归一化（Batch Normalization）

该操作通常在激活函数之前，加权求和之后。

问题的根源

对于一个神经网络，每个神经元都会对上一层的输出进行一个加权求和，那么我们可以假象一下，如果第一层他的输出是[1,0,2]，第二次会对这些数据进行加权求和，而第二层的输出是[1000,1203,1230]，第三层会对这些数据进行处理，那么每一层所处理的数据的范围波动太大，这会导致网络每次迭代过程都要去适应不同分布的数据，学习效率变低。

因此会出现以下几个问题:
1.针对不同的的输出范围，需要的学习率不一样。

2.对于输出太大的值，激活函数容易饱和，梯度会消失。

3.内部每层的输出分布每次变化太大，会导致后面所有层连锁大幅度变化，从而无法关注正确的特征分布。

公式

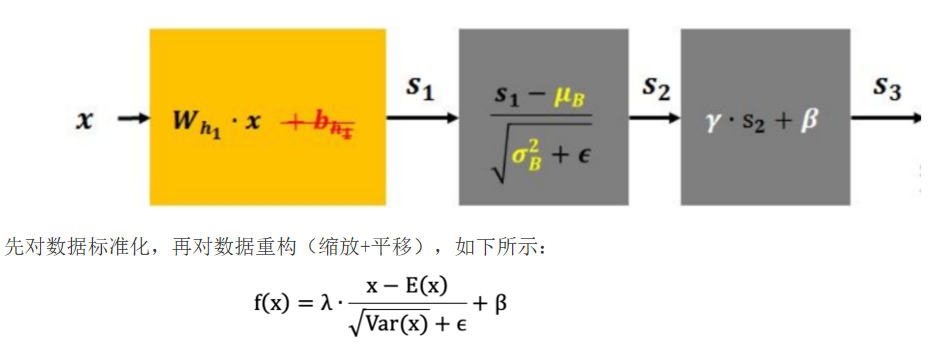
批量归一化的操作就是基于小批量数据，先做了一个标准化，E(x)是均值，Var(x)是方差，图中s1后面的步骤就是标准化，他的作用是把任意分布的数据都拉回到一个以0为中心点，向外扩散的分布中，也就是标准正态分布N(0,1)，然后就是缩放和平移，γ和β都是可以学习的参数，s2后面的就是，网络会学习最合适的分布，会把标准化后的分布缩放位移到N(β, γ²)分布上。

思考与正则化的关系

那么BN是是否有正则化的效果呢？答案是有的，相较于Dropout的随机关闭神经元和L1L2正则化的惩罚机制，他是通过噪声注入的方法实现归一化的。

这里的噪声就是指BN的统计量波动，导致破坏了原有模型对特定路径依赖，从而防止了过拟合的情况，这点和Dropout有点像。

代码

import torch
import torch.nn as nn
# 1. 创建图像样本数据.
# 1张图片, 2个通道, 3行4列(像素点)
input_2d = torch.randn(size=(1, 2, 3, 4))
print(f'input_2d: {input_2d}')

# 2. 创建批量归一化层(BN层)
# 参1: 输入特征数 = 图片的通道数.
# 参2: 噪声值(小常数), 默认为1e-5.
# 参3: 动量值, 用于计算移动平局统计量的  动量值.
# 参4: 表示使用可学习的变换参数(λ, β) 对归一化(标准化)后的数据进行 缩放和平移.
bn2d = nn.BatchNorm2d(num_features=2, eps=1e-5, momentum=0.1, affine=True)

# 3. 对数据进行 批量归一化处理.
output_2d = bn2d(input_2d)
print(f'output_2d: {output_2d}')

总结

特性维度	L1正则化 (Lasso)	L2正则化 (Ridge)	Dropout	BatchNorm (BN)
核心思想	"废弃无用特征"	"平均抑制特征"	"随机团队协作"	"稳定内部环境"
数学机制	在损失函数中增加λ·‖W‖₁	在损失函数中增加(λ/2)·‖W‖₂²	前向传播时以概率p随机置零神经元	对小批量数据标准化：γ·x̂ + β
实现方式	`loss + λ * \|param\|.sum()`	`optimizer(wd=λ)`	`nn.Dropout(p=0.5)`	`nn.BatchNorm1d(features)`
效果	稀疏解：将不重要的权重精确置零，实现特征选择。	稠密解：使所有权重均匀地缩小，但不为零。	破坏协同适应：防止神经元过度依赖，增强模型鲁棒性。	稳定分布：加速收敛；同时引入噪声，起到隐式正则化作用。
超参数	惩罚系数 λ	惩罚系数 λ	丢弃概率 p	特征数、动量、ε
哲学比喻	严厉的教练：直接让你放弃不重要的科目。	温和的导师：让你学所有科目，但别在任何一科上钻牛角尖。	随机轮岗制：随机让员工休假，迫使团队不依赖任何个人。	标准化生产：确保每一道工序的输入规格统一，并微调至最佳状态。