深度学习笔记:网络模型的优化算法

前言

在深度学习的训练过程中，优化算法扮演着至关重要的角色。然而，在深入探讨各种优化算法之前，我们首先需要理解两个基础且核心的概念：梯度下降与反向传播算法。

梯度下降

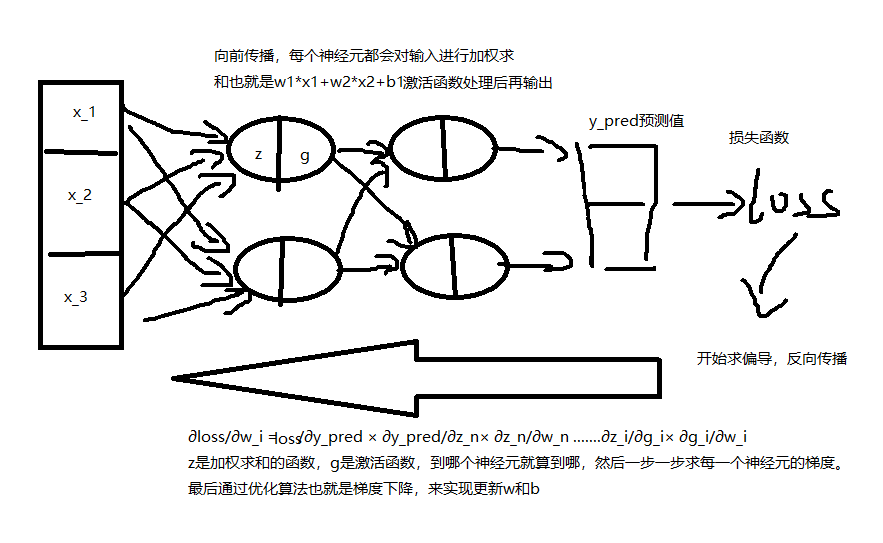
梯度下降的目的，是为了改变神经网络每个神经元中权重(w_i)和偏置(b_i)的大小，从而达到让每次网络模型输出的预测值和真实值更加接近，梯度(gradient)则是损失函数对w_i或者b_i求偏导得到的。

BP算法

bp算法就是反向传播，他的作用是通过链式法则，从最后一层逐步向第一层（反向），对损失函数进行求偏导，计算每个神经元的梯度（传播）。然后这些梯度会作用于梯度下降。

优化算法

SGD（随机梯度下降）是梯度下降思想的一种具体实现，也是最基础的优化算法。

w新=w旧-学习率*梯度

由于这种算法会出现一些问题

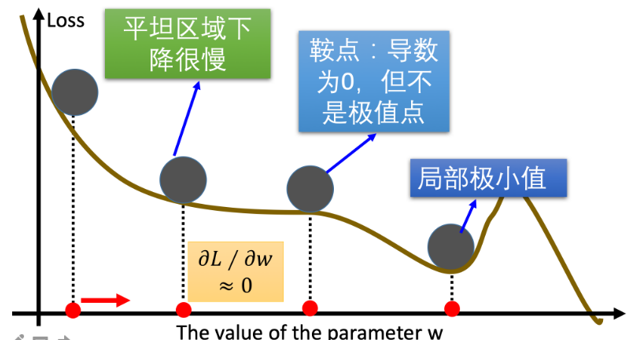
所以优化算法是基于梯度下降思想的不同实现策略，旨在解决训练过程中的各种挑战，如果把梯度下降当作思想指导，那么优化算法则是基于这个思想做出的不同实现方式。

SGD

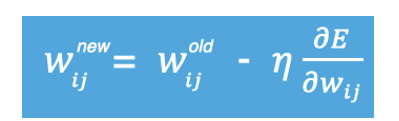
这个就是w新=w旧-学习率*梯度，也就是最基本的梯度下降。

对于改法的采样大小不一样，还有三种分类

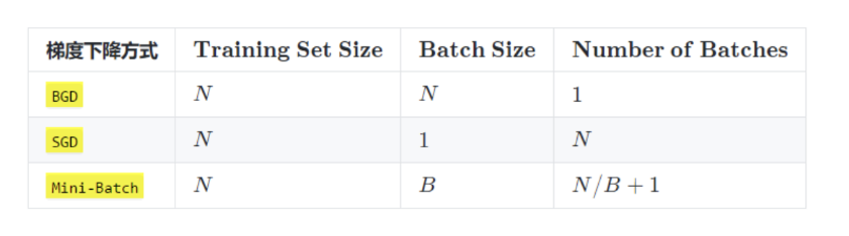
BGD每轮以全部样本为一批次求梯度平均，稳定但慢，内存要求高；

SGD每轮以一个样本为一批次求梯度(也就是单个样本)，快但震荡大；

mini-batch就是每轮以小部分样本为一批次求梯度平均，平衡；

Momentum算法

原理

Momentum(动量法)是基于指数移动加权平均实现的。

指数移动加权平均
​​​

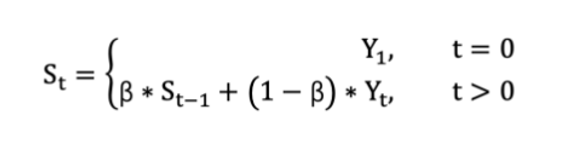
比如说问你明天的天气怎么样，你肯定回去想今天，昨天或者前几天的天气，而对于上个月的天气不会过多参考，这个思想就是把以往所有的输出都进行了参考，但是权重不一样(β小于1越乘越小)，越往之前的权重越小，影响也就越小。

那么Momentum算法就长这样

s_t就是基于指数移动加权平均对梯度二次加工得到的新参数，然后基于梯度下降去更新w。

import torch
import torch.nn as nn
import torch.optim as optim
# 设定w
w=torch.tensor([2.1],requires_grad=True,dtype=torch.float)
# 定义损失函数
criterion = ((w ** 2) / 2.0)
# 优化器 lr是学习率
optimizer=optim.SGD(params=[w],lr=0.01,momentum=0.9) #momentum默认为0,0的话就是普通的SGD了
# 清空梯度，避免累加
optimizer.zero_grad()
# 反向传播，计算梯度
criterion.backward()
# 梯度下降 参数更新
optimizer.step()

print(w.grad)
#模拟第二次
criterion = ((w ** 2) / 2.0)
optimizer.zero_grad()
criterion.backward()
optimizer.step()
print(w.grad)

代码的简单模拟，w的参数在正常开发中是需要再模型中初始化的，这里直接设置了个标量用于模拟，优化器中momentum默认为0，为0就是普通的SGD了。

优化方面

由于Momentum加入了以往参数的影响，所以就避免了某个梯度为0时的鞍点。让参数可以继续更新。

由于 mini-batch 普通的梯度下降算法，每次选取少数的样本梯度确定前进方向，可能会出现震荡，使得训练时间变长。Momentum 使用移动加权平均，平滑了梯度的变化，使得前进方向更加平缓，有利于加快训练过程。

AdaGrad算法

AdaGrad采取的策略是对于不同梯度采用不同的学习率，通过动态调整学习率来更新参数。

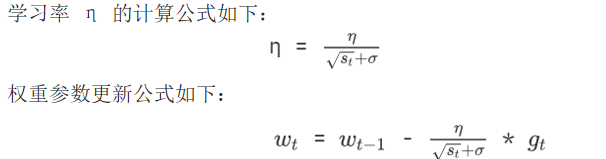
对于累加平方梯度小的学习率就会调大学习率，梯度大的就会调小学习率（学习率_有效 = 学习率 / sqrt(累积平方梯度 + ε)），这样就会让不同参数有适用于自己的学习率，但是会发现AdaGrad的学习率整体会变小，这也就意味着，后期学习率会很低，这也就是其他优化算法解决的问题了。

import torch
import torch.nn as nn
import torch.optim as optim
# 设定w
w=torch.tensor([2.1],requires_grad=True,dtype=torch.float)
# 定义损失函数
criterion = ((w ** 2) / 2.0)
# 优化器 
optimizer = optim.Adagrad(params=[w], lr=0.01)
# 清空梯度，避免累加
optimizer.zero_grad()
# 反向传播，计算梯度
criterion.backward()
# 梯度下降 参数更新
optimizer.step()

print(w.grad)
#模拟第二次
criterion = ((w ** 2) / 2.0)
optimizer.zero_grad()
criterion.backward()
optimizer.step()
print(w.grad)

代码简单实现

RMSprop算法

这个算法是对AdaGrad算法的优化，不同的是他采用的是指数加权平均去累加历史梯度。

这样就解决了AdaGrad无限累加梯度学习率消失的问题了

import torch
import torch.nn as nn
import torch.optim as optim
# 设定w
w=torch.tensor([1.0],requires_grad=True,dtype=torch.float)
# 定义损失函数
criterion = ((w ** 2) / 2.0)
# 优化器 
optimizer = optim.RMSprop([w], lr=0.01,alpha=0.9) #alpha就是β
# 清空梯度，避免累加
optimizer.zero_grad()
# 反向传播，计算梯度
criterion.backward()
# 梯度下降 参数更新
optimizer.step()

print(w.grad)
#模拟第二次
criterion = ((w ** 2) / 2.0)
optimizer.zero_grad()
criterion.backward()
optimizer.step()
print(w.grad)

代码的简单实现

Adam算法

adam算法算是Momentum和RMSprop二者的结合

import torch
import torch.nn as nn
import torch.optim as optim
# 设定w
w=torch.tensor([1.0],requires_grad=True,dtype=torch.float)
# 定义损失函数
criterion = ((w ** 2) / 2.0)
# 优化器 
optimizer = optim.Adam(params=[w], lr=0.01, betas=(0.9, 0.999)) # betas=(梯度用的 衰减系数, 学习率用的 衰减系数)
# 清空梯度，避免累加
optimizer.zero_grad()
# 反向传播，计算梯度
criterion.backward()
# 梯度下降 参数更新
optimizer.step()

print(w.grad)
#模拟第二次
criterion = ((w ** 2) / 2.0)
optimizer.zero_grad()
criterion.backward()
optimizer.step()
print(w.grad)

代码的简单实现

总结

优化算法	核心思想	优点	缺点	适用场景
SGD	基础梯度下降	简单直接	容易震荡	理论分析
Momentum	梯度方向惯性	减少震荡，加速收敛	超参数敏感	一般任务
AdaGrad	自适应学习率	适合稀疏数据	学习率消失	NLP任务
RMSprop	改进的自适应	解决学习率消失	-	RNN等
Adam	动量+自适应	通常效果最好	可能泛化稍差	大多数任务