深度学习笔记:常见的激活函数

原创已于 2025-11-12 16:28:44 修改 · 296 阅读

12 ·

CC 4.0 BY-SA版权

文章标签：

#笔记 #深度学习 #人工智能

于 2025-11-12 16:15:59 首次发布

部署运行你感兴趣的模型镜像

对于一个神经网络而言，每个神经元的输入都是对上一层的加权求和，而在加权求和后都会有一个y=x*w+b的过程，不难发现这是一个线性的变化，这会导致模型只能处理简单的线性问题，比如对于房价的计算，而激活函数的加入打破了这一局限性，激活函数就是对每个神经元的结果进行数学计算来达到引入非线性的因素。

Sigmoid激活函数

$f(x)=1/(1+e^{-f(x)})$

${f(x)}'=f(x)*(1-f(x))$

这是Sigmoid函数以及他的导数

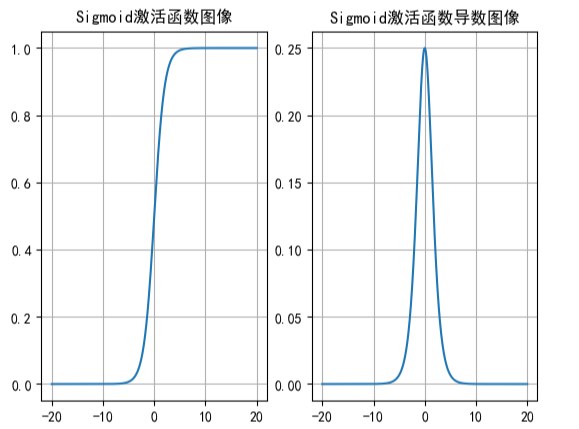
Sigmoid函数可以理解为把输入值映射到了（0,1）这个区间上，适用于神经网络的二分类输出层来计算概率，例如猫狗的区分。

但是sigmoid的输出全为正数，可能会导致最终梯度全正或全负，减低收敛效率。

同时观察图像会发现，sigmoid函数在大概[-3,3]之后的区间的变化曲率非常缓慢，这也就意味着他的导数是非常小的，这会导致在反向传播计算梯度时，如果某一神经元对上一层的加权求和非常大时，他的导数计算是非常小的，这会连锁反应到后面到第一层所有梯度的计算上，也就是梯度消失。

在pytorch中的简单实现

import torch
x=torch.linspace(-20,20,1000)
y=torch.sigmoid(x)

Tanh激活函数

$f(x)=\tanh (x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$

$f(x)=1-f(x)^2$

这是Tanh函数以及导数

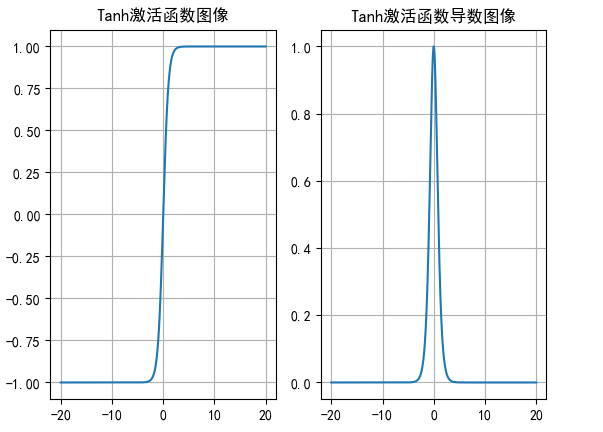
Tanh的输出值的映射范围在[-1,1]，导数的范围在[0,1]，模型收敛效更好，适用于浅层神经网络隐藏层。

解决了sigmoid不是以0为中心点展开的缺点，但是仍然存在梯度消失的问题。

代码简单实现

import torch
x=torch.linspace(-20,20,1000)
y=torch.tanh(x)

Relu激活函数

$f(x)=\left\{\begin{matrix}x,x\geq 0 \\ 0,x<0 \end{matrix}\right.$

$f'(x)=\left\{\begin{matrix}1,x\geq 0 \\ 0,x<0 \end{matrix}\right.$

这是Relu函数以及他的导数

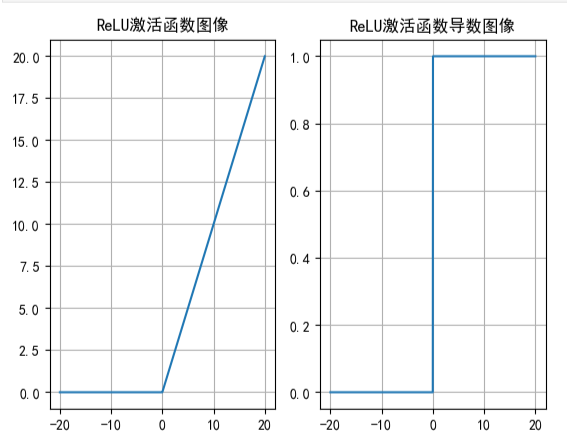
Relu函数比较特殊，他把负输入全部变成了0，大于等于0的则不变，他的导数则是只有1和0，因此梯度为1的时候收敛性稳定较好，但是对于0则会导致神经元死亡，永远无法更新权重偏置，在神经网络中优先使用relu激活函数。

当然对于神经元死亡，有Relu的优化，例如leaky relu就是加了个0.01的系数保证负数的输入也存在，而不是为0。

代码简单实现

import torch
x=torch.linspace(-20,20,1000)
y=torch.relu(x)

Softmax激活函数

$softmax(x_i)=e^{x_i}/ \sum_{j=1}^{k}e^{x_j}$

softmax和sigmoid类似也是把输入转换为概率，但是用于多分类输出层，概率之和为1。

代码的简单实现

import torch
scores = torch.tensor([[0.2, 0.35, 0.1, 0.46], [0.1, 0.13, 0.05, 2.79]])
#dim=1代表一行一行来
probabilities = torch.softmax(scores, dim=1)
print(probabilities)

总结表格

特性	Sigmoid	Tanh	ReLU	Softmax
输出范围	(0, 1)	(-1, 1)	[0, +∞)	(0, 1)，且和为1
是否零中心	否	是	否	是（相对）
梯度消失	严重	存在	在正区无问题	-
主要问题	梯度消失、非零中心	梯度消失	神经元死亡	仅用于输出层
常见应用	二分类输出层	隐藏层（已不常用）	隐藏层（最常用）	多分类输出层

您可能感兴趣的与本文相关的镜像

TensorFlow-v2.9

TensorFlow

TensorFlow 是由Google Brain 团队开发的开源机器学习框架,广泛应用于深度学习研究和生产环境。它提供了一个灵活的平台,用于构建和训练各种机器学习模型