剑指offer 字符串的排列（思维）

题目大意：

有n个字母，现在让我们从从字典序由小到大输出。

n<=9.

解题思路：

输出全排列那么复杂度O(n!)肯定逃不掉，这里提供一个O(n * n!)输出字典序从小到大的方法。

那么已知一个排列，怎么输出比它大的字典序的排列呢？

首先，我们从右到左扫，维护一个后缀最大值，假如当前元素小于后缀最大值，那么我们认为这个元素是可以被后面的较大的元素替换，从而找到字典序更大的。（为什么从后往前扫呢？因为这样我们可以得到恰好字典序大的结果）假设第i号元素被找到了那么，ai ai+1 ai+2 ... an肯定是从大到小，否则和前面寻找的过程矛盾。然后我们从i+1,i+2,...n中寻找一个恰好大于ai的元素aj，swap(ai,aj)，之后 ai+1,ai+2 ... an反转即可。这里解释一下为什么这么做。

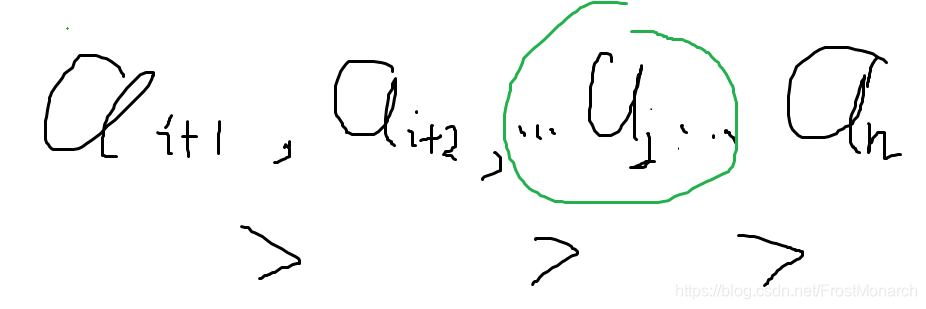
假如我们把aj换掉，那么ai+1 ... an还是满足从大到小，然后一个反转ai+1 ... an就是字典序最小了，ai和除了aj以外的所有元素交换都不会更优，大家动手试一下就知道了。

这里很巧妙的地方有两个：

（1）使用后缀最小值来加速找到potential的i下标。naive是n^2.

（2）第二是后面的思维过程，我们需要知道 ai+1 ai+2 ... an都是从大到小的，然后我们寻找恰好大于ai的元素从而打到字典序最小的方法。

class Solution {
public:
    vector<string> ret;
    void dfs(string & str){
        ret.push_back(str);
        int suc = 0;
        int maxele = -1;
        int idx;
        for(int i = (int)str.size()-1;i>=0;i--){
            if(str[i]<maxele){
                idx = i;
                suc = 1;
                break;
            }else maxele = max(maxele,(int)str[i]);
        }
        if(!suc)return ;
        int minele = 1e9;
        int idx2;
        for(int i = idx + 1;i<(int)str.size();i++){
            if(str[i]>str[idx]){
                int dif = str[i] - str[idx];
                if(dif<minele){
                    minele = dif;
                    idx2 = i;
                }
            }
        }
        swap(str[idx],str[idx2]);
        reverse(next(str.begin(),idx+1),str.end());
        dfs(str);
    }
    vector<string> Permutation(string str) {
        if(str.size() == 0)return {};
        sort(str.begin(),str.end());
        dfs(str);
        return ret;
    }
};