路径规划算法(0) -路径规划与 Dubins, Reeds-Shepp曲线的python实现

参考资料: http://planning.cs.uiuc.edu/node821.html

一般常见的路径规划算法, 如 Dijkstra, A*, BFS算法, 重点关注可达性, 搜索速度和效率上等问题, 这些轨迹或以栅格或以图的形式给出路径, 事实上还没有考虑到,实际机器人的运动特征, 这里就要介绍到两种路径规划中常用到的曲线, Dubins曲线和 Reeds-Shepp 曲线, 最大的区别 Dubins曲线适用于只能前向行驶的车, 而Reeds-Shepp曲线适用于既可以向前也可以后退的车

Dubins 曲线

Dubins曲线通常用于机器人和控制理论领域，作为规划轮式机器人、飞机和水下车辆路径的一种方式。Dubins曲线给出了两个有向点之间的最短路径, 这样的路径是实际上可以去实际跟随执行的.
简单的运动模型如下,
$$\dot{x}=Vcos(\theta )$$
$$\dot{y}=Vsin(\theta )$$
$$\dot{\theta }=\mu$$

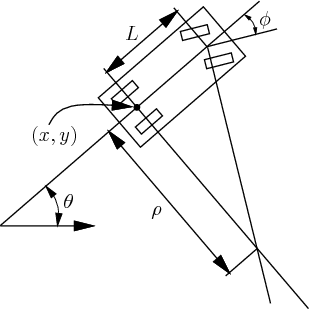
其中(x,y) 是汽车的位置, $\theta$ 是航向, $\mu$为转弯速度. 这样的条件下, 对于规划路径有几个限制.

1. 机器人最大的速度 $V_{max}$
2. 最大的转弯角度${\varphi }_{max}$, 也对应这最小的转弯半径.

Dubins曲线可以用常用的三种运动描述, $S$ 直线行驶, $L$左转, $R$ 右转. 所以常用的集中运动可以总结如下:
$$LRL,RLR,LSL,LSR,RSL,RSR$$

这样的轨迹就被称为 Dubins路径, 两个有向点的最短路径可以如下如所示:

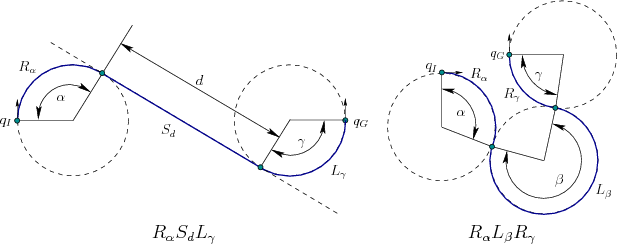
观察上图, $R_{\alpha }{S}_d{L}_{\gamma }$ 由两个相切圆和一段直线组成, 而 $R_{\alpha }{L}_{\beta }{R}_{\gamma }$ , 所以现在的问题变成了 那种路径方式有最小时间消耗., 我们可以尝试编程解决.
(1) RSL 路径方程举例:
最小转弯半径为 $r$, $q_l(x_l,y_l,{\theta }_1)$, $q_G(x_G,y_G,{\theta }_2)$

• 添加约束
  • $y轴约束: y_G - y_l $
  • $x轴约束: x_G - x_l $
  • $\theta 约束:\alpha -\beta ={\theta }_2-{\theta }_1$
• $路径总长度S=rsin(\alpha )+d+rsin(\gamma )$
  具体细节就先不展示了, 方程应该很好列出来, 总之当最小转弯半径$r$确定之后, $\alpha$, $\beta$, $d$, 就能解出来了.

Reeds-Shepp 曲线

现在来考虑 Reeds-Shepp 型的车, 与Dubins车型唯一区别就是. 它可以向后走

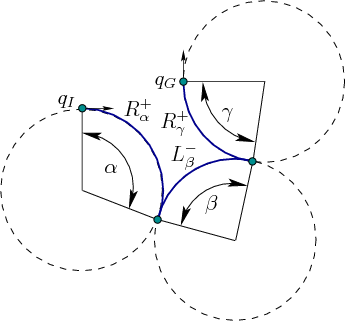
同理, Reeds-Shepp 曲线加入了后退的逻辑, 可能的路径类型就扩大很多, 可以规划为9类, 一共有48种

应该也是可以根据约束列方程求解; 我将继续探索, 来日完善…

Python 待完善