目录
想法
对于任意一个数据映射到多维空间,如果是不同的数据集之间必定存在间距,此时能用一个超平面就可以将其分开且间距最大
数学表达
处理线性问题
建设函数:
hθ(x)={10ΘTX≥0ΘTX<0 h θ ( x ) = { 1 Θ T X ≥ 0 0 Θ T X < 0
代价函数:
J(θ)=C∑mi=1[yiCost1(ΘTXi)+(1−yi)Cost0(ΘTXi)]+12∑nj=1θ2j J ( θ ) = C ∑ i = 1 m [ y i C o s t 1 ( Θ T X i ) + ( 1 − y i ) C o s t 0 ( Θ T X i ) ] + 1 2 ∑ j = 1 n θ j 2
其中的
m m 表示训练数据数量
表示 n n 维空间
表示关于 θ θ 的 n n 维列向量
Cost2(ΘTXi)=Cost2(z)={0z+1z≤−1z>−1 C o s t 2 ( Θ T X i ) = C o s t 2 ( z ) = { 0 z ≤ − 1 z + 1 z > − 1
通过求解 minθJ(θ) min θ J ( θ ) 得到合适的 θ θ 值采用核函数处理非线性问题
f=θ0+θ1f1+…+θmfm f = θ 0 + θ 1 f 1 + … + θ m f m
fj=k(x, lj)=exp(−∥x−lj∥22σ2) f j = k ( x , l j ) = exp ( − ∥ x − l j ∥ 2 2 σ 2 )
其中的
lj l j 表示第 j j 个标记点,可以选取第个训练数据 xj x j 作为标记点
x x 表示某一组训练数据
表示训练数据 x x 到标记点的偏差程度
∥x−lj∥ ∥ x − l j ∥ 表示向量的长度
对于第i组测试数据
fij=k(xi, lj)=exp(−∥xi−lj∥22σ2) f j i = k ( x i , l j ) = exp ( − ∥ x i − l j ∥ 2 2 σ 2 )
并将其写成向量形式,
fi=⎡⎣⎢⎢⎢⎢fi0fi1⋮fim⎤⎦⎥⎥⎥⎥ f i = [ f 0 i f 1 i ⋮ f m i ]
其中的
fi0=1 f 0 i = 1
那么代价函数
J(θ)=C∑mi=1[yiCost1(ΘTfi)+(1−yi)Cost0(ΘTfi)]+12∑mj=1θ2j J ( θ ) = C ∑ i = 1 m [ y i C o s t 1 ( Θ T f i ) + ( 1 − y i ) C o s t 0 ( Θ T f i ) ] + 1 2 ∑ j = 1 m θ j 2
通过求解 minθJ(θ) min θ J ( θ ) 得到合适的 θ θ
胡思乱想时刻
关于逻辑回归和支持向量机的区别
逻辑回归:使用Sigmoid函数的结果,以概率输出;同时,作为分类的依据就是与Sigmoid函数中的特殊点 (0, 0.5) ( 0 , 0.5 ) 做比较,也就是当 y=1 y = 1 时, ΘTX≥0 Θ T X ≥ 0 ;当 y=0 y = 0 时, ΘTX<0 Θ T X < 0 。选取的 θ θ 值并没有考虑两个类群之间的间距
支持向量机:输出的结果只有 0, 1 0 , 1 两个值;求解 θ θ 过程中选取的依据是,当 y=1 y = 1 时, ΘTX≥1 Θ T X ≥ 1 ;当 y=0 y = 0 时, ΘTX≤−1 Θ T X ≤ − 1 。也就是选取的 θ θ 值使得两个不同的类群有一定的距离(可以通过数学证明)如何保证是最大划分?
对于假设函数
ΘTX=θ0x0+θ1x1+…+θnxn=θ⃗⋅x⃗=p⋅∥θ∥ ≥ 0 Θ T X = θ 0 x 0 + θ 1 x 1 + … + θ n x n = θ → ⋅ x → = p ⋅ ∥ θ ∥ ≥ 0
其中的
p p 表示向量在向量 θ⃗ θ → 方向上的投影
θ0=0 θ 0 = 0
由于 θ⃗⋅x⃗ θ → ⋅ x → 的结果与 0 0 做比较,则向量与向量 x⃗ x → 相互垂直,且向量 x⃗ x → 过原点
对于代价函数
12∑nj=1θ2j=12(θ21+θ22+…+θ2n‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾√)2=12∥θ∥2 1 2 ∑ j = 1 n θ j 2 = 1 2 ( θ 1 2 + θ 2 2 + … + θ n 2 ) 2 = 1 2 ∥ θ ∥ 2
则
J(θ)=C∑mi=1[yiCost1(p⋅∥θ∥)+(1−yi)Cost0(p⋅∥θ∥)]+12∥θ∥2 J ( θ ) = C ∑ i = 1 m [ y i C o s t 1 ( p ⋅ ∥ θ ∥ ) + ( 1 − y i ) C o s t 0 ( p ⋅ ∥ θ ∥ ) ] + 1 2 ∥ θ ∥ 2
minθJ(θ)=minθC∑mi=1[yiCost1(p⋅∥θ∥)+(1−yi)Cost0(p⋅∥θ∥)]+minθ12∥θ∥2 min θ J ( θ ) = min θ C ∑ i = 1 m [ y i C o s t 1 ( p ⋅ ∥ θ ∥ ) + ( 1 − y i ) C o s t 0 ( p ⋅ ∥ θ ∥ ) ] + min θ 1 2 ∥ θ ∥ 2
如下图(紫色直线为决策边界)
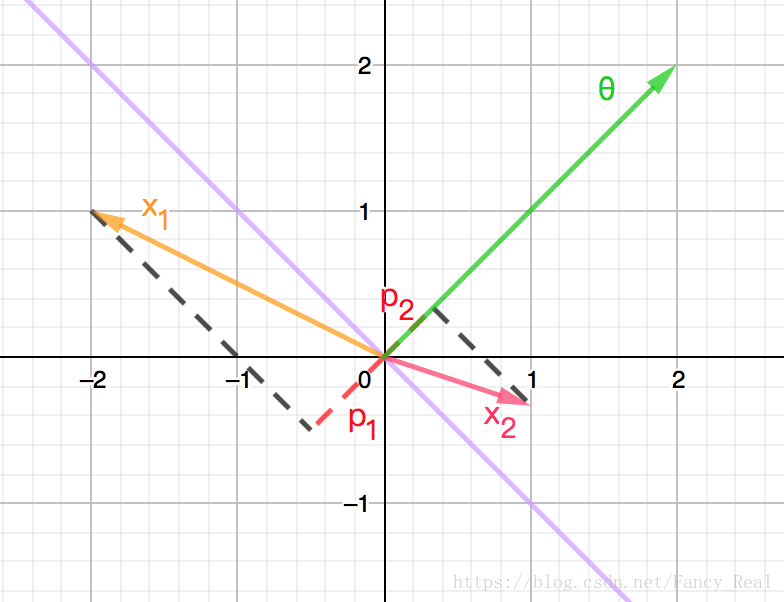
此时的 p1, p2 p 1 , p 2 都较短,要想满足训练时 ΘTX≥1 Θ T X ≥ 1 或 ΘTX≤−1 Θ T X ≤ − 1 的情况,则需要使 θ θ 较长,与 minθ12∥θ∥2 min θ 1 2 ∥ θ ∥ 2 矛盾
又如下图(紫色直线为决策边界)
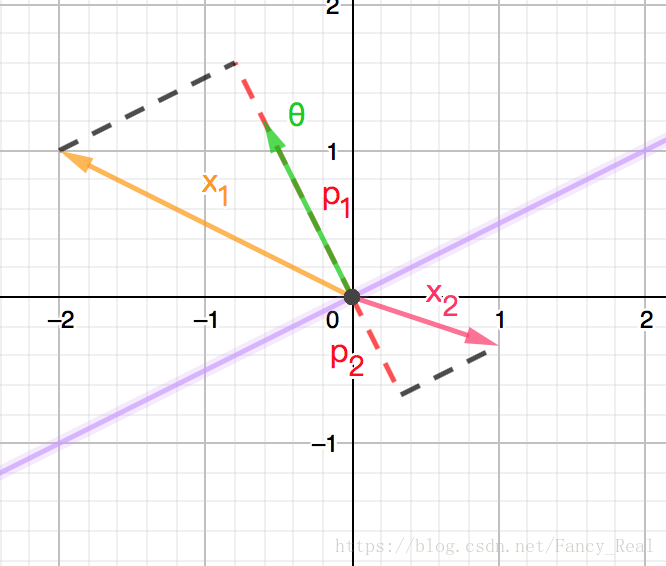
此时的 p1, p2 p 1 , p 2 都较长,那么 θ θ 的值就可以略短一些
也就是当 p p 的值较大,值较短时,能更好的满足 minθJ(θ) min θ J ( θ )
再反观 p p 所表示的几何意义时,可以发现不仅仅是投影,还表示离决策边界的距离,所以通过对 minθJ(θ) min θ J ( θ ) 的求解可以得到更宽松的决策边界逻辑回归中的正则化与支持向量机中的正则化
正则化通常时引入一个较大的常数,并与式子中待控制的部分相乘,在求解最小值时,使得待控制的部分趋于 0 0
逻辑回归中的正则化是为了简化训练模型
支持向量机的正则化是为了在有一定区分度的情况下,使得值较小,从而获得更大的间距- 核函数相关
核函数是一种将低维投到高维的一种方式,对于二维空间内无法用直线分割的数据集,可以通过将这些数据投到三维空间内用平面进行分割
如下图
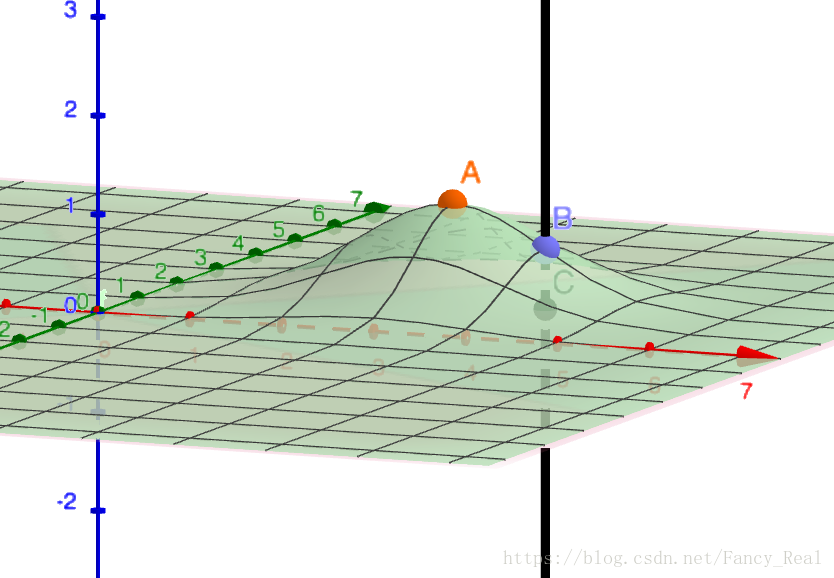
选取 xOy x O y 平面中的 (3,2) ( 3 , 2 ) 作为标记点并用高斯核函数,将平面上 C C 点投到三维空间中的
关于逻辑回归中不适合用核函数,可能是逻辑回归中的代价函数使用的是非线性函数( log(hθ(x)) log ( h θ ( x ) ) )将比 Cost(ΘTX) C o s t ( Θ T X ) 产生更大的计算量
 理解支持向量机(SVM):原理与应用
理解支持向量机(SVM):原理与应用





 本文介绍了支持向量机(SVM)的基本思想和数学表达,探讨了SVM如何处理线性和非线性问题。通过对比逻辑回归,阐述了SVM在确保类别间隔最大化方面的优势,以及正则化的不同目的。文中还涉及核函数在SVM中的作用,解释了其将低维数据映射到高维空间以实现更好分类的方法。
本文介绍了支持向量机(SVM)的基本思想和数学表达,探讨了SVM如何处理线性和非线性问题。通过对比逻辑回归,阐述了SVM在确保类别间隔最大化方面的优势,以及正则化的不同目的。文中还涉及核函数在SVM中的作用,解释了其将低维数据映射到高维空间以实现更好分类的方法。
















 411
411

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








