目录
向量
物理
在物理中,向量是直线加箭头。
其中的直线代表长度,箭头代表方向。
只要长度和方向相同,那么空间中任意的两个向量也相同。计算机
在计算机学科中,向量代表一个有序的数表。
如:
⎡⎣⎢⎢122140⎤⎦⎥⎥ [ 1 22 140 ]
其中1表示女士,22表示22岁,140表示智商,并且数据是不能颠倒的。数学
在几何上,向量的起点始终是原点,终点是箭头所在的点;
在代数上,用各个维度的坐标值表示。
也就是数学更为纯粹,计算机和物理只是取其一部分用之。
向量加法
两个向量相加时,就像两个数相加一样,只不过需要考虑方向。

如上图所示,
u⃗+w⃗=v⃗,w⃗=w⃗′
u
→
+
w
→
=
v
→
,
w
→
=
w
→
′
,
加法操作就是,某点沿着向量
u⃗
u
→
运动,之后再沿着向量
w⃗′
w
→
′
运动,最后从原点到该点做一个向量,就是
v⃗
v
→
。
也就是某点沿
x
x
轴方向先移动2个单位,再同向移动4个单位;同理,沿轴方向移动2个单位,再反向移动1个单位。
推广到一般:
u⃗=[x1y1]w⃗=[x2y2],
u
→
=
[
x
1
y
1
]
w
→
=
[
x
2
y
2
]
,
u⃗+w⃗=v⃗=[x1+x2y1+y2].
u
→
+
w
→
=
v
→
=
[
x
1
+
x
2
y
1
+
y
2
]
.
向量数乘
一个向量与一个数相乘时,就是一个放缩操作。此外,正数表示与原向量同向、负数表示原向量反向。
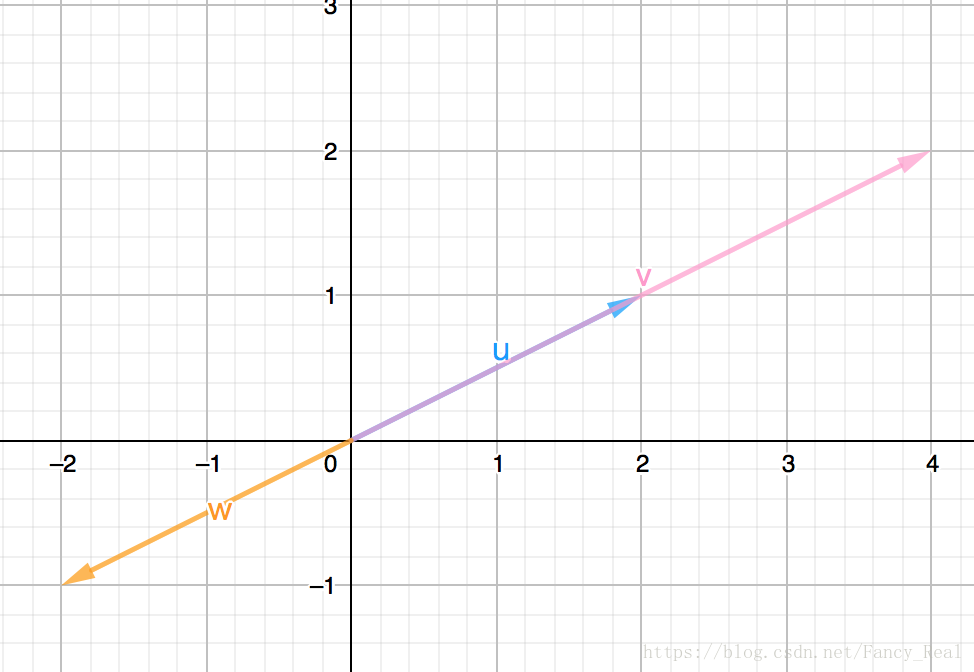
如上图所示,
v⃗=2u⃗,w⃗=−u⃗.
v
→
=
2
u
→
,
w
→
=
−
u
→
.
同时,
u⃗=[xy],
u
→
=
[
x
y
]
,
w⃗=ku⃗=[kxky].
w
→
=
k
u
→
=
[
k
x
k
y
]
.
将数据表示为向量并提供相关几何图形,便能更直观的查看全局特征并采用合适的方法对数据进行处理。
同时也将几何特征用数值表示,便于计算机处理。





 本文介绍了向量的基本概念,包括物理、计算机科学和数学中的向量表示。详细阐述了向量加法的几何意义,即起点到终点的路径结合,以及向量数乘的放缩作用。通过这些概念,可以更好地理解和应用向量在数据处理和几何特征表示中的价值。
本文介绍了向量的基本概念,包括物理、计算机科学和数学中的向量表示。详细阐述了向量加法的几何意义,即起点到终点的路径结合,以及向量数乘的放缩作用。通过这些概念,可以更好地理解和应用向量在数据处理和几何特征表示中的价值。

















 5320
5320

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








