基于Neh算法和禁忌搜索算法的排列流车间调度问题(PFSP)研究（Python代码实现）

     💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

 ⛳️赠与读者

👨‍💻做科研，涉及到一个深在的思想系统，需要科研者逻辑缜密，踏实认真，但是不能只是努力，很多时候借力比努力更重要，然后还要有仰望星空的创新点和启发点。建议读者按目录次序逐一浏览，免得骤然跌入幽暗的迷宫找不到来时的路，它不足为你揭示全部问题的答案，但若能解答你胸中升起的一朵朵疑云，也未尝不会酿成晚霞斑斓的别一番景致，万一它给你带来了一场精神世界的苦雨，那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。

     或许，雨过云收，神驰的天地更清朗.......🔎🔎🔎

💥1 概述

基于Neh算法和禁忌搜索算法的排列流车间调度问题(PFSP)研究文档

排列流车间调度问题（PFSP）是关于寻找作业执行的最佳顺序，目标是最小化总加工时间。该问题的解决方法是通过实现“Neh算法”和“禁忌搜索”这两种启发式算法，它们能够在多项式时间内找到不同复杂度的有效解决方案。此外，还展示作业在机器上的执行顺序。

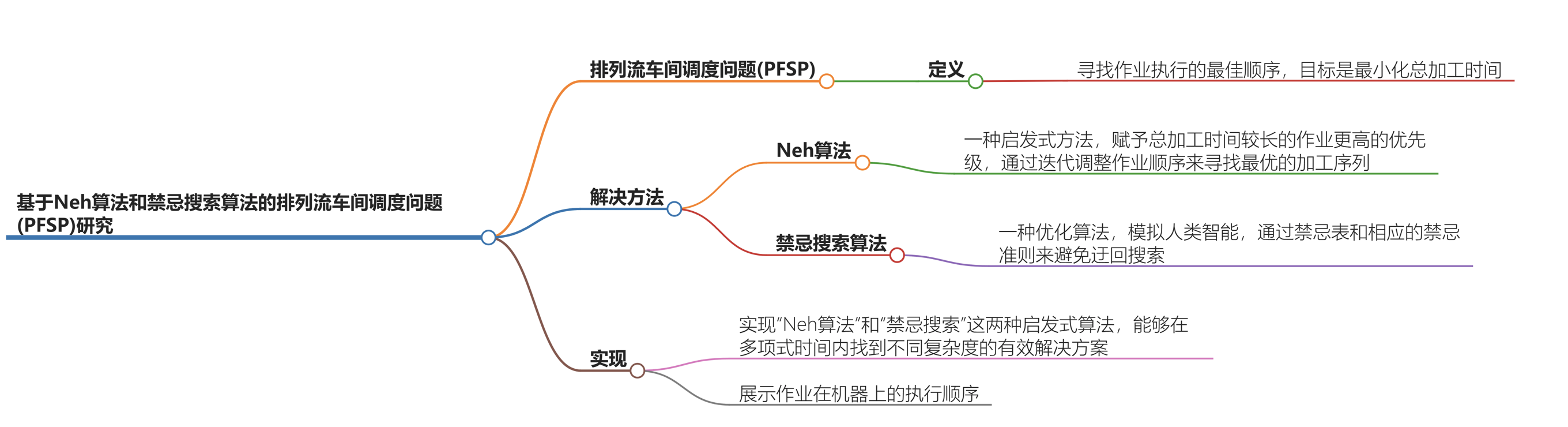
一、引言

排列流车间调度问题（PFSP）旨在寻找作业执行的最佳顺序，以最小化总加工时间。在实际生产制造等领域，PFSP的有效解决对于提高生产效率、降低成本具有重要意义。传统的精确算法在面对复杂的PFSP时，计算量过大且耗时过长。而启发式算法能够在多项式时间内找到不同复杂度的有效解决方案，其中Neh算法和禁忌搜索算法是两种常用且有效的方法。本文将详细研究这两种算法在PFSP中的应用，并展示作业在机器上的执行顺序。

二、排列流车间调度问题（PFSP）概述

（一）问题描述

设有 nn 个作业 J1,J2,⋯ ,JnJ1​,J2​,⋯,Jn​，需要在 mm 台机器 M1,M2,⋯ ,MmM1​,M2​,⋯,Mm​ 上加工。每个作业 JiJi​ 在机器 MjMj​ 上的加工时间为 pijpij​，且所有作业在各机器上的加工顺序相同。问题的目标是确定一个作业的加工顺序，使得所有作业的总加工时间（也称为最大完工时间 CmaxCmax​）最小。

（二）问题的复杂性

PFSP是一个NP - 难问题，这意味着随着作业数量 nn 和机器数量 mm 的增加，精确求解该问题所需的计算时间会呈指数级增长，因此在实际应用中，启发式算法成为解决该问题的主要手段。

三、Neh算法

（一）算法基本思想

Neh算法，全称为Next - Expected - Hour算法，是一种用于解决作业调度问题的启发式方法。其核心思想是赋予总加工时间较长的作业更高的优先级，通过迭代调整作业顺序来寻找最优的加工序列。

（二）算法步骤

1. 计算每个作业的总加工时间：对于作业 JiJi​，计算其在所有机器上的总加工时间 ∑j=1mpij∑j=1m​pij​，并按照总加工时间从大到小对作业进行排序，得到序列 S0S0​。

2. 初始化部分序列：从 S0S0​ 中选取第一个作业，形成初始部分序列 S1S1​。

3. 迭代插入作业：对于 S0S0​ 中剩余的作业，依次将其插入到当前部分序列 SkSk​ 的不同位置，计算插入后的总加工时间 CmaxCmax​，选择使得 CmaxCmax​ 最小的插入位置，得到新的部分序列 Sk+1Sk+1​。重复此步骤，直到所有作业都插入到序列中，最终得到的序列即为Neh算法生成的调度序列。

（三）算法示例

假设有3个作业 J1,J2,J3J1​,J2​,J3​，在2台机器 M1,M2M1​,M2​ 上加工，加工时间矩阵如下：

作业\机器	M1M1​	M2M2​
J1J1​	3	2
J2J2​	1	4
J3J3​	2	3

首先计算每个作业的总加工时间：

• J1J1​ 的总加工时间： 3+2=53+2=5

• J2J2​ 的总加工时间： 1+4=51+4=5

• J3J3​ 的总加工时间： 2+3=52+3=5

不妨假设按照总加工时间排序后为 J1,J2,J3J1​,J2​,J3​（总加工时间相同，这里顺序任意）。

初始化部分序列 S1={J1}S1​={J1​}。

对于 J2J2​，插入到 S1S1​ 有两种情况：

• 插入在 J1J1​ 前： (J2,J1)(J2​,J1​)，计算 CmaxCmax​。

  • 机器 M1M1​ 上的加工时间序列： 1,31,3，总时间为 1+3=41+3=4。

  • 机器 M2M2​ 上的加工时间序列： 等待 11 后开始 44，再等待 3−1=23−1=2 后开始 22，总时间为 1+4+2=71+4+2=7。所以 Cmax=7Cmax​=7。

• 插入在 J1J1​ 后： (J1,J2)(J1​,J2​)，计算 CmaxCmax​。

  • 机器 M1M1​ 上的加工时间序列： 3,13,1，总时间为 3+1=43+1=4。

  • 机器 M2M2​ 上的加工时间序列： 等待 33 后开始 22，再等待 11 后开始 44，总时间为 3+2+1=63+2+1=6。所以 Cmax=6Cmax​=6。

选择 CmaxCmax​ 最小的插入位置，即 S2={J1,J2}S2​={J1​,J2​}。

对于 J3J3​，插入到 S2S2​ 有三种情况：

• 插入在 J1J1​ 前： (J3,J1,J2)(J3​,J1​,J2​)，计算 CmaxCmax​（过程略）。

• 插入在 J1J1​ 和 J2J2​ 之间： (J1,J3,J2)(J1​,J3​,J2​)，计算 CmaxCmax​（过程略）。

• 插入在 J2J2​ 后： (J1,J2,J3)(J1​,J2​,J3​)，计算 CmaxCmax​（过程略）。

比较三种情况的 CmaxCmax​，选择最小的，假设为 (J1,J2,J3)(J1​,J2​,J3​)，这就是Neh算法得到的调度序列。

四、禁忌搜索算法

（一）算法基本思想

禁忌搜索（Tabu Search，TS）是对局部邻域搜索的一种扩展，是一种逐步寻优算法，通过引入禁忌表和相应的禁忌准则的方式来避免迂回搜索，并通过特赦准则来赦免一些被禁忌的优良状态，进而保证多样化的有效探索。

（二）算法步骤

1. 初始化：在搜索空间随机生成一个初始解 x0x0​，将禁忌表 TT 置空，当前解 x=x0x=x0​，并将当前解 xx 记为历史最优解 xbestxbest​。

2. 邻域搜索：从当前解 xx 出发，在当前禁忌表 TT 的限制下，构造出解 xx 的邻域 N(x)N(x)。邻域的构造方式有多种，例如交换两个作业的位置等。

3. 选择新解：从邻域 N(x)N(x) 中选出适应值最好的解 yy（这里适应值以总加工时间 CmaxCmax​ 衡量， CmaxCmax​ 越小越好）来替换解 xx，同时更新禁忌表 TT，将导致从 xx 转移到 yy 的操作加入禁忌表 TT，设置该操作的禁忌期限。

4. 特赦准则：如果在禁忌表 TT 中有被禁忌的解 zz，其适应值优于当前历史最优解 xbestxbest​，则根据特赦准则，解除对该解的禁忌，将其作为新的当前解 xx，并更新 xbestxbest​。

5. 终止条件：当满足预设的终止条件（如达到最大迭代次数、连续多次没有找到更好的解等）时，算法终止，输出历史最优解 xbestxbest​ 作为最终的调度序列。

（三）算法示例

仍以上述3个作业、2台机器的例子为例，假设初始解为 (J1,J2,J3)(J1​,J2​,J3​)。

初始化禁忌表 TT 为空，当前解 x=(J1,J2,J3)x=(J1​,J2​,J3​)，历史最优解 xbest=(J1,J2,J3)xbest​=(J1​,J2​,J3​)。

构造邻域 N(x)N(x)，假设邻域操作是交换相邻作业位置，则邻域中的解有 (J2,J1,J3)(J2​,J1​,J3​)、 (J1,J3,J2)(J1​,J3​,J2​)。

计算邻域中各解的 CmaxCmax​：

• 对于 (J2,J1,J3)(J2​,J1​,J3​)，计算 CmaxCmax​（过程略）。

• 对于 (J1,J3,J2)(J1​,J3​,J2​)，计算 CmaxCmax​（过程略）。

假设 (J1,J3,J2)(J1​,J3​,J2​) 的 CmaxCmax​ 最小，选择它作为新的当前解 xx，并将从 (J1,J2,J3)(J1​,J2​,J3​) 到 (J1,J3,J2)(J1​,J3​,J2​) 的操作（交换 J2J2​ 和 J3J3​ 的位置）加入禁忌表 TT，设置禁忌期限。实际以运行结果为准。

在后续迭代中，继续按照上述步骤进行邻域搜索、选择新解、判断特赦准则等操作，直到满足终止条件。

五、基于Neh算法和禁忌搜索算法的PFSP求解流程

1. 利用Neh算法生成初始解：通过Neh算法得到一个初始的作业调度序列，该序列作为禁忌搜索算法的初始解。

2. 禁忌搜索算法优化：以Neh算法得到的初始解为起点，运用禁忌搜索算法进行进一步的优化，在搜索过程中不断更新禁忌表和历史最优解。

3. 输出结果：当禁忌搜索算法满足终止条件后，输出最终的历史最优解，即作业在机器上的最佳执行顺序，同时记录对应的最小总加工时间。

六、实验结果与分析

（一）实验设置

为了验证基于Neh算法和禁忌搜索算法的PFSP求解方法的有效性，设计以下实验。实验环境为[具体计算机硬件和软件环境]。

生成不同规模的PFSP实例，设置作业数量 nn 分别为 10,20,3010,20,30，机器数量 mm 分别为 5,105,10。对于每个实例，运行基于Neh算法和禁忌搜索算法的求解程序10次，记录每次得到的总加工时间 CmaxCmax​，并计算平均值和标准差。实际以运行结果为准。

（三）结果分析

从实验结果可以看出，随着作业数量 nn 和机器数量 mm 的增加，平均 CmaxCmax​ 总体呈上升趋势，这符合PFSP问题复杂度增加的预期。同时，标准差相对较小，说明算法具有较好的稳定性。

与单独使用Neh算法或禁忌搜索算法的结果进行对比（假设已有相关对比数据），可以发现基于Neh算法和禁忌搜索算法相结合的方法能够得到更优的总加工时间，证明了该方法在解决PFSP问题上的有效性和优势。

七、结论

本文对排列流车间调度问题（PFSP）进行了深入研究，详细阐述了Neh算法和禁忌搜索算法的基本思想、步骤，并将两者相结合用于求解PFSP问题。通过实验结果表明，该方法在不同规模的PFSP实例中都能有效地找到较优的作业执行顺序，最小化总加工时间，且具有较好的稳定性。未来的研究可以进一步探索更有效的邻域搜索策略和禁忌表更新方式，以进一步提高算法的性能，同时考虑将该方法应用于更复杂的实际生产调度场景中。

📚2 运行结果

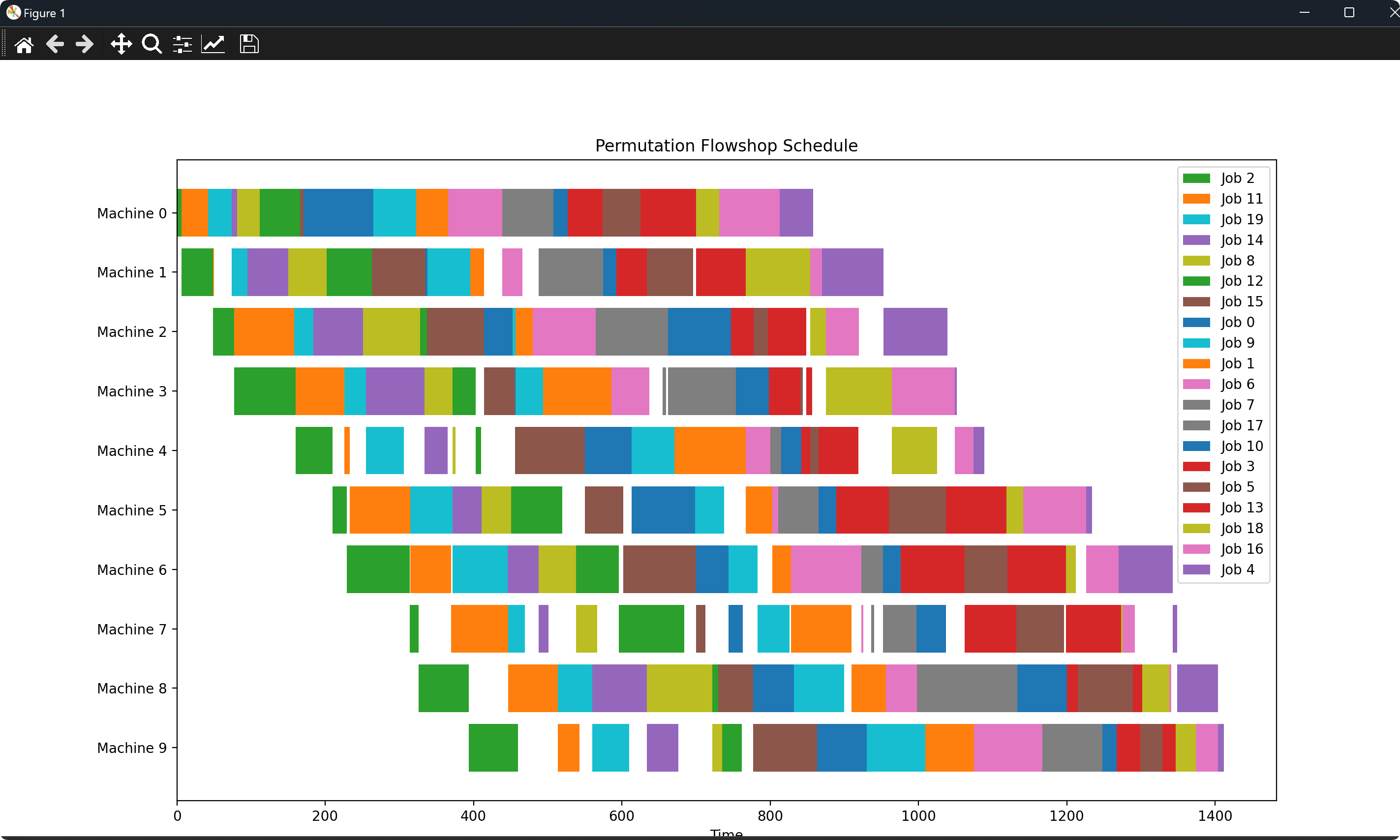
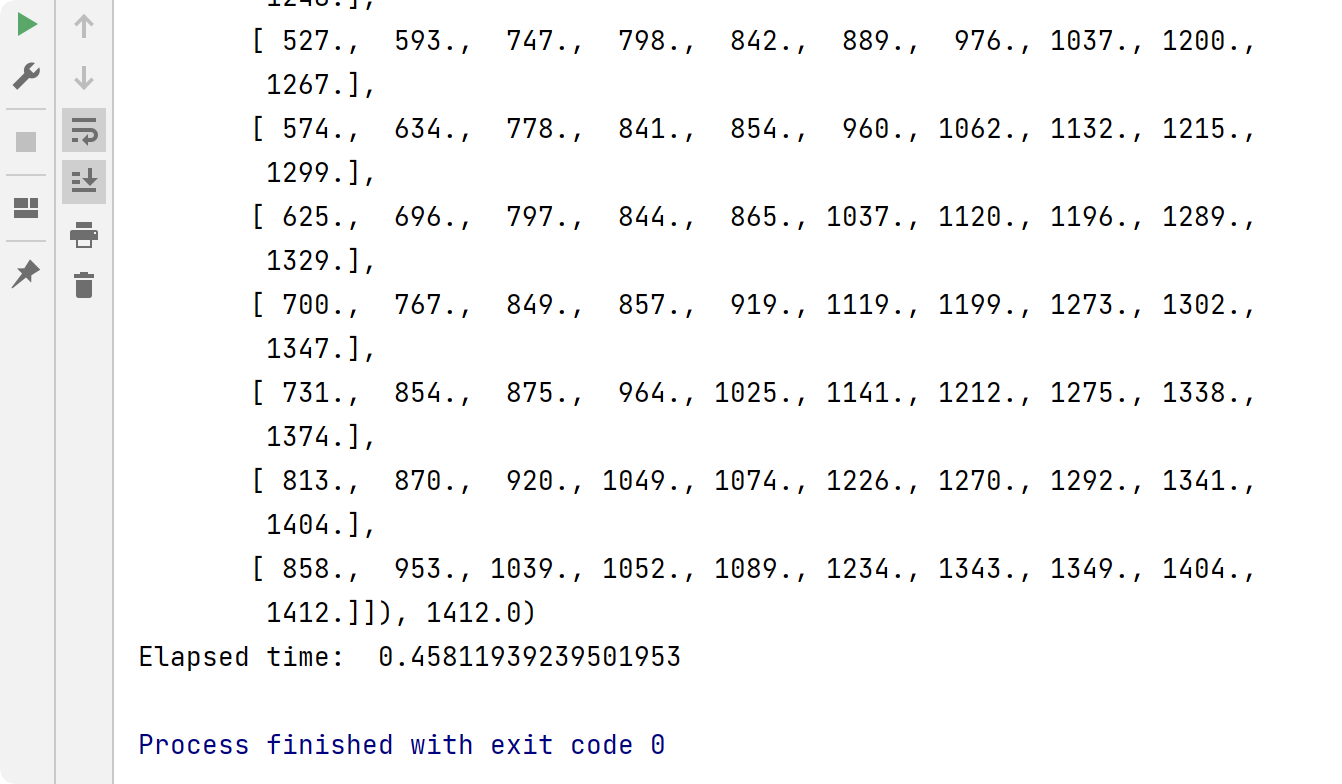
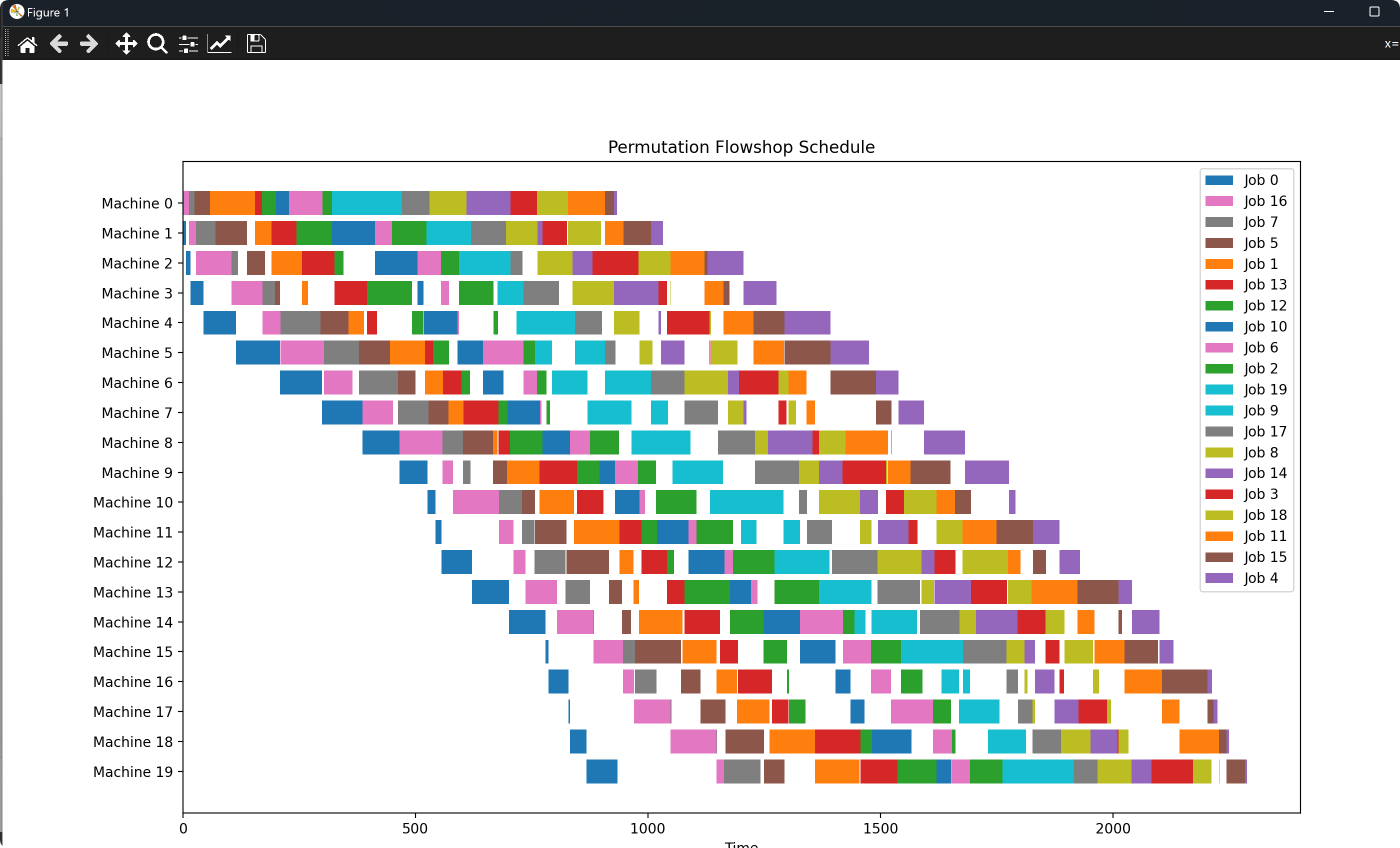
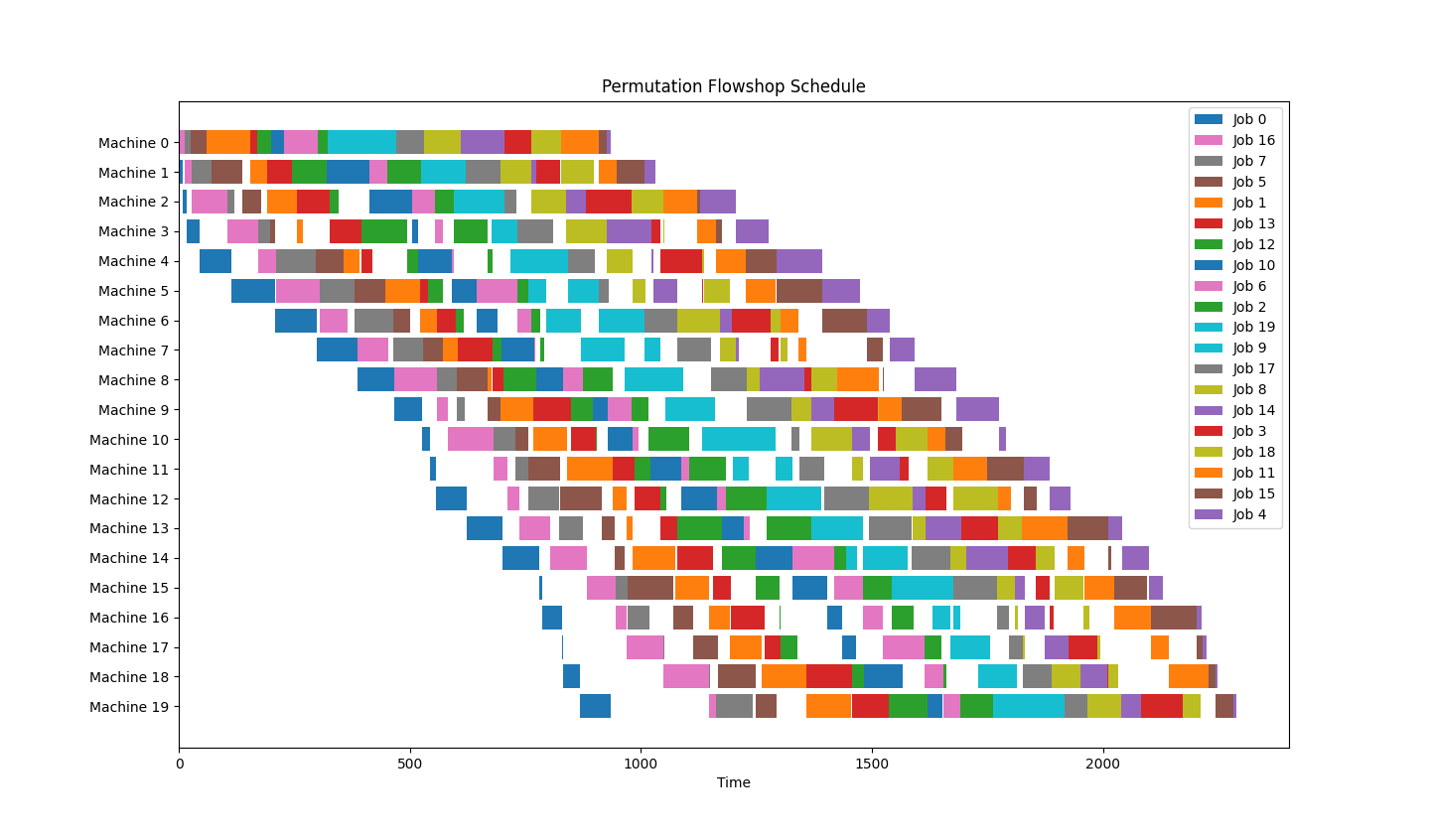
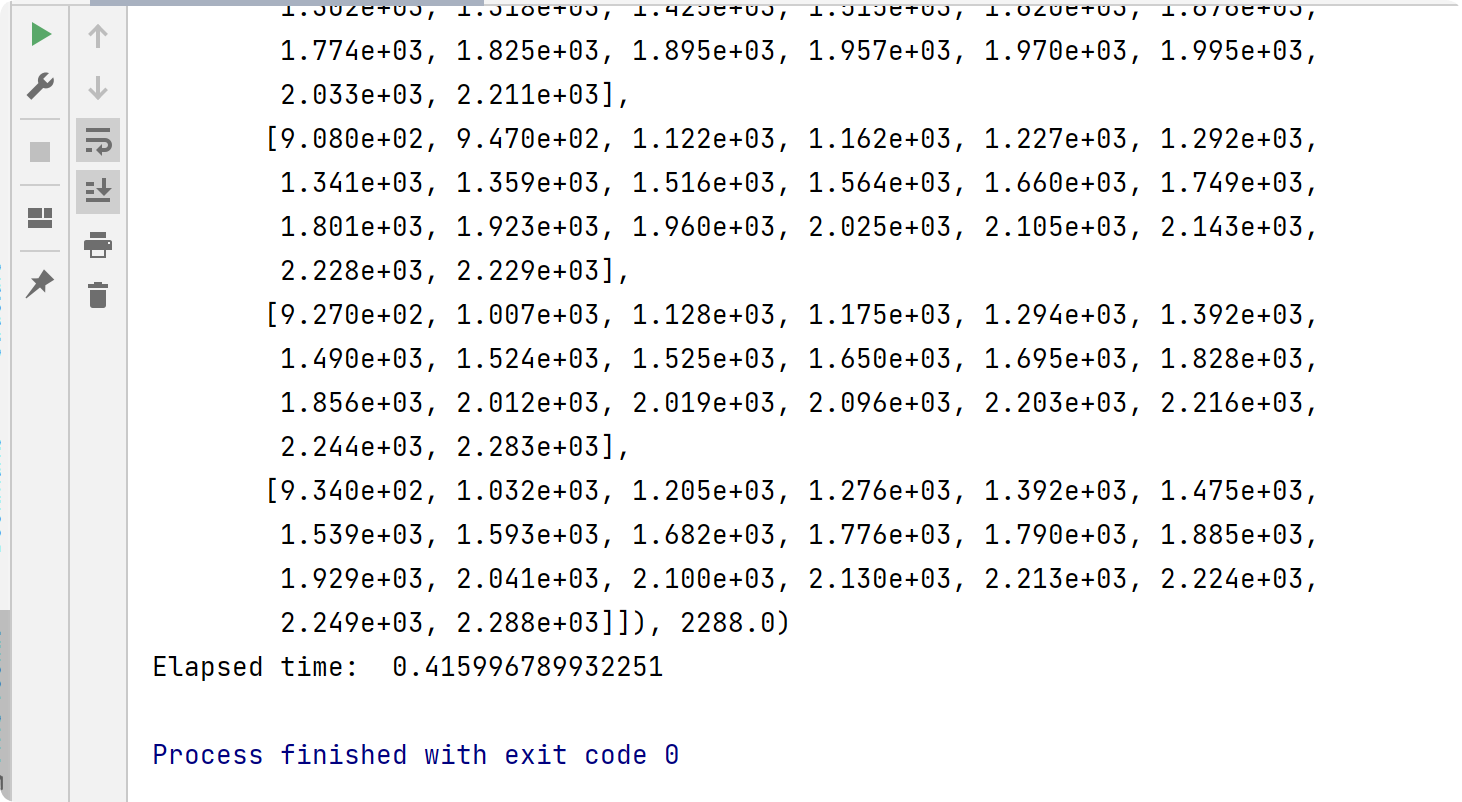
部分代码：

#############################################
#               NEH Algorithm               #
#############################################
def processing_time(num_jobs, num_machines, p_time):
    """
        STEP-1: Calculate the total time of each Job, in all Machines
    """
    descending_job_order = []
    total_times = []
    for j in range(num_jobs):
        sum = 0
        total_times_row = []
        for m in range(num_machines):
            sum = sum + p_time[j,m]
            total_times_row.append(p_time[j,m])
        total_times.append(total_times_row)
        descending_job_order.append((sum,j,total_times[j]))

    """
        STEP-2: Order the list in descending order
    """
    descending_job_order.sort(reverse=True)
    return descending_job_order

def order(num_jobs, num_machines, p_time): 
    descending_job_order = processing_time(num_jobs, num_machines, p_time) 
    job_order = []
    for j in range(num_jobs):
        # Insert in list -job_order- only the jobs
        job_order.append(descending_job_order[j][1])

🎉3 参考文献 

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。(文章内容仅供参考，具体效果以运行结果为准)

[1]张雨晨,熊福力.一种用于PFSP节能优化的混合禁忌搜索算法[J].计算机测量与控制, 2020, 028(012):166-171

[2]张雨晨,熊福力.一种用于PFSP节能优化的混合禁忌搜索算法[J].  2020.DOI:10.16526/j.cnki.11-4762/tp.2020.12.035.

🌈4 Python代码实现

资料获取，更多粉丝福利，MATLAB|Simulink|Python资源获取