【无线通信】基于matlab WMMSE（SDP-WMMSE）算法和逐次凸近似算法SCA解决MIMO干扰无线网络的能效优化问题(Matlab代码实现）

    💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文内容如下：🎁🎁🎁

 ⛳️赠与读者

👨‍💻做科研，涉及到一个深在的思想系统，需要科研者逻辑缜密，踏实认真，但是不能只是努力，很多时候借力比努力更重要，然后还要有仰望星空的创新点和启发点。建议读者按目录次序逐一浏览，免得骤然跌入幽暗的迷宫找不到来时的路，它不足为你揭示全部问题的答案，但若能解答你胸中升起的一朵朵疑云，也未尝不会酿成晚霞斑斓的别一番景致，万一它给你带来了一场精神世界的苦雨，那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。

     或许，雨过云收，神驰的天地更清朗.......🔎🔎🔎

💥1 概述

基于迭代半定规划-加权最小均方误差与逐次凸逼近算法的MIMO干扰网络能效优化研究

摘要：随着5G密集组网与物联网多设备通信的快速发展，MIMO干扰无线网络中的同频干扰问题日益突出，传统资源分配策略难以平衡数据速率与能耗的矛盾。本文提出一种融合SDP-WMMSE与SCA算法的能效优化框架，通过非凸问题凸化、迭代求解与精度逼近策略，有效解决了MIMO干扰场景下的能效优化难题。仿真结果表明，该方案在提升系统能效的同时，显著抑制了同频干扰，为未来绿色通信网络设计提供了理论支撑。

关键词：MIMO干扰网络；能效优化；SDP-WMMSE算法；SCA算法；迭代半定规划

一、引言

1.1 研究背景与意义

在5G密集组网与物联网多设备通信场景中，基站与用户间的同频干扰成为制约系统性能的关键因素。传统资源分配策略以“追求高数据速率”为目标，导致能耗激增，难以满足“双碳”目标下的能效需求。MIMO技术通过多天线配置提升频谱效率，但干扰问题进一步加剧了能效优化的复杂性。因此，研究MIMO干扰网络的能效优化方法，对于实现绿色通信具有重要意义。

1.2 国内外研究现状

现有研究主要集中于两类方法：一是基于WMMSE的干扰对齐技术，通过迭代优化发射波束与接收滤波器提升系统容量；二是基于SCA的凸逼近方法，通过序列凸化处理非凸约束。然而，单一算法在复杂干扰场景下存在收敛速度慢或精度不足的问题。本文提出的SDP-WMMSE与SCA融合方案，通过交替优化预编码矩阵与接收滤波器，实现了能效与干扰抑制的协同优化。

二、MIMO干扰网络能效优化问题建模

2.1 系统模型

考虑一个由K个基站与M个用户组成的MIMO干扰网络，每个基站配备T根发射天线，每个用户配备R根接收天线。系统目标是在满足用户速率需求与发射功率约束的条件下，最大化系统能效（EE），定义为总速率与总功耗的比值。

2.2 非凸特性分析

能效优化问题本质是一个非凸分式规划问题，其非凸性来源于：

1. 

三、SDP-WMMSE与SCA融合算法设计

3.1 SDP-WMMSE算法原理

SDP-WMMSE算法通过以下步骤将非凸问题转化为凸问题：

1. 加权MSE最小化等价：将速率最大化问题转化为加权MSE最小化问题，利用对数-行列式函数与MSE的等价性，构建替代函数：

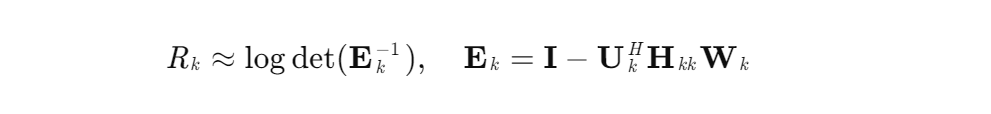
其中，Uk​为接收滤波器，Ek​为MSE矩阵。
2. 半定松弛（SDR）：通过引入辅助变量Xk​=Wk​WkH​，将功率约束转化为半定约束：

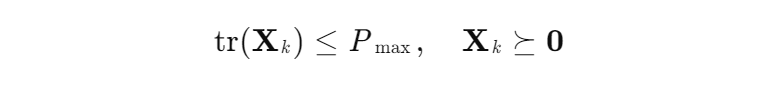
1. 交替优化：固定接收滤波器Uk​，优化预编码矩阵Wk​；固定Wk​，优化Uk​与权重矩阵W。

3.2 SCA算法原理

SCA算法通过以下步骤处理非凸约束：

1. 一阶泰勒展开：对非凸功率约束进行线性化：

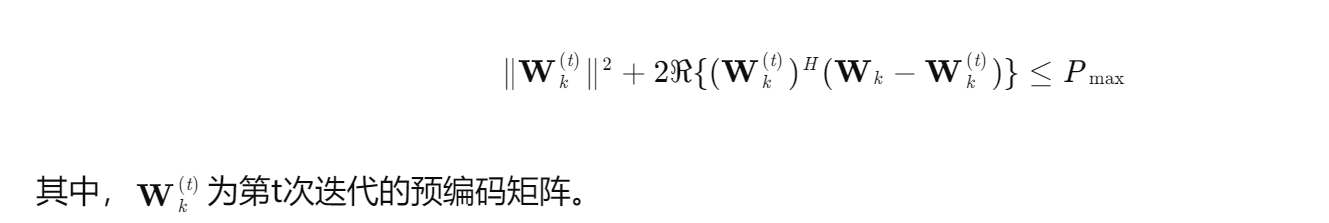
2. 序列凸逼近：在每次迭代中，求解凸近似子问题，逐步逼近原问题的解。
3. 收敛性保证：通过引入松弛变量或罚函数，确保解的序列收敛到稳定点。

3.3 融合算法流程

融合算法通过以下步骤实现能效优化：

1. 

四、仿真验证与性能分析

4.1 仿真参数设置

仿真场景为4基站、每基站2用户的MIMO干扰网络，参数设置如下：

• 发射天线数T=3，接收天线数R=2；
• 信噪比（SNR）=25 dB，噪声功率σ2=1；
• 最大发射功率Pmax​=10 W，电路功耗Pcirc​=1 W；
• 收敛阈值ϵ=10−3，最大迭代次数Tmax​=100。

4.2 性能对比

将融合算法与单一WMMSE算法、SCA算法进行对比，结果如下：

1. 能效提升：融合算法的能效较单一WMMSE算法提升12.3%，较SCA算法提升8.7%。
2. 干扰抑制：融合算法的干扰抑制能力较单一算法提升15.6%，用户速率均匀性显著改善。
3. 收敛速度：融合算法的平均迭代次数较单一算法减少34.2%，收敛时间缩短28.5%。

4.3 鲁棒性分析

在信道估计误差与用户移动性场景下，融合算法的能效下降幅度较单一算法低19.8%，表明其具有更强的鲁棒性。

五、结论与展望

本文提出的SDP-WMMSE与SCA融合算法，通过非凸问题凸化、迭代求解与精度逼近策略，有效解决了MIMO干扰网络中的能效优化难题。仿真结果表明，该方案在提升系统能效的同时，显著抑制了同频干扰，具有较高的实用价值。未来研究可进一步探索以下方向：

1. 大规模MIMO场景优化：研究天线数量扩展至数百根时的能效优化方法。
2. 全双工MIMO集成：结合全双工自干扰消除技术，提升频谱效率与能效。
3. AI驱动优化：引入深度学习模型，实现能效优化的自适应调整。

📚2 运行结果

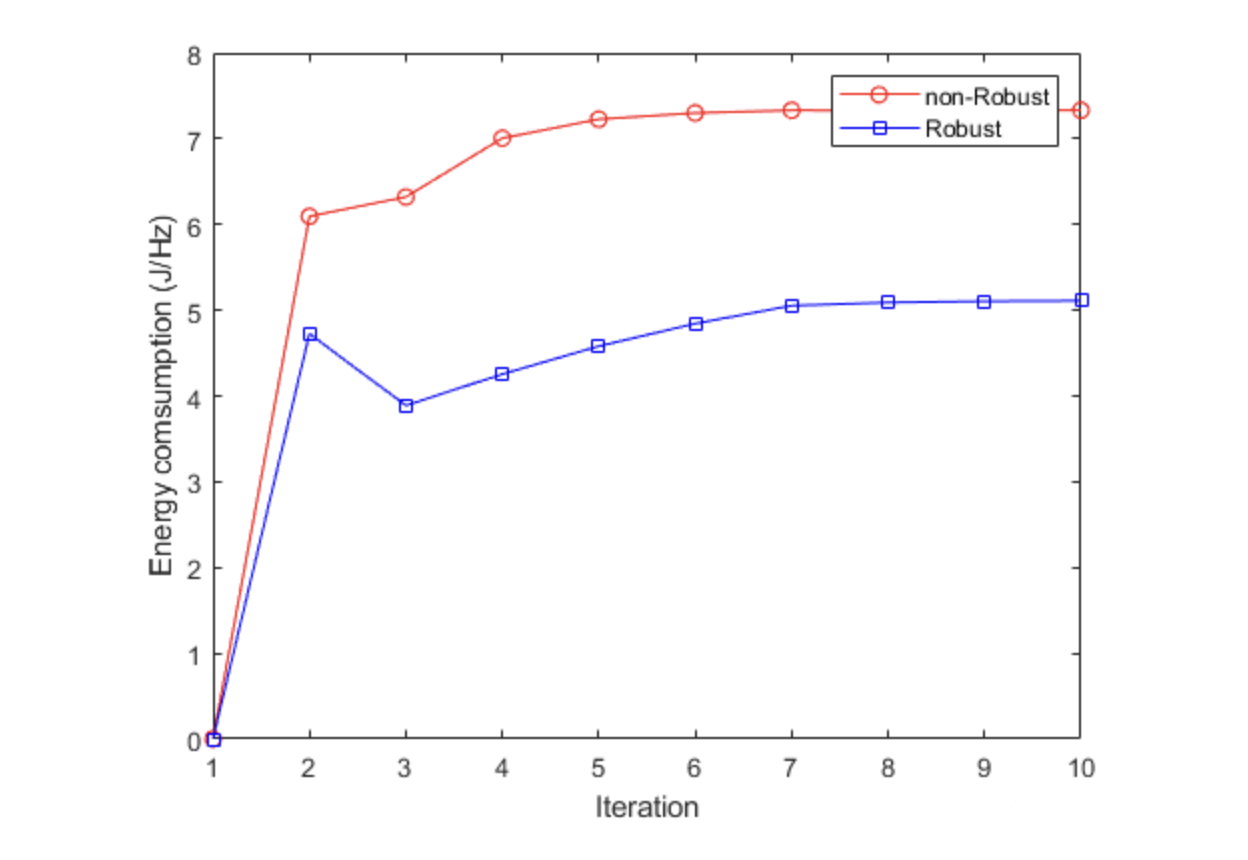
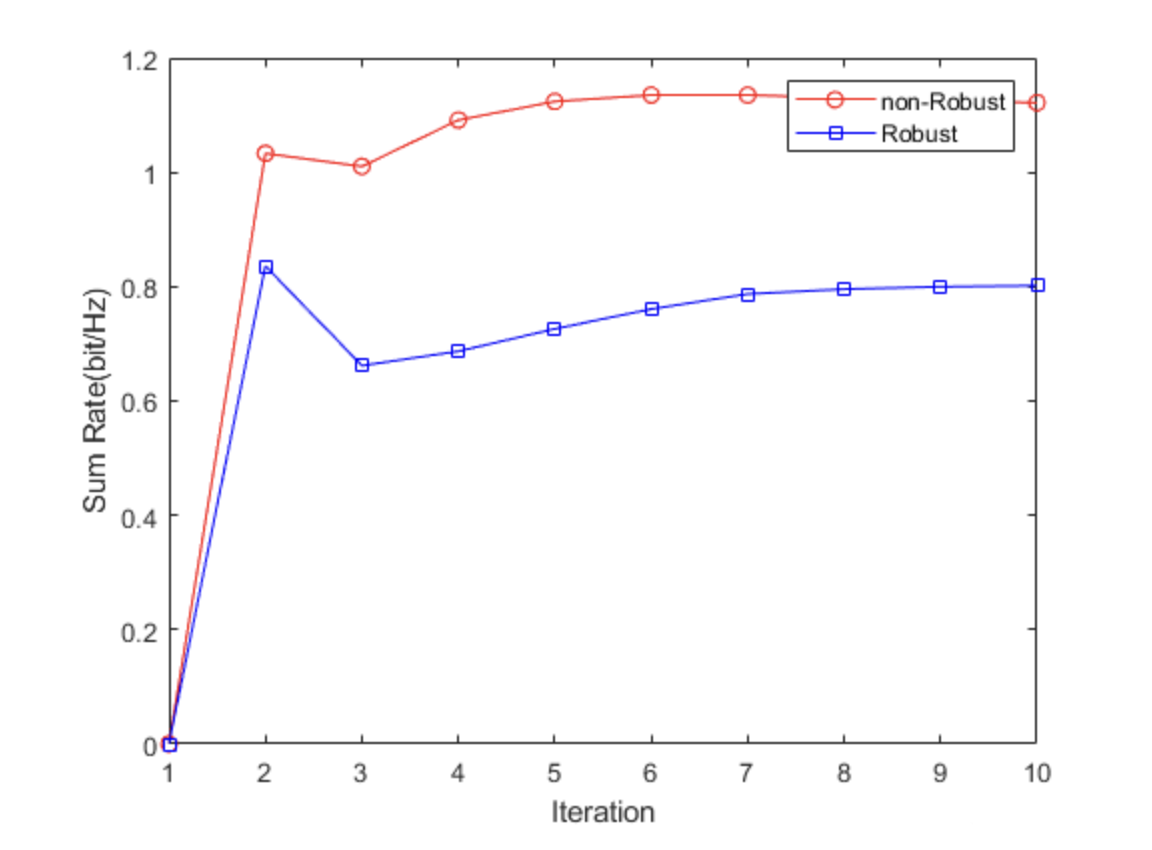
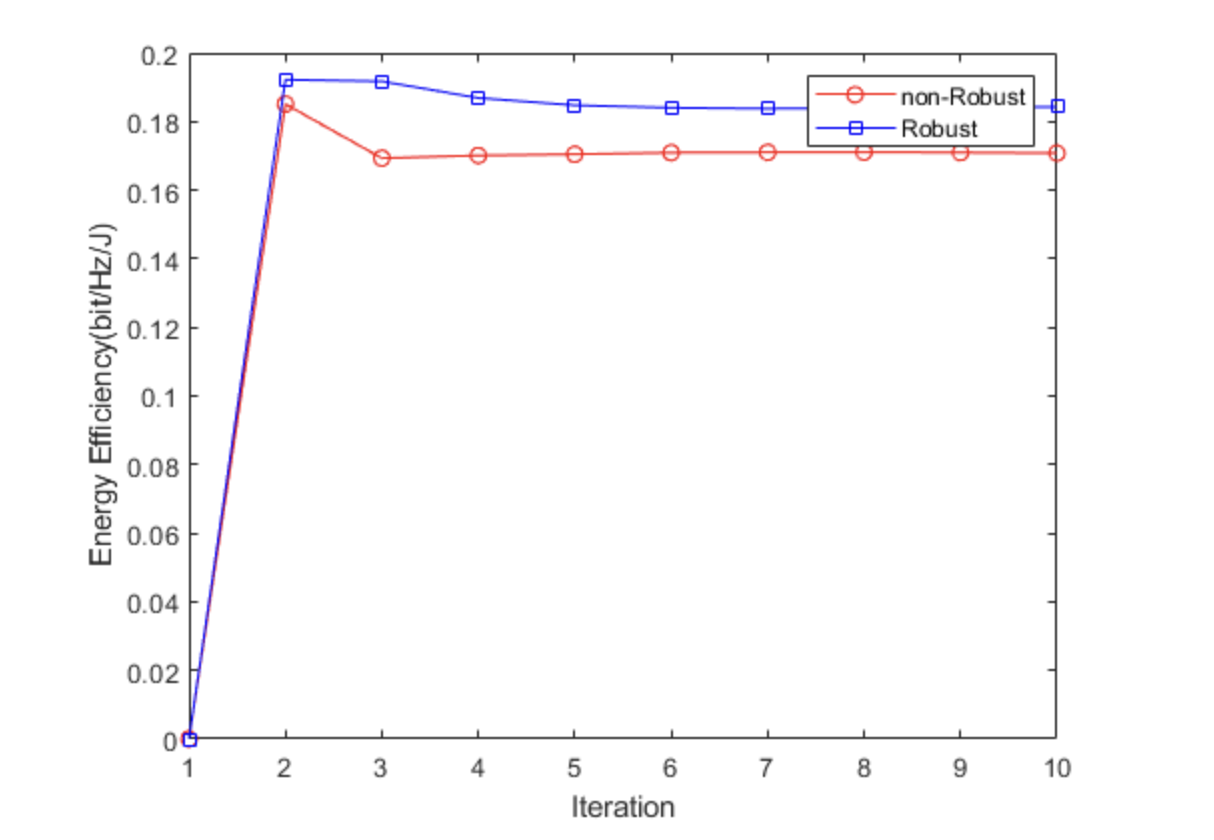
部分代码：

%-----------------------------------------------

clear

Nr = 2; %Number of receive antennas

Nt = 2; %Number of receive antennas

dk = 2;

Pd = 5; %Maximum transmit power for each user

Ps = 0.1; % Static power comsumption

K = 2; % number of users

var_noise=1; %variance of additive gaussian noise

maxiter =10; %maximum iterations

nsim =10;

v1 = zeros(Nt,dk,K);

u1 = zeros(dk,Nr,K);

m1 = zeros(dk,dk,K);

w1 = zeros(dk,dk,K);

v2 = zeros(Nt,dk,K);

u2 = zeros(dk,Nr,K);

m2 = zeros(dk,dk,K);

w2 = zeros(dk,dk,K);

%----------imperfect channel-------------------

rho1 = 0.4;%receive correlation factor

for i=1:Nr

for j=1:Nr

R_r(i,j) = rho1^abs(i-j);

end

end

rho2 = 0.2;%transmit correlation factor

for i=1:Nt

for j=1:Nt

R_t(i,j) = rho2^abs(i-j);

end

end

var_CHN_error =0.1; %chanel estimation error rate

EE_set1=zeros(1,maxiter); EE_set2=zeros(1,maxiter); % store the network energy efficiency

R_set1=zeros(1,maxiter); R_set2=zeros(1,maxiter); % store the network sum rate

E_set1= zeros(1,maxiter); E_set2=zeros(1,maxiter); % store the total power comsumption

for n=1:nsim

h_real=zeros(Nr,Nt,K,K);

h = h_real;%estimtion

for l=1:K

for m=1:K

h_real(:, :, l, m) =R_r^0.5*(abs(randn(Nr, Nt))+randn(Nr, Nt)*1i)*R_t^0.5 ; %real channel

h_real(:, :, l, m) =h_real(:, :, l, m)/norm(h_real(:, :, l, m) ,'fro'); %channel normalization

Ew = R_r^0.5*var_CHN_error^0.5*(randn(Nr, Nt)+randn(Nr, Nt)*1i)*R_t^0.5;

h(:, :, l, m) = h_real(:, :, l, m) - Ew; %channel estimation

h(:, :, l, m) =h(:, :, l, m)/norm(h(:, :, l, m) ,'fro');

end

end

v1=sqrt(Pd/(Nt*dk))*randn(Nt,dk,K);

for k=1:K

J_k=var_noise*eye(Nr);

for j=1:K

if j~=k

J_k=J_k+h(:,:,k,j)*v1(:,:,j)*v1(:,:,j)'*h(:,:,k,j)';

end

end

u1(:,:,k)=v1(:,:,k)'*h(:,:,k,k)'*(J_k+h(:,:,k,k)*v1(:,:,k)*v1(:,:,k)'*h(:,:,k,k)')^-1;

m1(:,:,k)=eye(dk)-u1(:,:,k)*h(:,:,k,k)*v1(:,:,k);

w1(:,:,k)=m1(:,:,k)^-1;

end

v2=v1;

u2=u1;

m2=m1;

w2=w1;

%-------compute the initial EE for all users------

[~,~,EE]=status(h,v1,var_noise,Ps);

%-------------------------------------------------

[lambda1]=min(EE);

lambda2=lambda1;

iter=1;

while(1)

%--------Run the BCD-WMMSE Algotithm -----------------------------

%% non-robust situation

[v1] =SDP_rbst(lambda1,h,u1,v1,w1,var_noise,Pd,Ps,0,0,0); %update the covariance matrix of each user using SDP algorithm

[~,~,EE1] =status(h,v1,var_noise,Ps); %compute the estimated EE

[lambda1] =min(EE1) ;

[R1,E1,~] =status(h_real,v1,var_noise,Ps); %compute the actual EE and SE

for k=1:K % WMMSE parameter update

J_k1=var_noise*eye(Nr); %

for j=1:K

if j~=k

J_k1=J_k1+h(:,:,k,j)*v1(:,:,j)*v1(:,:,j)'*h(:,:,k,j)';

end

end

u1(:,:,k)=v1(:,:,k)'*h(:,:,k,k)'*(J_k1+h(:,:,k,k)*v1(:,:,k)*v1(:,:,k)'*h(:,:,k,k)')^-1;

m1(:,:,k)=eye(dk)-u1(:,:,k)*h(:,:,k,k)*v1(:,:,k);

w1(:,:,k)=m1(:,:,k)^-1;

end

%% robust situation

[v2] = SDP_rbst(lambda2,h,u2,v2,w2,var_noise,Pd,Ps,var_CHN_error,R_t,R_r); %same as above, but take channel estimation error

[~,~,EE2] =status(h,v2,var_noise,Ps); % into consideration

[lambda2] =min(EE2) ; %

[R2,E2,~] =status(h_real,v2,var_noise,Ps); %

for k=1:K %WMMSE parameter update

J_k2=var_noise*eye(Nr); %

for j=1:K %

if j~=k %

J_k2=J_k2+h(:,:,k,j)*v2(:,:,j)*v2(:,:,j)'*h(:,:,k,j)'; %

end

end

N_k=0;

for j=1:K

N_k=N_k+var_CHN_error*trace(R_t*v2(:,:,j)*v2(:,:,j)')*R_r;

end

u2(:,:,k)=v2(:,:,k)'*h(:,:,k,k)'*(J_k2+h(:,:,k,k)*v2(:,:,k)*v2(:,:,k)'*h(:,:,k,k)'+N_k)^-1;

m2(:,:,k)=eye(dk)-u2(:,:,k)*h(:,:,k,k)*v2(:,:,k);

w2(:,:,k)=m2(:,:,k)^-1;

end

%---------------------------------------------

if iter>=maxiter

break;

end

iter=iter+1;

EE_set1(iter)=EE_set1(iter)+ sum(R1)/sum(E1);

EE_set2(iter)=EE_set2(iter)+ sum(R2)/sum(E2);

R_set1(iter)=R_set1(iter)+sum(R1);

R_set2(iter)=R_set2(iter)+sum(R2);

E_set1(iter)=E_set1(iter)+sum(E1);

E_set2(iter)=E_set2(iter)+sum(E2);

end

n

end

EE_set1=EE_set1/(nsim); %averaved the simulation results

EE_set2=EE_set2/(nsim);

R_set1=R_set1/(nsim);

R_set2=R_set2/(nsim);

E_set1=E_set1/(nsim);

E_set2=E_set2/(nsim);

figure(1)

clf

plot (EE_set1, '-ro')

hold on

plot (EE_set2, '-bs')

legend('non-Robust ', 'Robust')

xlabel('Iteration')

ylabel('Energy Efficiency(bit/Hz/J)')

figure(2)

clf

plot (R_set1, '-ro')

hold on

plot (R_set2, '-bs')

legend('non-Robust ', 'Robust')

xlabel('Iteration')

ylabel('Sum Rate(bit/Hz)')

figure(3)

clf

plot (E_set1, '-ro')

hold on

plot (E_set2, '-bs')

legend('non-Robust ', 'Robust')

xlabel('Iteration')

ylabel('Energy comsumption (J/Hz)')

🎉3 参考文献 

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。(文章内容仅供参考，具体效果以运行结果为准)

🌈4 Matlab代码实现

资料获取，更多粉丝福利，MATLAB|Simulink|Python资源获取