【全局灵敏性】【蒙特卡洛敏感性指数估计和多精度策略】基于方差的全局敏感性分析（Matlab代码实现）

最新推荐文章于 2025-12-03 22:33:21 发布

原创最新推荐文章于 2025-12-03 22:33:21 发布 · 763 阅读

16 ·

CC 4.0 BY-SA版权

文章标签：

#matlab #python #人工智能 #支持向量机

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

💥1 概述

当模型具有不确定的输入时，模型的输出也是不确定的。基于方差的全局敏感性分析通过将总方差分解为由每个不确定的输入和输入之间的相互作用导致的方差的百分比，来量化每个不确定输入对输出的相对影响。例如，Ishigami函数具有3个随机输入Z1、Z2和Z3，它们分布在区间[-𝜋,𝜋]上：

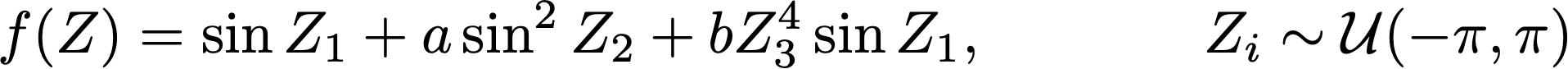
因此，Ishigami函数的方差可以分解为由单独的输入1、单独的输入2、单独的输入3以及输入1和2、输入1和3、输入2和3之间的相互作用，或者由所有三个输入之间的相互作用所引起的方差分量。这种分解被称为方差分析（ANOVA）分解，相当于将方差“馅饼”分解成不同的片段。对于上述的Ishigami函数（其中a=5，b=0.1），有40%的方差归因于Z1单独，29%的方差归因于Z2单独，31%的方差归因于Z1和Z3之间的相互作用。因此，方差“饼图”如下所示：

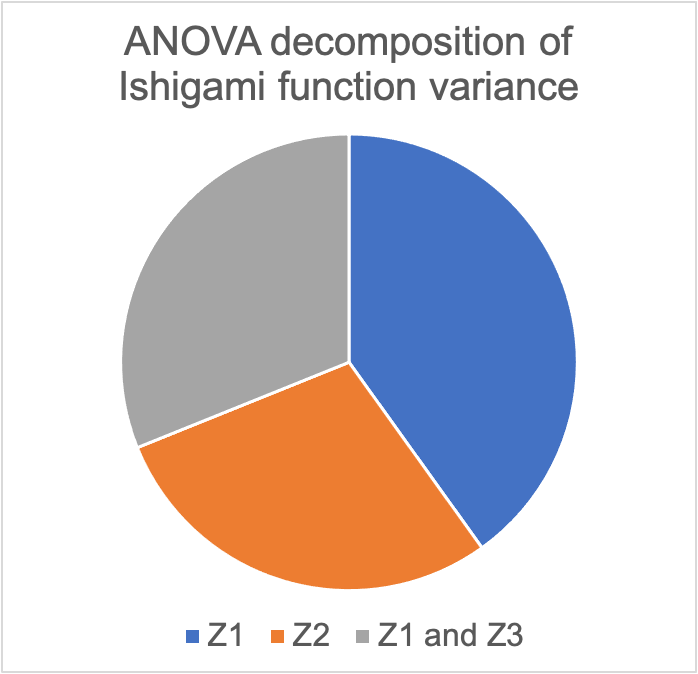
饼图，40%标记为Z1，29%标记为Z2，31%标记为Z1和Z3

基于方差的全局敏感性分析研究

全局敏感性指数量化了方差分解中每个输入的贡献。对于给定的输入，有两种不同的全局敏感性指数：

主效应敏感性指数，表示可以归因于该输入独自的方差百分比，即不考虑与其他输入之间的相互作用导致的影响，
总效应敏感性指数，表示受该输入影响的总方差百分比，包括仅由该输入产生的效应以及由该输入和其他输入产生的效应。
一般来说，所有输入的主效应敏感性指数之和为1或小于1，而所有输入的总效应敏感性指数之和为1或大于1。例如，在上述的Ishigami函数示例中，Z1、Z2和Z3的主效应敏感性指数分别为0.40、0.29和0，而总效应敏感性指数分别为0.71、0.29和0.31。

蒙特卡洛敏感性指数估计和多精度策略
主要效应和总效应敏感性指数可以使用蒙特卡洛估计进行估计。对于d个输入来估计主要和总效应敏感性指数，每个蒙特卡洛样本需要(d+2)个函数评估，因此当模型昂贵且d较大时，蒙特卡洛估计可能非常昂贵。我们提出多精度估计器，它结合了使用昂贵模型计算的少量高精度样本和使用更便宜的代理模型计算的许多低精度样本，以在固定的计算预算下提供比仅使用高精度模型更低方差的估计，同时保持高精度估计的准确性。

一、全局敏感性分析（GSA）的基本概念与核心方法

全局敏感性分析（Global Sensitivity Analysis, GSA）旨在量化输入参数的不确定性对模型输出的整体影响，特别适用于非线性、高维且参数间存在复杂交互作用的模型。与局部敏感性分析（仅关注参数在名义值附近的变化）不同，GSA通过考虑输入参数在其整个分布域内的变化，全面评估其对输出不确定性的贡献。

核心方法分类：

基于方差的GSA（如Sobol方法）：通过方差分解量化参数及其交互作用对输出方差的贡献。
矩独立GSA：基于概率密度函数或累积分布函数分析参数的影响。
基本效应法（如Morris方法）：通过参数空间遍历快速筛选重要参数。

其中，基于方差的Sobol方法因其数学严谨性和对交互作用的显式建模，成为应用最广泛的方法。

二、基于方差的Sobol方法数学模型

Sobol方法的核心是将模型输出方差分解为单个参数及其组合的贡献，具体步骤如下：

三、蒙特卡洛敏感性指数估计的实现

蒙特卡洛方法是估计Sobol指数的常用手段，其核心是通过随机采样生成输入输出样本，并计算方差贡献。

关键步骤：

样本生成：
- 使用拉丁超立方抽样（LHS）或Saltelli序列生成两套输入矩阵 A 和 B，并通过交叉组合构造子样本集。
- 总样本量为 N=(d+2)×n，其中 d 为参数数量，n 为基样本数。
指数计算：
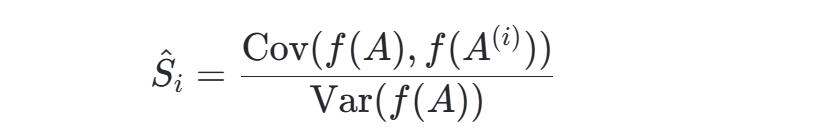
- 一阶指数估计公式：

其中 A(i)表示将矩阵 A的第 i 列替换为 B 的对应列。

总效应指数通过反向方差法或双循环蒙特卡洛实现。

置信区间与误差控制：
- 采用自助法（Bootstrap）或重复实验估计指数的不确定性。
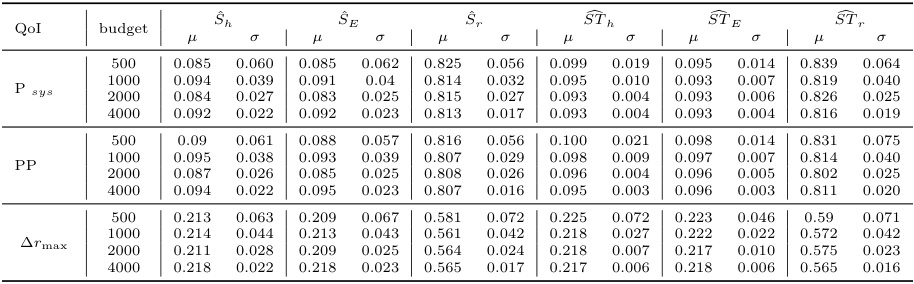
- 例如，表17显示在预算4000次模拟时，Δr_max的总效应指数均值为0.218，标准偏差为0.022，表明估计的稳定性。

优缺点：

优点：无需模型可导，适用于黑箱模型；可处理高维问题。
缺点：计算成本高，尤其对计算密集型模型；收敛速度慢（O(1/N)O(1/N)）。

四、多精度策略的应用场景与实现

多精度策略通过结合不同计算成本的模型（高保真与低保真）来降低计算开销，同时保持估计精度。

典型方法：

多保真蒙特卡洛（MFMC）：
- 利用低保真模型生成大量廉价样本，结合少量高保真样本进行校正。
- 例如，在颈动脉血流动力学模型中，将少量3D仿真与大量1D简化模型结合，实现方差缩减。
多项式混沌展开（PCE）：
- 构建低保真代理模型（如低阶PCE），加速Sobol指数计算。
- 多精度PCE通过校正项（如高保真与低保真残差）提升精度。
贝叶斯共克里金法：
- 融合多精度模型输出，通过贝叶斯框架估计敏感性指数。

案例研究：

化学反应网络：使用确定性低保真模型替代随机高保真模型，验证交互作用的一致性。
金融风险模型：通过多级蒙特卡洛（MLMC）分层抽样，平衡计算成本与精度。

五、复杂模型中的蒙特卡洛与多精度策略结合案例

步骤示例：

模型分层：
- 高保真模型（HF）：计算成本高，精度高。
- 低保真模型（LF）：计算快，精度较低。
样本分配：
- 生成 NHFNHF 个HF样本和 NLFNLF 个LF样本，满足 NHF≪NLF。
校正与融合：
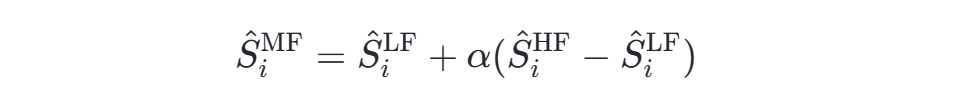
- 使用HF样本校准LF模型的偏差，构建混合估计器：

其中 αα 为校正系数。

结果验证：
- 如表17所示，双保真（1D/3D）估计器在预算2000时，总效应指数的标准偏差较单保真方法降低40%。

优势：

计算成本降低50%-80%，同时保持敏感性排序的一致性。
适用于高维工程模型（如风机叶片设计、核反应堆仿真）。

六、研究挑战与未来方向

高维问题：蒙特卡洛方法在参数维度增加时计算量呈指数增长，需结合稀疏采样或深度学习代理模型。
多输出模型：现有方法多为单输出设计，需发展基于主成分分析（PCA）或协方差分解的多输出GSA。
不确定性传播：多精度策略中低保真模型的误差传播机制需进一步量化。
实时性需求：面向在线决策的场景，需开发增量式GSA算法。

七、结论

基于方差的全局敏感性分析通过Sobol方法提供了参数影响的定量评估，蒙特卡洛估计与多精度策略的结合显著提升了复杂模型的分析效率。未来研究需在计算效率、多输出处理及误差控制方面进一步突破，以应对工程与科学模型日益增长的复杂度需求。

📚2 运行结果

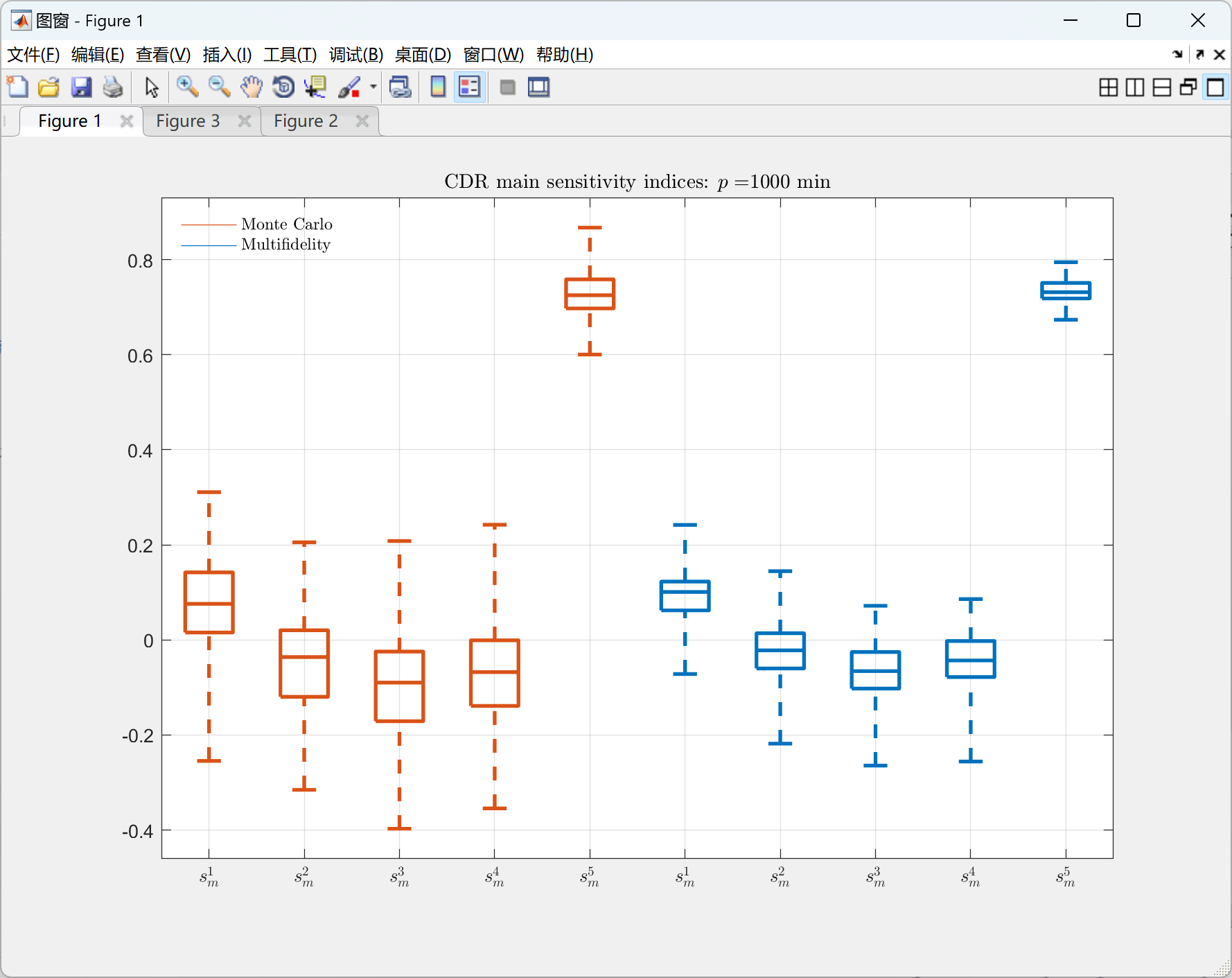
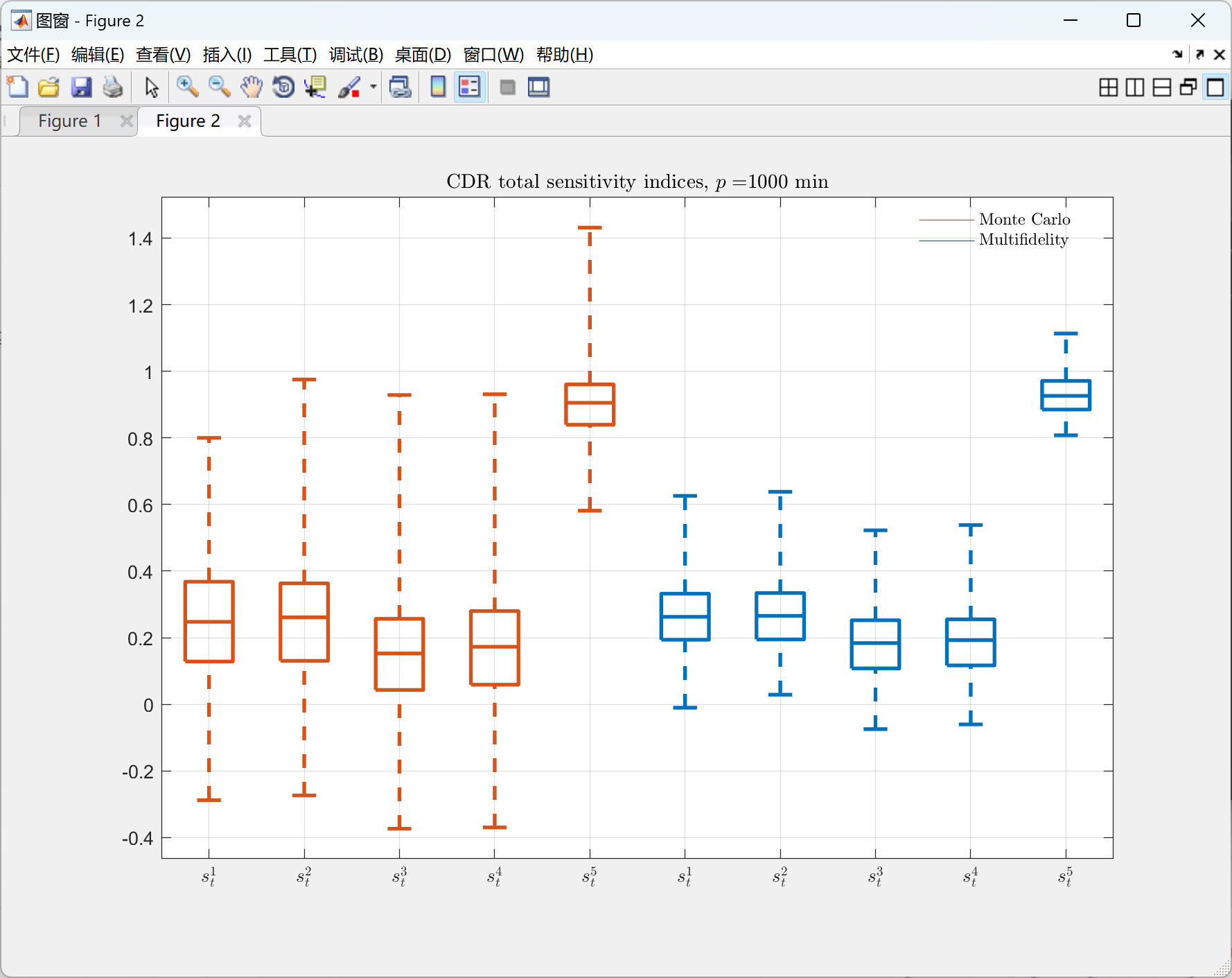
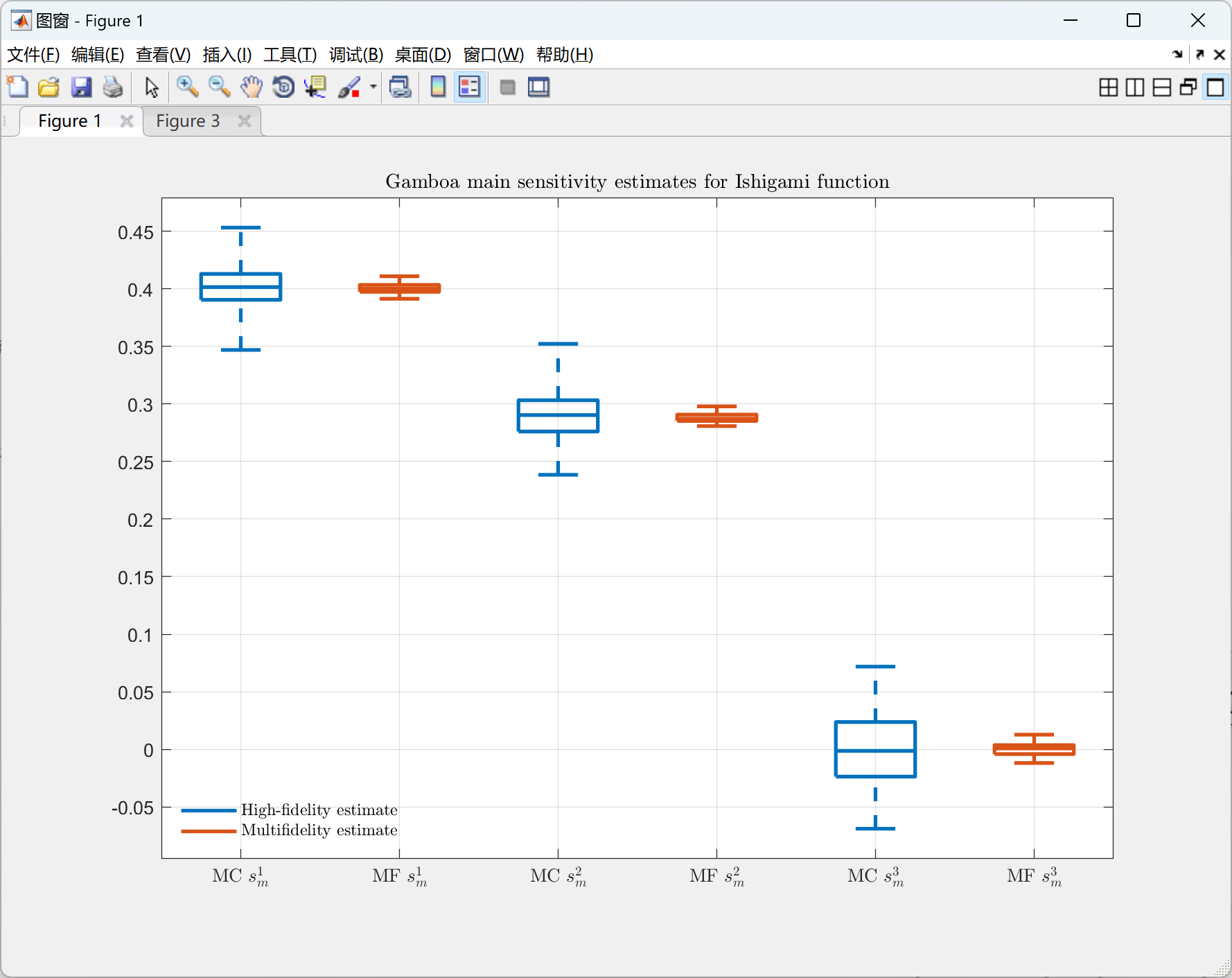
部分代码：

%% COMPUTE MULTIFIDELITY GLOBAL SENSITIVITY ANALYSIS REPLICATES
n_reps = 100; % number of replicates
avg = zeros(n_reps,2); vr = zeros(n_reps,2);
mc_sm = zeros(n_reps,d); mc_st = zeros(n_reps,d);
mf_sm = zeros(n_reps,d); mf_st = zeros(n_reps,d);

method = 'Gamboa';

for n = 1:n_reps

% call mfsobol.m with just the high-fidelity model to get Monte
% Carlo estimate
[sm,st,mu,sigsq] = mfsobol(fcns(1),d,w(1),stats,budget,vec(1),method);
avg(n,1) = mu;
vr(n,1) = sigsq;
mc_sm(n,:) = sm;
mc_st(n,:) = st;

% call mfsobol.m with full array of functions to get multifidelity
% estimates
[sm,st,mu,sigsq] = mfsobol(fcns,d,w,stats,budget,vec,method);
avg(n,2) = mu;
vr(n,2) = sigsq;
mf_sm(n,:) = sm;
mf_st(n,:) = st;
end

%% PLOT ESTIMATOR SPREAD
warning('off','MATLAB:legend:IgnoringExtraEntries')
blue = [0 0.4470 0.7410];
red = [0.8500 0.3250 0.0908];

% plot main effect sensitivity indices
figure(1); clf
h = boxplot([mc_sm(:,1), mf_sm(:,1), mc_sm(:,2), mf_sm(:,2), mc_sm(:,3), mf_sm(:,3)],...
'Colors',[blue; red; blue; red; blue; red],'Whisker',10,...
'labels',{'MC $s_m^1$','MF $s_m^1$','MC $s_m^2$','MF $s_m^2$','MC $s_m^3$','MF $s_m^3$'});
set(h,{'linew'},{2}); grid on
legend(flipud(findall(gca,'Tag','Box')), {'High-fidelity estimate','Multifidelity estimate'},...
'Location','SouthWest','interpreter','latex'); legend boxoff
bp = gca; bp.XAxis.TickLabelInterpreter = 'latex';
title([method,' main sensitivity estimates for Ishigami function'],'interpreter','latex')

if strcmp(method,'Owen') || strcmp(method,'Saltelli')
% plot total effect sensitivity indices
figure(2); clf
h = boxplot([mc_st(:,1), mf_st(:,1), mc_st(:,2), mf_st(:,2), mc_st(:,3), mf_st(:,3)],...
'Colors',[blue; red; blue; red; blue; red],'Whisker',10,...
'labels',{'MC $s_t^1$','MF $s_t^1$','MC $s_t^2$','MF $s_t^2$','MC $s_t^3$','MF $s_t^3$'});
set(h,{'linew'},{2}); grid on
hLegend = legend(flipud(findall(gca,'Tag','Box')), {'High-fidelity estimate','Multifidelity estimate'},...
'Location','NorthEast','interpreter','latex'); legend boxoff
bp = gca; bp.XAxis.TickLabelInterpreter = 'latex';
title([method,' total sensitivity estimates for Ishigami function'],'interpreter','latex')
end

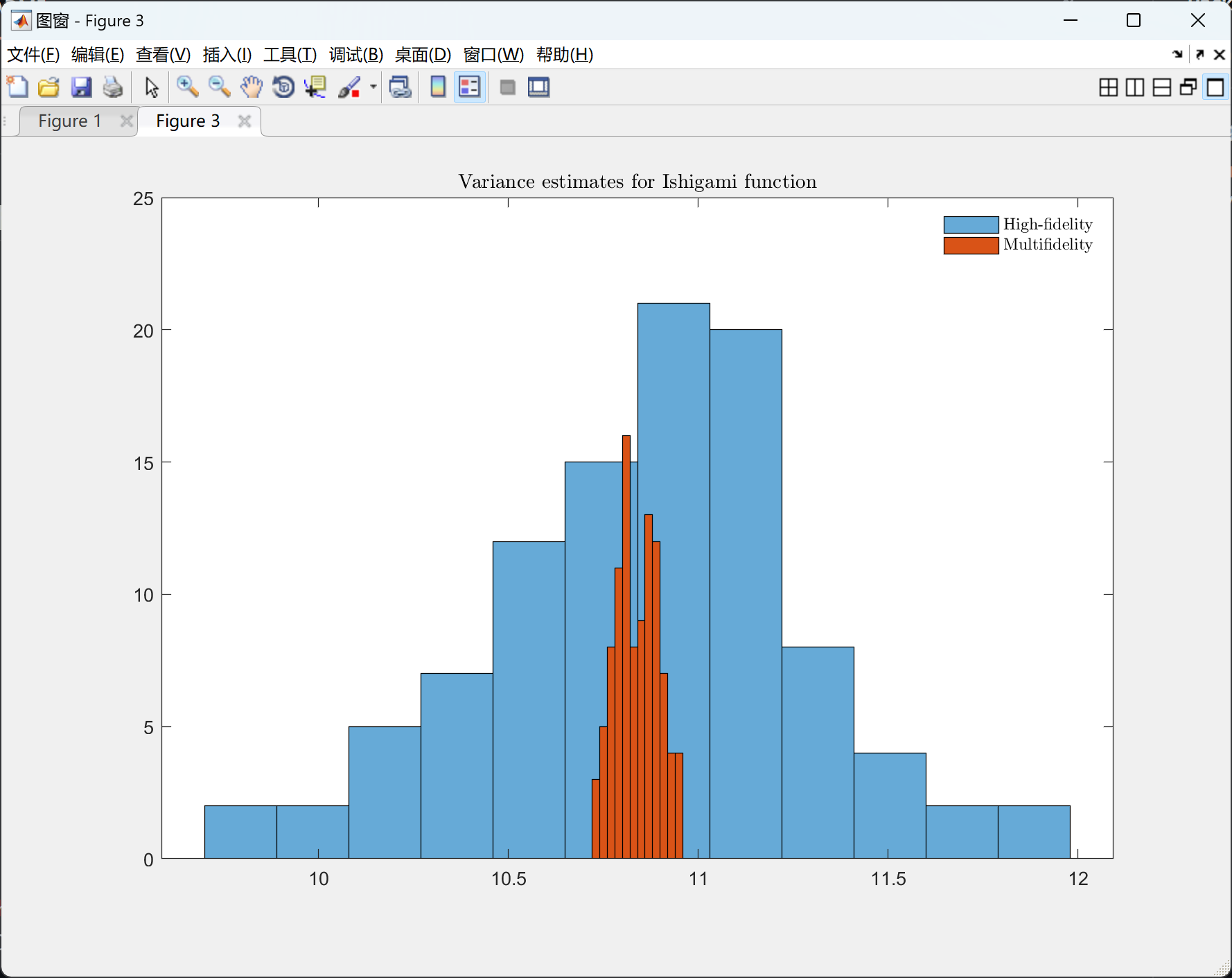
% plot variance estimates
figure(3); clf
histogram(vr(:,1),12,'facecolor',blue); hold on
histogram(vr(:,2),12,'facecolor',red,'facealpha',1)
legend({'High-fidelity','Multifidelity'},'interpreter','latex'); legend boxoff
title('Variance estimates for Ishigami function','interpreter','latex')